Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting

Abstract
본 연구는 시계열의 롱텀 forecasting을 다룬다. 이전 트랜스포머 기반의 모델은 다양한 self-attention매커니즘을 통해서 long-range 의존도를 다루었다. 하지만 롱텀에 있어서 복잡한 temproal 패턴은 모델이 의존성을 찾기 어렵게 만들었다. 또한 트랜스포머는 sparse 버전으로 pointwise self-attention을 해야 하나, bottleneck을 만든다. 따라서 AUto-formner는 Auto-correlation이라는 독창적인 분해를 통해 디자인한다. 전처리의 시계열 분해 단계를 deep model에 임베딩한다. 이는 오토포머가 복잡한 시계열의 분해능을 높일수있게 만든다. 게다가 확률이론에 따르면, auto-correlation 매커니즘을 기반으로 디자인하는것이 서브 레벨의 representation을 모으고, 의존도를 발견하게끔 한다. 이는 self-attention보다 효율 및 정확도가 높다. 특히 롱텀 forecasting 에서, Autoformer는 SOTA를 달성한다.

1 Introduction

최근 트랜스포머 기반 모델이 self-attention 매커니즘을 통해 롱텀 dependency를 포착하고 모델링 하여 성능이 좋아졌다. 하지만 예측 태스크는 롱텀 세팅에서 아주 힘든 일이다. temporal 패턴에 의해 시계열의 롱텀 의존도가 가려지고, 기존 트랜스포머는 롱텀 시계열에서 계산 복잡도가 너무 높아 시퀀스 길이의 4승에 비례한다. 이전 트랜스포머 기반의 연구들은 sparse 버전으로 self-attention을 업데이트하여 퍼포먼스가 증가하였지만, 보틀넥이 존재하였다.
복잡한 temporal 패턴에 대해서 시계열을 다루는데 있어 분해가 자주 사용되었다. 복잡한 시계열을 다루는데 사용되었으며, 예측가능한 컴포넌트들로 만든다. 하지만 시계열에서 이를 사용하기 위해서는 전처리를 수행하여만 한다. 이는 분해의 이용능력을 줄이고, 분해된 컴포넌트들의 상호작용을 간과할 수 있다. 그러므로 전처리 방법을 사용하지 않는 분해를 아키텍처를 통해 수행함으로써 깊은 예측 모델에 임베딩하고 분해 능력을 높인다. 분해는 temporal 패턴을 추출하고 시계열의 내재된 구조를 밝혀낸다. 이를 통해 시계열의 주기성을 취하는 것으로 point-wise self-attention의 구조를 대체하였다. 그러므로, 시리즈 레벨의 connection을 series 주기성의 유사도를 통해서 connection을 수행한다.
이러한 모티베이션에 따라서, AutoFormer 를 제안한다. 이는 residual encoder decoder 구조를 따르고 있지만, 분해를 위한 과정을 포함한다. 이를 innter operation을 통해서 오토포머는 롱텀 트랜드 정보와 예측된 숨겨진 변수를 분리해낸다. 이 디자인은 우리의 모델이 예측 과정에서 중간 결과를 활용함을 알 수 있다. 확률 이론에 따라, Autoformer 는 Auto-correlation 매커니즘을 활용하였고, 시계열의 주기에 따라 서브 시리즈들간의 유사도를 판별하고, 비슷한 서브 시리즈끼리 모이게 된다. 이러한 series 매커니즘은 복잡도를 낮추고, 보틀넥을 없애 효율을 높이고 SOTA 정확도를 달성한다. 본 연구의 contribution은 다음과 같다.
1. 롱텀 미래의 복잡한 temporal 패턴들을 다루기 위해서 AutoFormer를 제안하여서 깊은 예측 모델 안 아키텍처 디자인에 분해 모듈을 임베딩하였고, 이를 통해서 분해 성능을 높였다.
2. Auto-Correlation 매커니즘을 제안하여서 시리즈 레벨에 따른 정보의 취합이나 의존성 발견을 수행하였다. 우리의 매커니즘은 이전 self-attention 보다 더 진보하였으며, 동시에 계산 효율이나 정보 활용에서 유용하다.
3. AutoFormer는 기존 방법론보다 38% 더 좋은 성능을 얻었다.

2 Related Work

2.1 Models for Time Series Forecasting

ARIMA는 예측 문제를 non-stationary process를 stationary 로 바꿔 풀어낸다. Filtering 방법론 또한 예측을 수행한다. RNN또한 시계열의 temporal dependency를 모델링하는데 사용된다. DeepAR은 ar방법론으로 RNN이 미래 시계열의 분포를 모델링한다. LSTNet은 CNNS를 통해서 recurrent-skip connection을 통해서 숏텀과 롱텀의 temporal pattern을 사용한다. Attention 기반의 방법론들은 temtporal attention을 통해서 예측을 위한 long-range 의존도를 활용한다. 또한 많은 연구들이 TCN과 같이 인과관계를 모델링하려고 하였다. 최근 deep forecasting 모델은 temporal relation 을 모델링하는데 집중한다.
최근, 트랜스포머 기반의 self-attention 모델은 많은 이점이 있었다. 그러나, self-attention을 long-term 시계열에 적용하는것은 너무 계산량이 많으며 동시에 메모리와 시간을 많이 소모하게 되낟. LogTrans는 local conv를 트랜스포머에 제안하고, LogSparse attention을 수행하였다. Reformer는 local-sensitive hashing attention을 통해서 복잡도를 줄였다. 인포머는 KL-divergence를 함께 사용하여, ProbSparse attention을 하였다. 이러한 방법론들은 바닐라 트랜스포머의 self-attention 매커니즘을 개선하기 위해서 사용된 것들이지만, 아직도 이러한 방법론들은 point-wise 로 연산을 수행해야 한다는 문제점이 있다. 따라서, 본 연구에서는 Auto-correlation 매커니즘을 통해서 시계열의 내재된 주기성을 탐지하고 series-wise connection을 제공한다.

2.2 Decomposition of Time Series

시계열 분석에 기본 방법은 시계열 분해이다. 이는 시계열을 몇몇 컴포넌트들로 분해하고, 각 패턴의 카테고리를 통해서 더 예측가능하게 만든다. 시계열 예측 태스크에서는 분해가 전처리로 historical series를 미래 예측을 하기 전에 사용된다. Prophet은 trend와 seasonality decomposition와 N-BEATS를 통해 시계열 분해를 사용한다. 그러나, 이러한 전처리 방법론들은 이전 series의 분해 효과를 제한하고, 과거와 롱텀 미래의 상호작용을 무시한다. 따라서 본 연구에서는 딥 모델에 내제된 구조를 통해 시계열을 분해하고, 이는 예측 프로세스에서 지속적으로 중간 결과의 상호작용을 통해 결과를 출력한다.

3 Autoformer

시계열 예측 문제는 길이 O의 데이터를 이전 길이 I 데이터가 주어졌을 때 예측하는것으로, Input I predict O 로 표현된다. 롱텀 예측 세팅은 O가 큰 의미이고, 이전 연구의 문제점을 해결하기 위해서 분해를 예측 모델의 빌트인 모델로 임베딩하였고, AutoFormer를 제안한다.

3.1 Decomposition Architecture

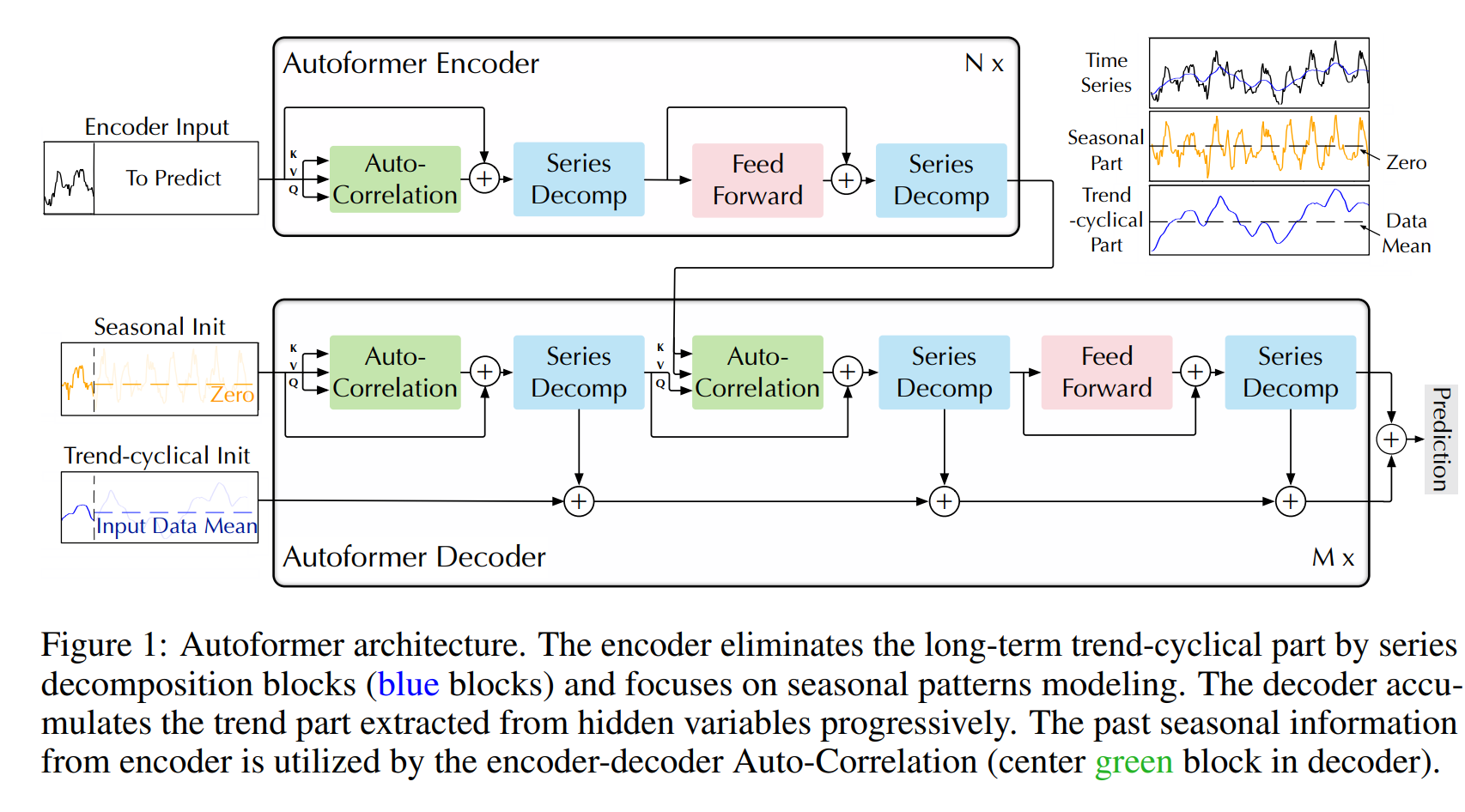
Fig.1 은 제안 방법론의 구조이다. 먼저 inner series decomposition block, Auto-Correlation mechanism, corresponding Encoder 와 Decoder 로 이루어져 있다.

Series decomposition block

시계열을 trend와 seasonal part로 분해한다. 이 2개의 파트는 각각 롱텀 progression과 sesonality를 반영한다. 미래는 알지 못하기 때문에 이를 바로 분해할수는 없다. 따라서 series decomposition block을 제안한단. 이는 AutoFormer의 내부 연산을 의미한다. 구체적으로, periodic flucuations에 대해 smooth를 하는 moving average를 취해준다. L 길이의 시계열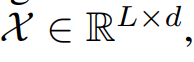 은 다음과 같으 ㄴ과정을 거쳐서 분해가 된다.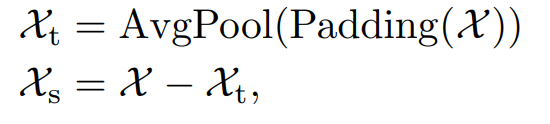
이를 다음과 같이 denote 할 수 있다.

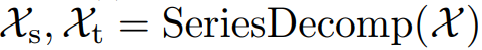
Model inputs

인코더 파트의 인풋은 이전 I 타임스텝을 의미한다.

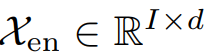
오토포머 디코더의 인풋에는 시즈널 파트와 트렌드 파트가 포함되어 있고, 이는 정제되어야 한다. 초기에는 2개의 파트로 나뉜다.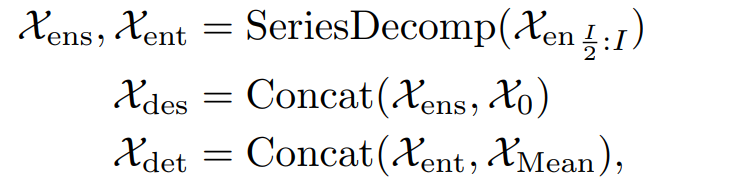
X의 ens ent는 인풋의 seasonal 과 trend 파트를 의미한다.

Encoder

Fig.1 에서 encoder는 시즈널 파트 모델링에 집중한다. 인코더의 아웃풋은 이전 시즈널 정보를 디코더가 잘 이해하도록 정제하는 과정이다. N개의 인코더 레이어가 있을 때 전체적인 l번째 인코더 레이어를 타나내는 식은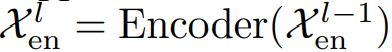
이다. 이에 대한 디테일한 인코더의 연산은 다음과 같다.

여기서 _ 는 trend 는 제거된다.

Decoder

디코더는 2개의 파트로 나뉜다. 축적 구조는 트렌드를 위한 모듈이며, stacked Auto-Correlation 매커니즘은 seasonal을 위한 것이다. 각 디코더 레이어는 inner Auto-Correlation 과 encoder-decoder Auto-Correlation 으로 나뉘는데, 각각은 예측을 정제하고, 과거의 시즈널 정보를 활용한다. 모델이 디코더에서 중간 히든 변수들을 통해 잠재 트랜드를 추출하는데, 오토포머가 지속적으로 trend prediction을 정제하고, period 기반의 의존성 정보의 개입을 제거하게 된다. M 디코더 레이어가 있다고 하면 latent variable 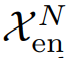이 인코더에서 나오게 되는데, l번째 디코더 레이어에 들어가는 수식은 다음과 같다.

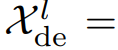
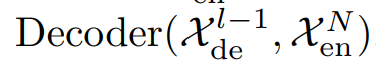
디코더의 디테일한 연산은 다음과 같다.

여기서 S, T가 의미하는건 i번째 시계열 분해 블럭을 통과한 seasonal 컴포넌와 trend 컴포넌트이다. W는 프로젝터를 의미한다.
마지막 예측은 2개의 refined된 분해 컴포넌트를 다음과 같은 식으로 합치는 것이다.

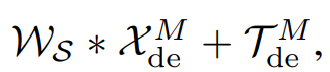
Ws는 프로젝션웨이트로, deep transformed seasonal component 를 타겟 도메인 차원으로 변형시키는 역할을 한다.

3.2 Auto-Correlation Mechanism

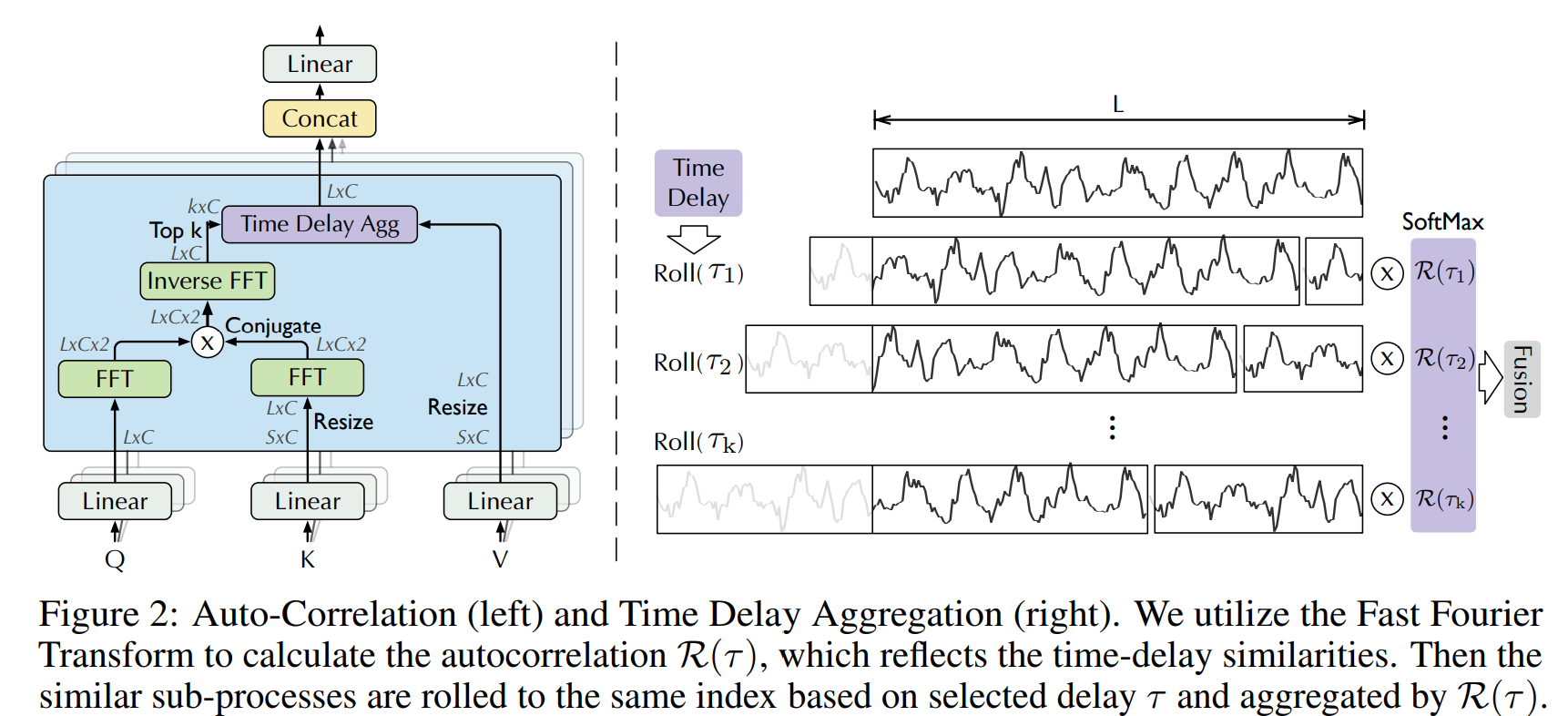
Auto-Correlation 는 주기 기반으로 의존성을 판별하는데 이는 autocorrelation을 통해 얻는다. 또한 비슷한 서브 시리즈들을 타임 딜레이 aggregation을 통해 획득한다.

Period-based dependencies

주기안의 같은 phase간에 비슷한 서브 프로세스를 보인다. 다음과 같이 이산 확률 과정에서 Autocorrelation은 다음과 같이 계산된다.

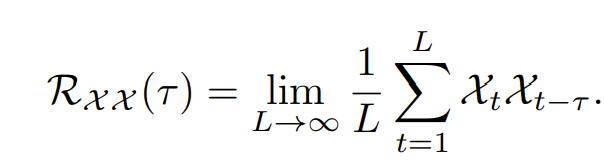
이는 시간 타우만큼 lag된 시계열과 원본 시계열간의 유사도를 비교한다. Fig 2. 에서 period length 타우에 대해서 정규화가 되지 않은 autocorrelation을 얻을 수 있다. 예측된 주기에 맞는 phase를 갖는 비슷한 서브 시리즈를 정렬할 수 있고, 마지막으로 소프트맥스 정규 신뢰도를 통해 aggregate 한다.

single head situation
길이 L의 시계열 X 이 프로젝터를 통과하면 QKV를 얻게 된다. 이를 통해 self-attention을 대체할 수 있다. Autocorrelation 매커니즘은 다음과 같이 정리된다.

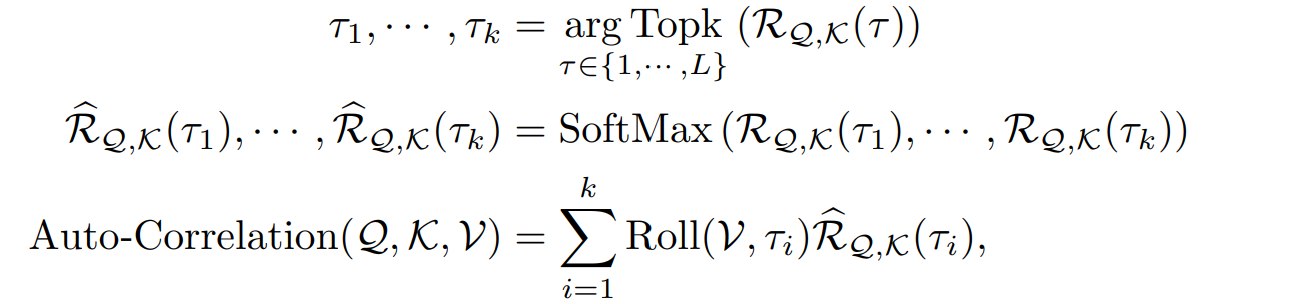
여기서 TopK 연산은 c가 하이퍼 파라미터로 다음과 같이 계산된다.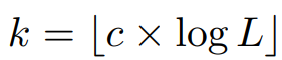
그러면 k개만큼의 쿼리와 키의 autocorrelation 이 높은 타임 딜레이 타우가 구해진다.

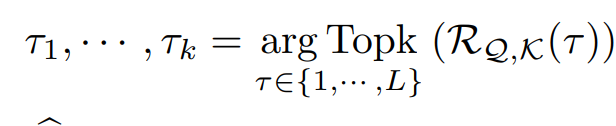
Roll(X,t) 는 타우 시간만큼의 타임딜레이를 X에 주고 shift를 하고 마지막에 붙이는걸 의미한다. 그러니 전체 시계열 길이는 동일하다.
Fig 1. 에서 K,V 는 인코더를 통해 얻어지고 O의 길이로 리사이즈되어 디코더에 들어가게 된다.

multi-head situation
여기서는 hidden variable d 채널이 존재하게 되고, h head가 있다. i번째 head의 QKV가 있게 되며 다음과 같은 연산이 헤드별로 이루어지게 된다.

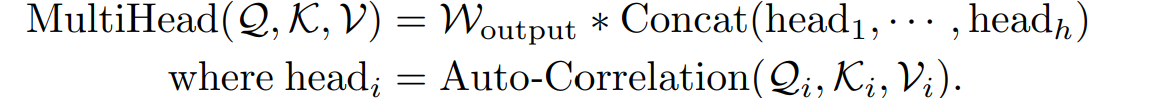
Efficient computation

주기 기반 의존성은 같은 phase의 포지션에 집중하며, 내제적으로 sparse 하다. O 시리즈를 길이 L의 시계열에 대해서 선택하게 되는데, 이전 수식의 복잡도는 O(LlogL)이다. autocorrelation 계산은 FFT로 계산되는데, 이는 다음과 같다.

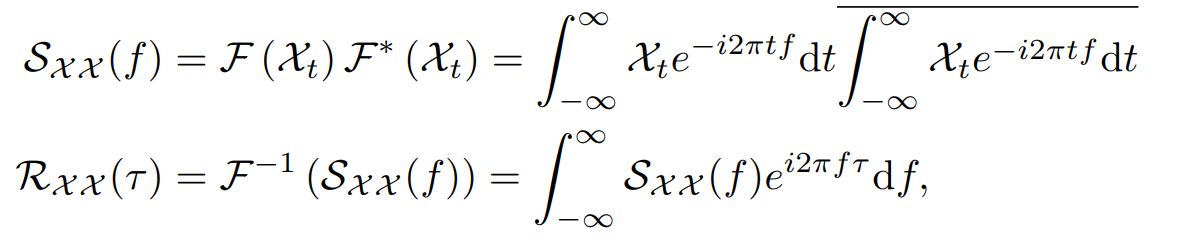
F는 FFT 연산을 의미하고, 스타는 conjugate operation으로, Sxx는 주파수 도메인 데이터를 의미한다. 시계열의 모든 lag 길이 1,2 ... L의 모든 autocorrelation은 FFT를 통해 한번에 연산이 가능하다.

Auto-Correlation vs. self-attention family

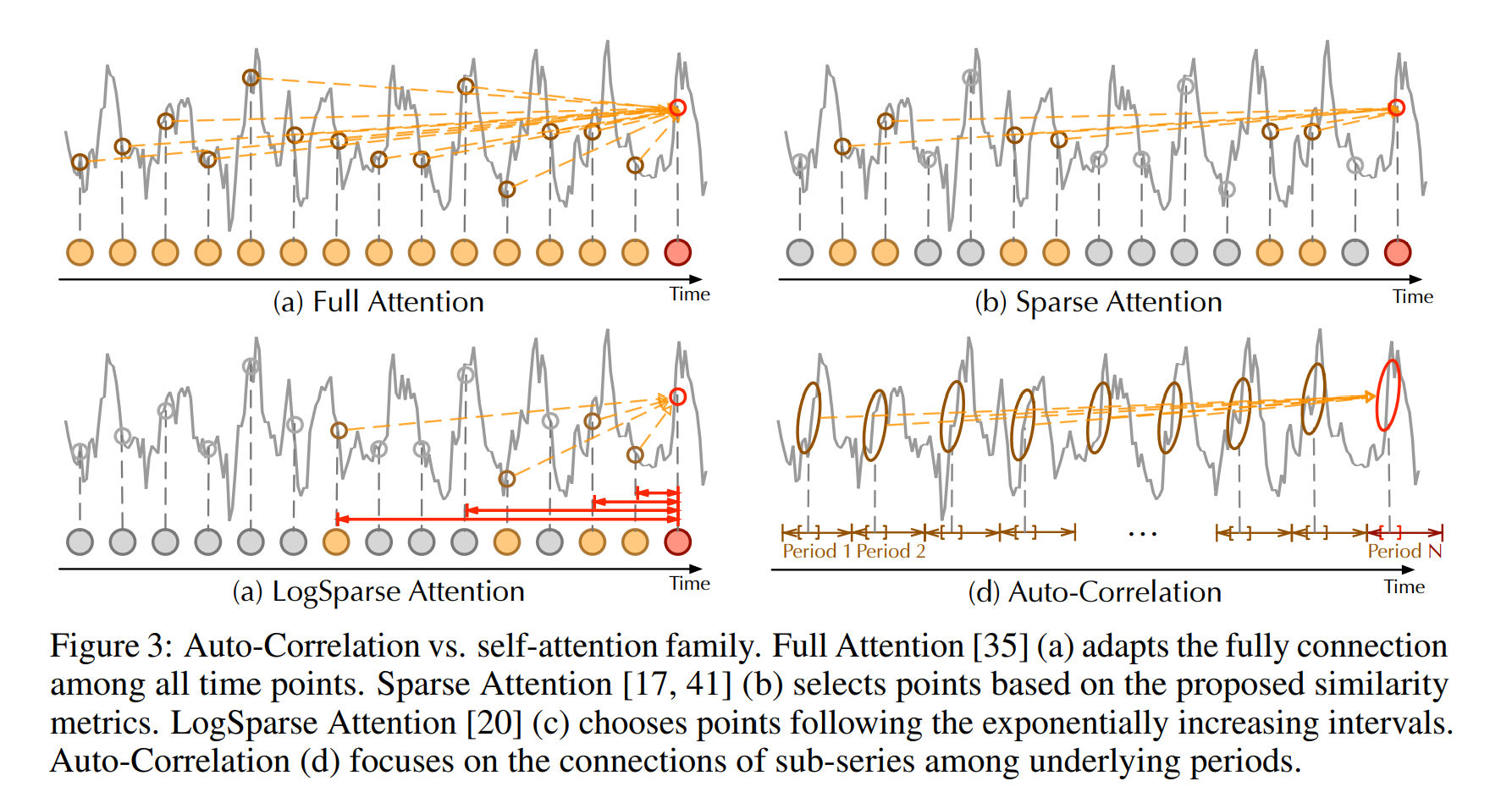
auto-coreelation은 series wise connection을 수행한다. 구체적으로 temporal 의존성을 보려고 할 떄 서브 시리즈들 간의 의존성을 주기르 기반으로 보게 된다. 대조적으로, self-attention 은 단지 분산된 포인트들끼리의 관계를 보게 된다. 몇몇 self-attention 방법론은 로컬 정보를 보기는 하지만, 단지 point wise 를 돕기 위한 정보로 활용한다. 본 연구에서는 정보 aggregation을 하기 위해서 타임딜레이 블록을 사용했고, 비슷한 서브 시리즈들을 사용한다. inherent sparsity와 서브 시리즈 레벨의 표현 aggregation을 하기 위해 Auto-correlation 은 동시에 계산 효율과 정보 사용에 효과적이다.

4 Experiments

Datasets

(1) ETT (2) Electricity (3) Exchange (4) Traffic (5) Weather (6) ILI
ETT에 대해서는 학습/테스트/검증 6:2:2 로 두었고, 다른 데이터는 7:1:2로 두었다.

Baselines

다변량 : Informer [41], Reformer [17], LogTrans [20], two RNN-based
models: LSTNet [19], LSTM [13] and CNN-based TCN [3]
단변량 : N-BEATS[23], DeepAR [28], Prophet [33] and ARMIA [1]

인풋 길이는 고정하고 예측 길이를 96, 192, 336, 720로 두고 실험을 수행

4.1 Main Results

Multivariate results

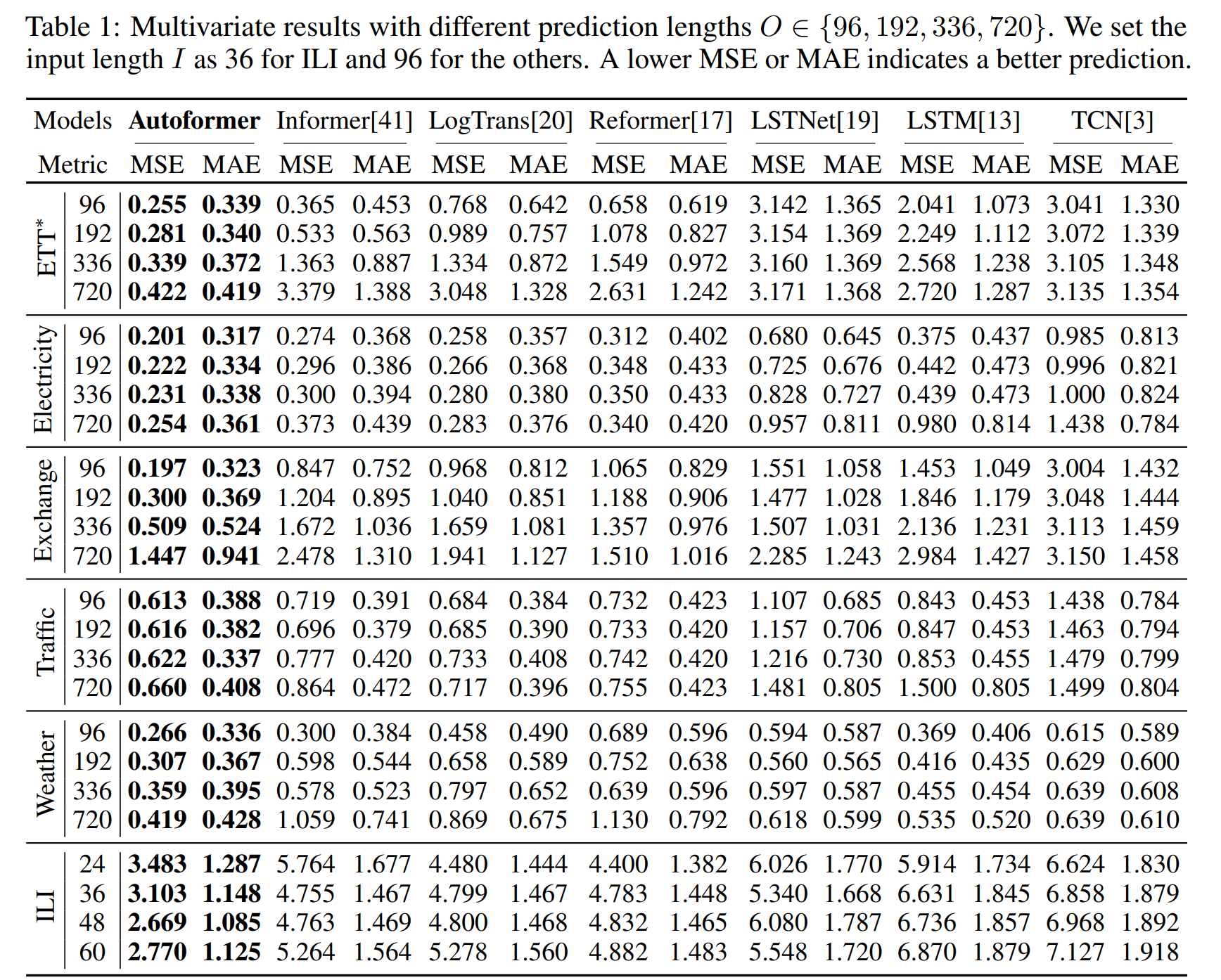
Autoformer 는 SOTA를 달성하였다. 전체적으로, 오토포머는 Exchange 데이터셋에서 특정한 주기가 없는데도 좋은 성능을 보였다. 오토포머의 퍼포먼스가 길이가 증가하더라도 일정한 것을 볼 수 있다. Autoformer가 롱텀에 더 로버스트 하다는 장점을 보인다.

Univariate results

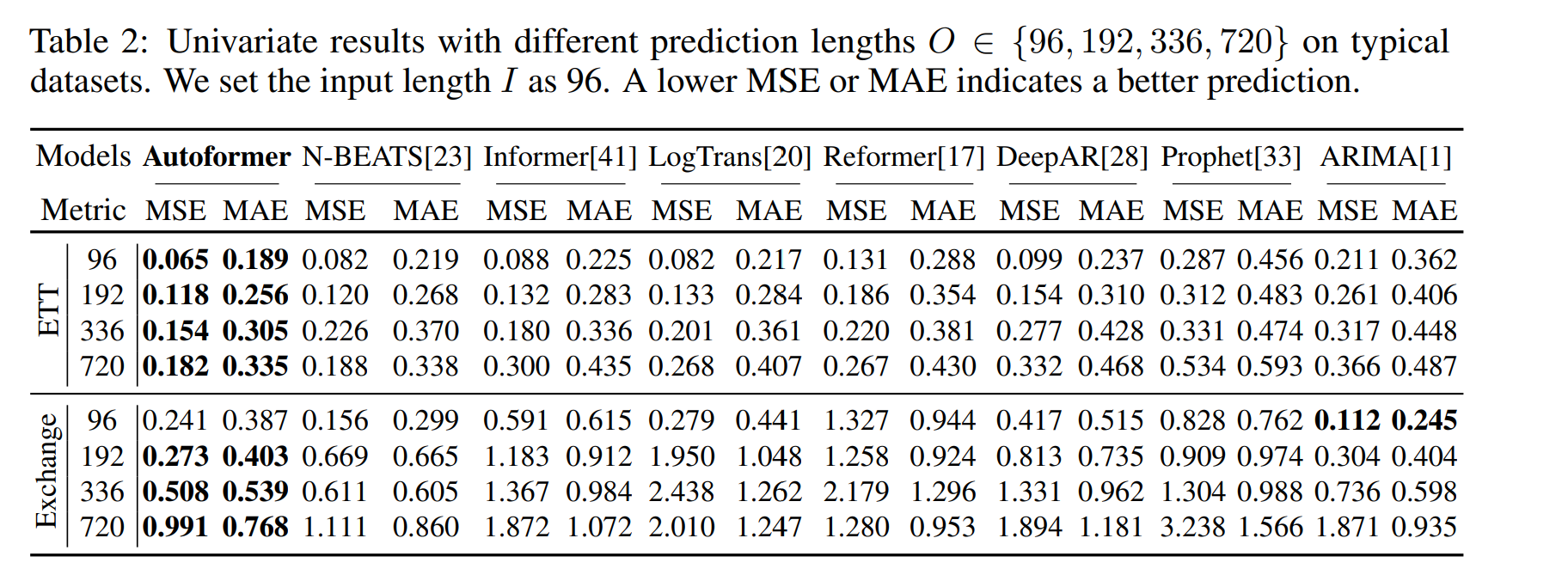
오토포머가 SOTA를 달성하였다. ARIMA가 Exchange의 96에 대해서는 성능이 좋으나, 이는 일시적인 변동에 더 잘 집중하는 알고리즘 상 성능이 조금 더 좋게 나온 것이며, 더 롱텀으로 갈 시에는 제안 방법론이 더 잘 예측하였다.

4.2 Ablation studies

Decomposition architecture

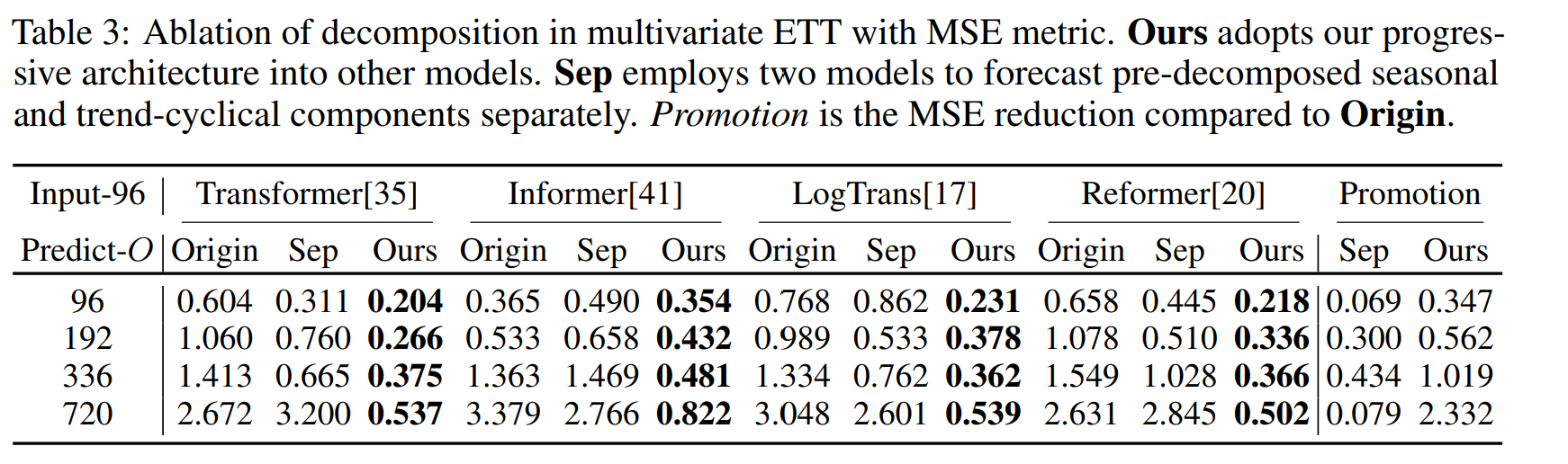
Ours는 각 모델에서 분해 모듈을 적용한 방법론이다. 다른 모델들에서 내부 구조에서 분해 모듈을 적용하였을 때 지속적인 promotion을 받을 수 있었다. 특히 O 길이가 증가할 수록 이 promotion이 증가하였다. 이를 통해 제안 방법론이 복잡한 패턴으로부터 시계열을 특징을 효과적으로 추출하고, 더 큰 모델에 쓸수록 더 좋은 성능을 보임을 알 수 있다.

Auto-Correlation vs. self-attention family

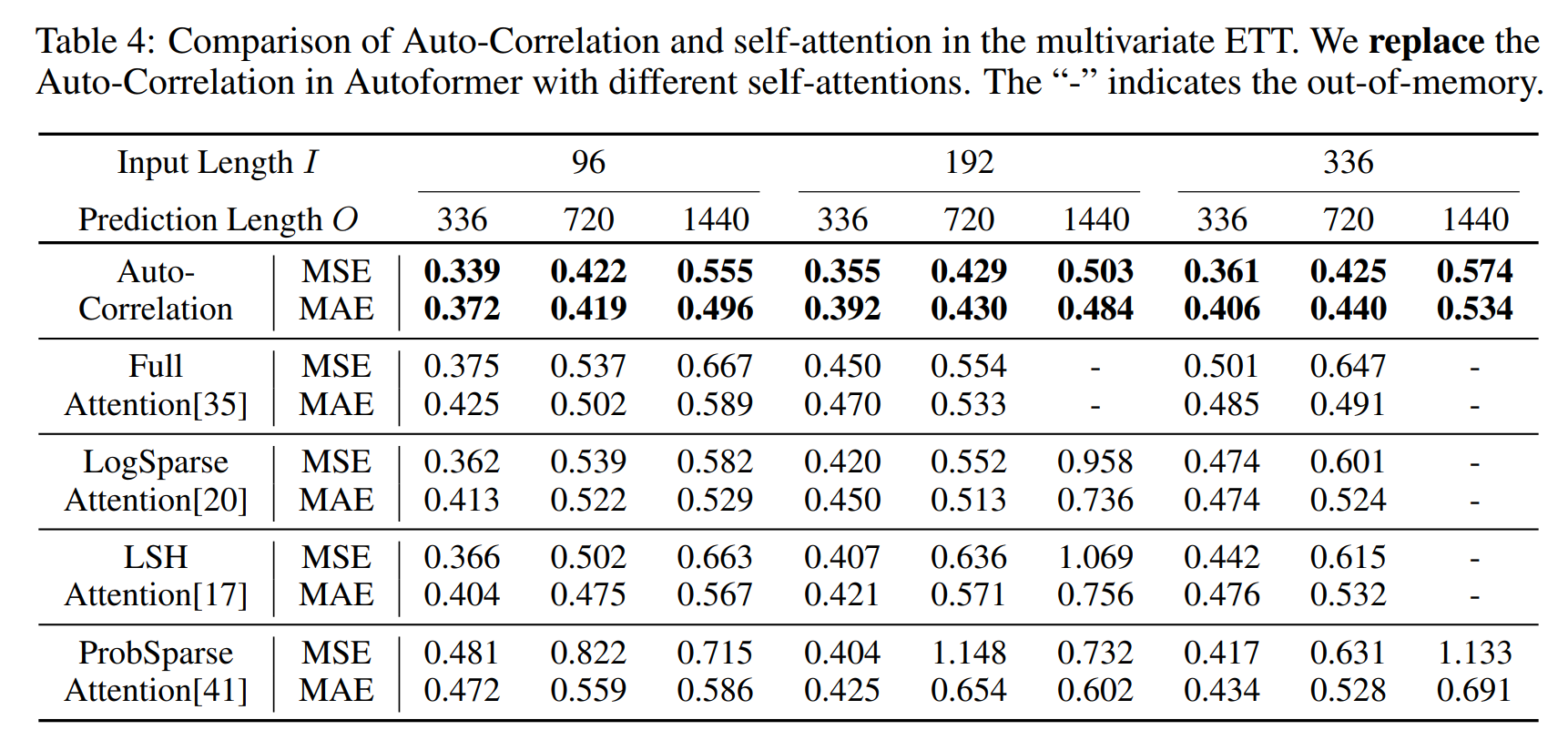
Auto-correlation이 가장 좋은 성능을 발휘하는 것을 알 수 있다. 특히 격차는 prediction lenght 가 길어질수록, 다른 것들은 아웃오브 메모리가 발생함에도 제안 방법론은 성능도 좋고 연산이 가능하였다.

4.3 Model Analysis

Time series decomposition

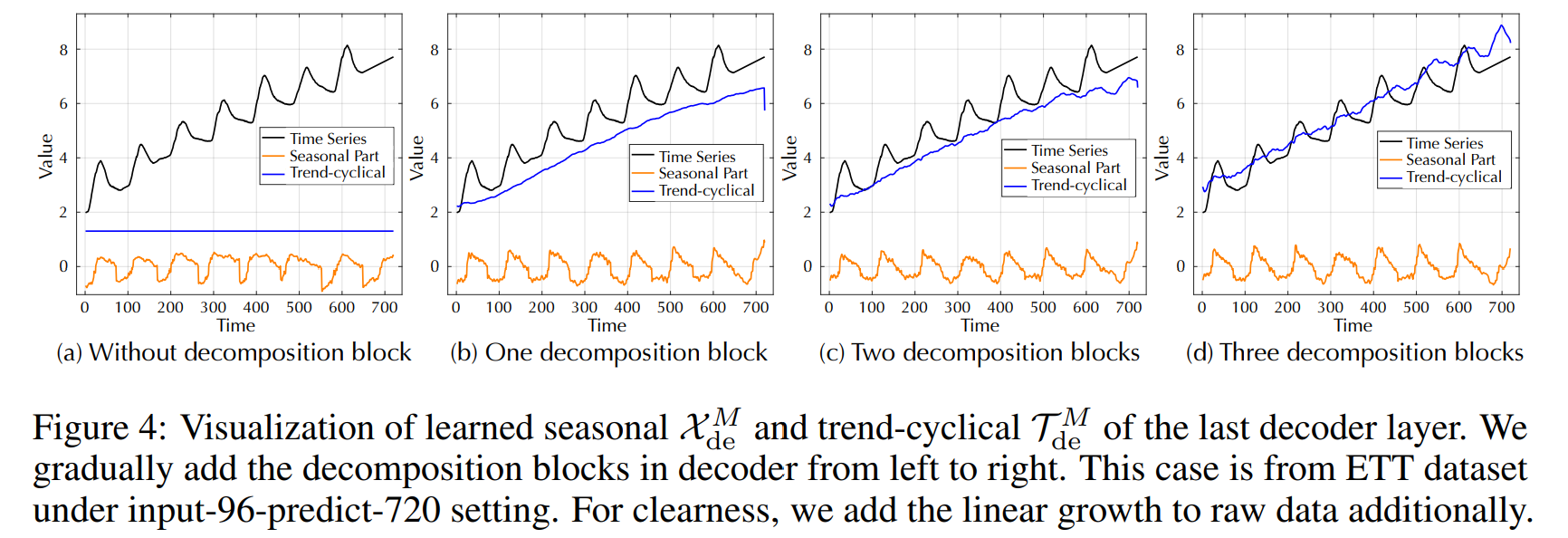
분해 블럭이 없으면 시즈널한 것을 따라가지 못한다. 또한 series decomposition 블럭을 추가함으로써 더 trend를 잘 예측하는 것을 알 수 있다. 이는 progressive한 decomposition 아키텍처를 설꼐해야하는 이유에 대해 잘 알려준다.

Dependencies learning

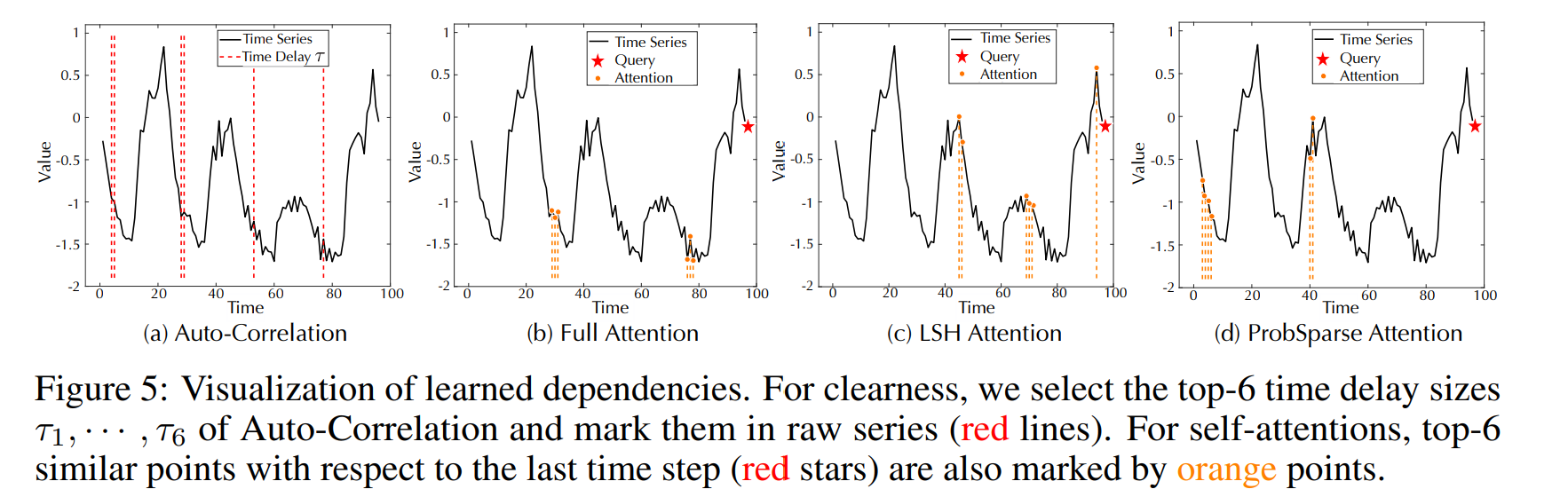
Figure 5(a) 의 타임 딜레이 사이즈는 period를 의미한다. 우리의 주기성은 서브 시리즈들을 aggregate하고, 마지막 타임 스텝에서 autocorrelation은 비슷한 서브 시리즈들을 중복이나 에러 없이 활용한다.

Complex seasonality modeling

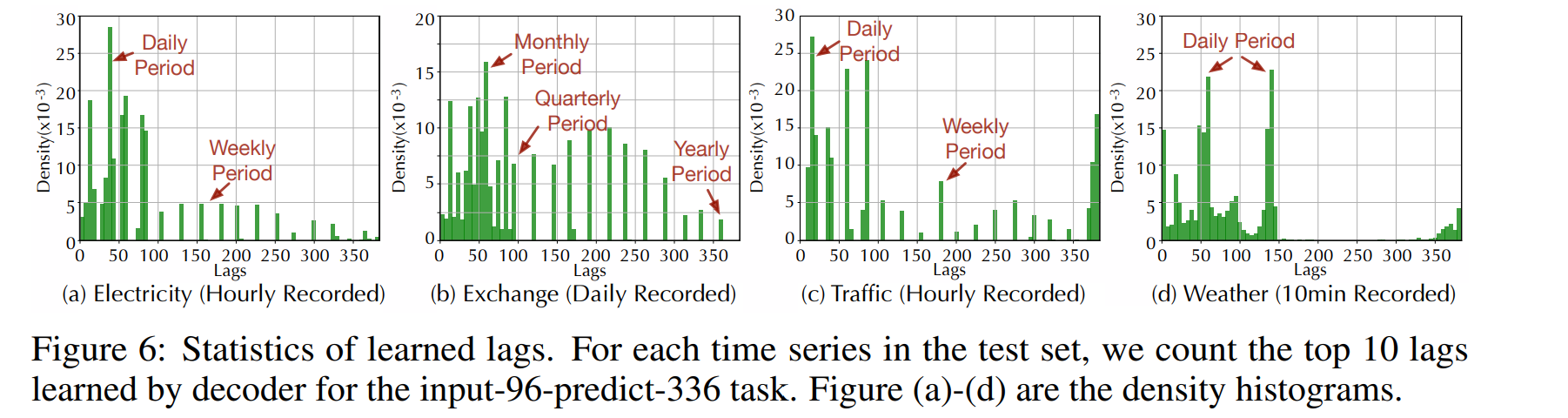
위 그림으로 Autoformer가 학습한 lags들은 실제 시즈널리티를 의미한다. Exchange 데이터의 데일리한 패턴, 한달, 분기, 년 주기의 패턴까지 포착하는 것을 알 수 있다.

Efficiency analysis

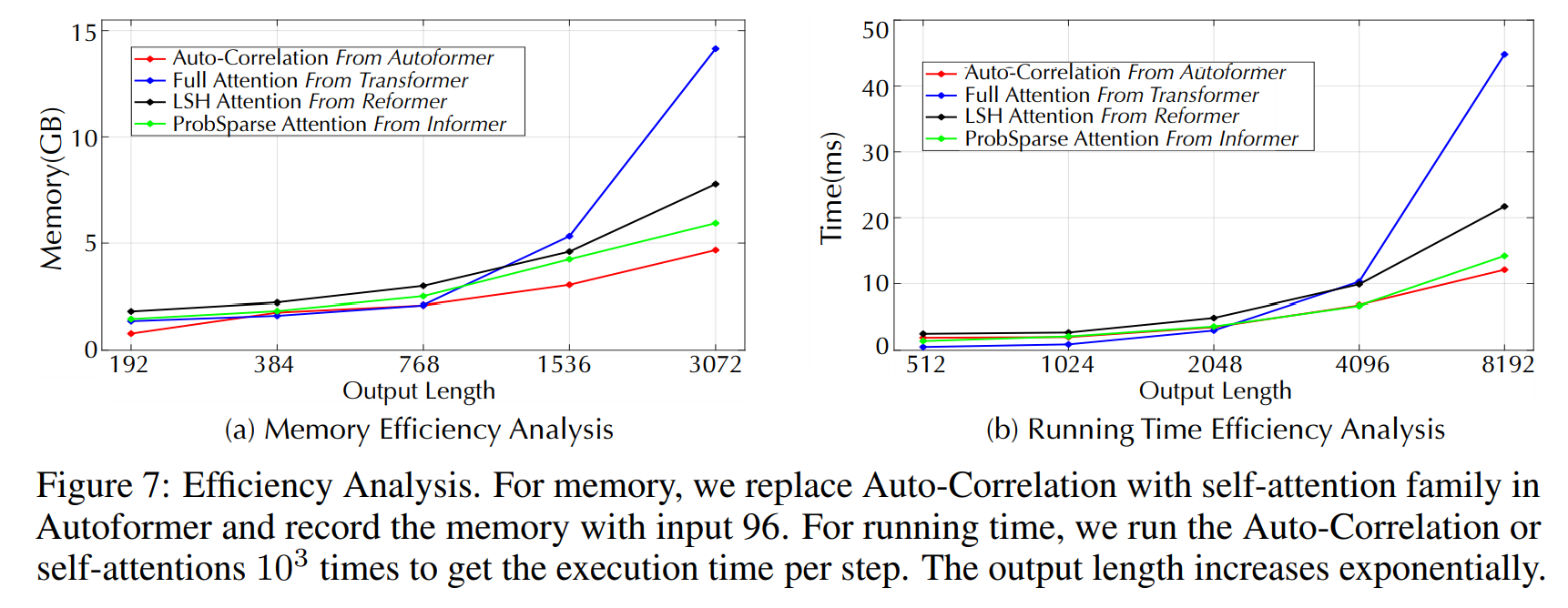
메모리와 학습시간 비교시 제안 방법론이 제일 메모리 복잡도도 낮고, 성능도 좋았다.

5 Conclusions

본 연구는 시계열을 롱텀으로 예측하는 방법에 대해서 이야기한다. 복잡한 temporal 패턴들은 모델이 예측하기 어렵게 만든다. Autoformer는 분해 아키텍처를 통해서 시계열을 임베딩하고, 예측 중간 결과를 가지고 progressive하게 서브 시계열을 모아 예측에 활용한다. 게다가 효과적인 Auto-correlation 매커니즘을 통하여 시리즈 레벨에서 비슷한 서브 시계열의 정보를 취합하여 활용한다. 오토포머는 O(LlogL) 의 계산 복잡도를 통해서 SOTA 퍼포먼스를 달성하였다.