모터 베어링의 스펙을 머신러닝 기법으로 분석하여 지도학습 기반의 이상치 탐지를 하는 것이 기존의 연구 방향이었음. 이 논문에서는 데이터 분석 기법을 통해 normal condition에서의 bearing failure을 분석함. 모터 전류 센서 신호에서 power spectrum을 만들고 bins로 그룹핑하여 GMM 모델을 적용하여 motor의 normal condition을 학습함. 그리고 likelihood 함수를 이용하여 이상치를 탐지함. 제시된 방법으로 insufficient grease 상황에서의 베어링 컨디션의 이상치를 구분하는 성능 향상됨
이전에는 frequency analysis 방법(푸리에 변환, 이상 웨이블렛 변환, 웨이블렛 변환) 다른 frequency 대역에서 다른 시그널들을 분리히해내 분석해냄
이전 리서치들은 failures의 원인을 베어링 스펙과frequency와의 상관관계를 찾아 분석을 했지만, 이것은 inner raceway 혹은 outer raceway 크랙에 영향을 받음.
이전 연구는 2가지 문제점이 있음.
1. bearing failure를 감지하기 위해서 베어링 스펙이 필요
2. supervised learning 방법이었음
-> 이 논문에서는 모터 베어링 failures를 라벨링 되어 있지 않은 normal 데이터로부터 노말 컨디션 패턴을 power spectrum sensor signal로부터 생성해냄
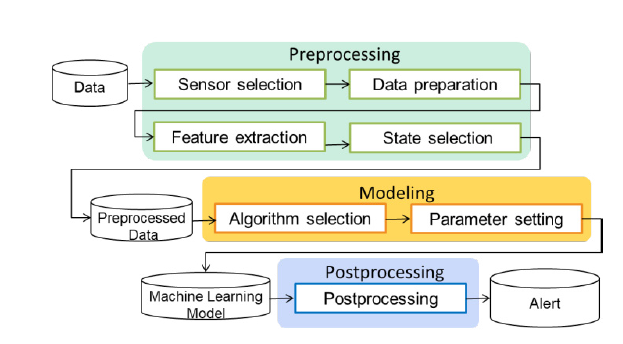
data analytics process를 다음과 같이 진행함
Preprocessing : sensor data를 modeling 의 input 데이터로 변환
센서의 시계열 데이터를 power spectrum 데이터로 변환
파워 스펙트럼을 통해 모터 driving frequency와 베어링 파손으로 인한 frequency를 구분할 수 있음.
state selection 단계에서는 stable condition을 motor driving frequency를 통해 골라냄
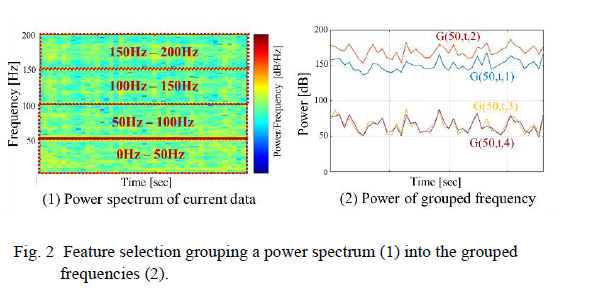
Feature Extraction 단계에서는 파워 스펙트럼을 bin으로 그룹핑하여 input data의 수를 줄이고, small observation errors를 줄임
ex) power spectrum의 0-200Hz를 4 bins로 equal frequency range 50Hz로 나눔
P(t,f)는 frequency f , time t에서의 power를 나타냄. funit은 frequency의 bin width를 의미함(50Hz)
따라서 유닛 구간의 Power spectrum을 적분한 것이 G(funit,t,i) 가 됨
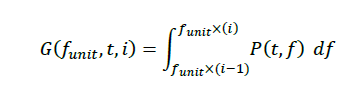
파워 스펙트럼 : 시간적으로 변동하는 어떠한 파형이 있을 때, 주파수 성분이 어떠한 크기로 포함되고 있는가를 나타냄
가로 축은 f를 나타내며,
random process 모형을 주파수 영역으로 변환하는 것으로, 푸리에 변환과 달리 시계열의 위상 정보는 스펙트럼에 나타나지 않음
스펙트럼 추정 시에는 시계열 구간을 짧게 나누고 각 구간에 윈도우를 씌운 뒤 FFT 계산을 통해 나온 값을 평균함
-> 시계열 자료의 주기와 크기에 대한 분석을 수행하며 주기함수들의 영향력을 주파수에 대한 밀도함수로 나타냄으로써 가장 탁월한 주기를 찾아내는 방법임.
Modeling : 머신러닝 알고리즘을 정하고 파라미터 세팅작업
Postprocessing : condition monitoring system에서 필요한 정보를 생성하는 단계
PCA, 클러스터링, SVM 방법 순으로 진행
클러스터링에 GMM을 사용했는데, unsupervised에서 well-known이며 normal condition에서도 복잡한 분포 특성을 가지는 power spectrum을 잘 represent 하기 때문
GMM 파라미터는 iterative Expectation maximization 알고리즘을 통해 노말 컨디션의 데이터 트레이닝을 통해 estimated 됨
GMM parameters (𝜇, Σ, 𝜋) 를 계산하는데, mean 𝜇, covariance Σ, mixing coefficient π임.
초기값을 통해 learning data가 각 cluster에 속할 확률을 구하고, log likelihood 함수가 maximum value가 될 때까지 반복함
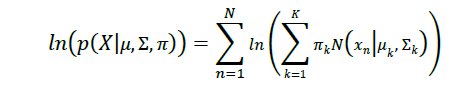
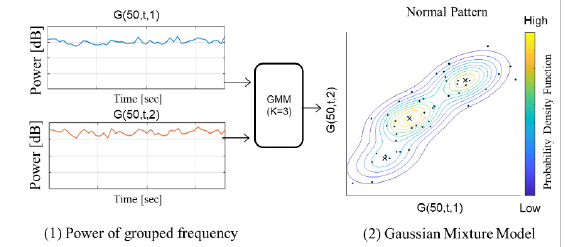
optimal한 가우시안 분포 수인 K와 optimal한 bin width를 정하기 위해 Bayesian Information Criterion 을 K와 funit에 대해 설정. 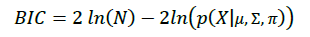
Postprocessing
포스트 프로세싱은 모니터링 시스템에서 observed data X를 받았을 때 베어링 컨디션을 GMM 파라미터를 통해 정량화함.
𝑙n(𝑝(𝑋(𝑜berved)|𝜇, Σ, 𝜋)) 를 정해진 Threshold 와 비교함. 이는 Safety Integrity Level (SIL)과 결합되어 만들어지는데, SIL 레벨은 타겟을 1, 2, 3, 4로 나누어져 SIL 레벨이 높을수록 민감함.
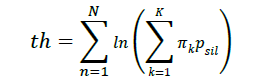
Psil 은 10^(-5) 등으로 정해진 값
Experiment
테스트 베드 구성
normal bearing을 fixed load, 50Hz 구동 상황. 그리스가 부족한 상황을 fault mode로 정함. 이 베어링을 아세톤 워싱을 하여 2일 동안 운전시킴.
전류 센서를 선택했는데, 이 이유는 current sensor가 부착되어 있다면 더 유용한 분석이 가능함.
샘플링 주파수는 5000Hz이며 시계열 데이터를 power spectrum data로 변환함.
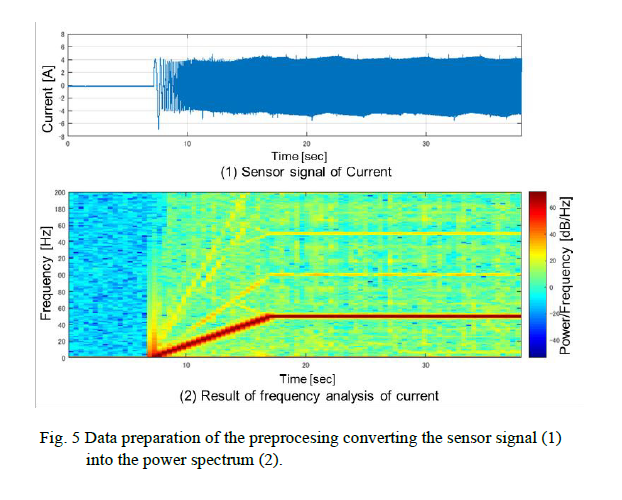
기동을 시작하고 나서 17초가 지난 뒤 전류 신호의 파형이 50Hz를 따라감을 알 수 있음
stable condition을 motor driving frequency가 50Hz인 상황으로 추출함
feature extracion은 bin의 두께는 1Hz 부터 2000Hz까지 설정하여 파워를 그룹함
모델링에서는 노말 데이터에 대한 K값에 대해 GMM 파라미터를 estimate하고, optimal number of K&bin 두께를 결정함
postprocessing에서는 replaced된 베어링의 likelihood를 계산하여 쓰레쉬홀드를 결정.
실험 결과
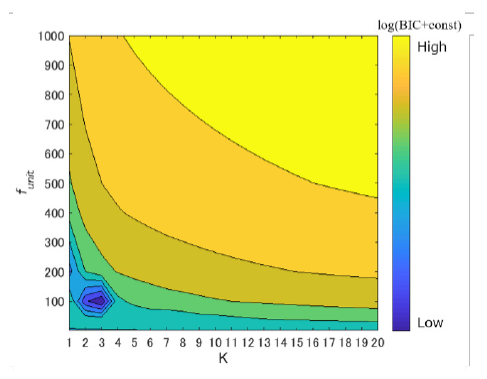
노말 컨디션을 3분동안 학습하여 BIC의 최저 값을 찾은 결과, 100Hz와 가우시안 분포 갯수 3개가 가장 이상적이었음
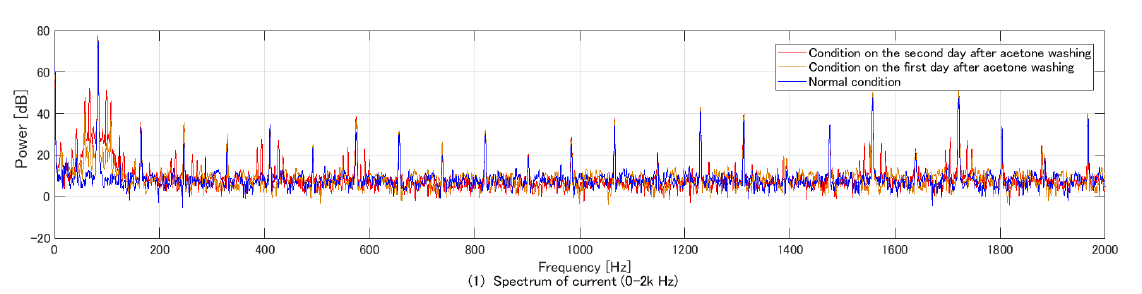
이 결과는 베어링 그리스를 없앤 후 1일차와 2일차의 파워 스펙트럼을 0~2000Hz 에 대해 나타낸 것임
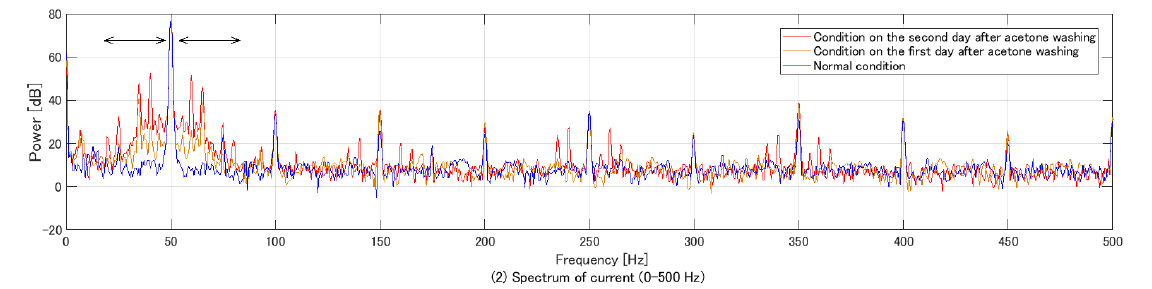
이 결과는 동일하지만, 500Hz까지만 비교한 것.
Current 시그널이 동작 주파수 50Hz에서 작동하기 때문에 피크가 50Hz 주변에서 나타남을 알 수 있음.
파란색인 노말 컨디션에서는 50Hz에서만 작동했지만, 이 분포에 이상이 생김을 알 수 있음.
이 이유가 모터의 회전이 hindered 되어서 생겼다고 볼 수 있음
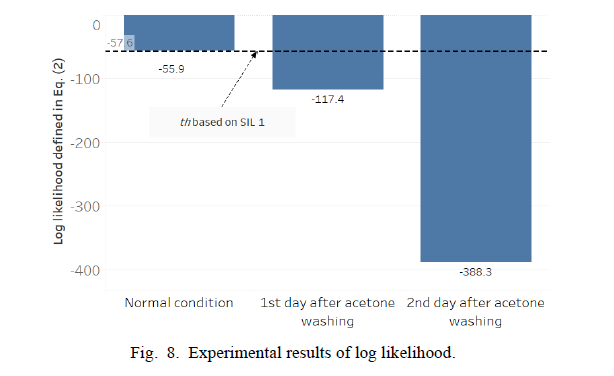
노말 컨디션, 1일차, 2일차의 average likelihood 를 계산한 결과 쓰레쉬홀드는 10^-5의 SIL 1을 기반으로 계산됨
Discussion
Area Under Curve (AUC) 를 활용하여 검증 진행
제시된 방법과 conventional method(베어링 스펙을 통한 이상검출)를 비교
베어링 스펙에 의해 fc(볼베어링 cage failure과 관련된 진동 주파수)가 주어지며, 이것을 구동 주파수에서 정수배만큼 더하거나 빼서 이상치를 검출하였음
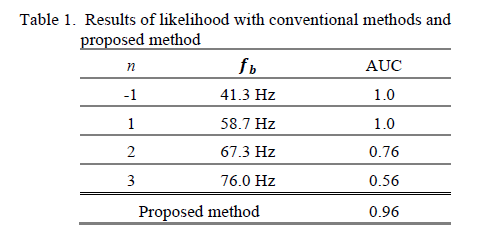
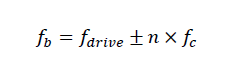
베어링 스펙이 주어진 상태에서 AUC는 1.0을 나타냈었음. 하지만 베어링의 스펙이 없는 상태에서도 비슷한 결과물을 나타냄.
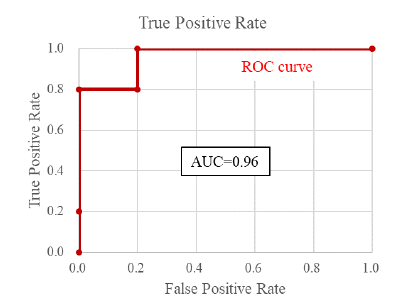
Conclusion
motor-bearing failure를 검출하는데 unsupervised learning 이 활용되어 no abnormal data에서도 충분히 활용가능함을 보임
미래 research에서는, 잔존수명 예측 진행할 예정.