Abstract
high-dimentional time series data에서는 inter-sensor relationship을 capture하는 것이 필요함. 기존의 모델은 explicity하게 relationship을 learn 하지 않았지만, 우리의 approach는 structure learning approach를 graph neural network 및 attention weight을 활용하여 anomalies 를 detect함
검증을 통해 baseline approach보다 더 효과적으로 anomalies를 detect하고, sensor들 간의 correaltion을 capture하며, root cause를 알수 있게 해줌
Introduction
sensor data의 complexity가 늘어남에 따라 data를 모니터링하는데 어려움이 생김. 고차원의 data의 anomalies를 operator에게 explainable하게 빠르게 전달해야 함
labeled anomalies 가 거의 없으므로, unsupervised로 문제를 해결해왔음. linear model-based approaches, distance-based methods, one-class methods based on support vector machines등이 있는데 이들은 상대적으로 센서들간의 inter-relationship을 간단하게 모델링했음
최근, Autoencoders Generative Adversarial Networks, LSTM-based approaches 등이 유행했지만 explicitly learn 하지 않는다는 단점이 있어 inter-relationship을 알기 힘듦
이를 해결하기 위해 graph neural networks 가 적합
graph-structured data에 좋음
graph convolution networks 및 graph attention networks를 포함하여 multi-relational approaches임
이를 anomaly detection에 적용하기 위해서는 2가지의 main challenge가 있음
1. different sensors have very different behaviors가 있음. 하지만 GNN은 각 노드의 모델 파라미터를 같은 것을 사용함.
2. the graph edges (i.e. relationships between sensors) 는 초기에 알지 못함.
따라서, novel Graph Deviation Network를 제시함
이는 learns a graph of relationships between sensors, 패턴으로부터 detects deviations 함.
4개의 main component가 있음
1. Sensor Embedding
2. Graph Structure Learning
3. Graph Attention-Based Forecasting
4. Graph Deviation Scoring
이 연구의 Contribution
1. We propose GDN
2. 수처리 플랜트의 dataset으로 GDN이 baseline approach보다 성능이 좋음을 보임
3. Case Study를 통해 GDN provides an explainable model임을 보임
Related Work
Anomaly Detection
classical method
density-based approaches (Breunig et al. 2000)
linear-model based approaches (Shyu et al.2003)
distance-based methods (Angiulli and Pizzuti 2002)
classification models (Sch¨olkopf et al. 2001)
detector ensembles (Lazarevic and Kumar 2005)
Recent method
autoencoders (AE) (Aggarwal 2015)
variational autoencoders (VAEs) (Kingma and Welling 2013)
autoencoders combining with Gaussian mixture modelling (Zong et al. 2018)
Multivariate Time Series Modelling
model the behavior of a multivariate time series
based on its past behavior (Bl´azquez-Garc´ıa et al. 2020)
Classical methods
auto-regressive models (Hautamaki, Karkkainen, and Franti 2004)
auto-regressive integrated moving average (ARIMA) models (Zhang et al.2012; Zhou et al. 2018)
deep learningbased time series methods
Convolutional Neural Network (CNN) based models (Munir et al. 2018)
Long Short Term Memory (LSTM) (Filonov, Lavrentyev, and Vorontsov 2016; Hundman et al. 2018a; Park, Hoshi, and Kemp 2018)
Generative Adversarial Networks (GAN) models (Zhou et al. 2019; Li et al. 2019)
Graph-based methods
probabilistic
graphical models, which encode joint probability distributions (Bach and Jordan 2004; Tank, Foti, and Fox 2015)
-> staionary time series에 디자인 되어 있어 complex하고, non-stationary time series에 대해서는 어려움이 있음
Graph Neural Networks
GNNs가 Complex pattern modelling을 successful한 approaches였음
GNNs는 state of a node 가 이웃 node의 state에 영향을 받는다고 가정함
Graph Convolution Networks (GCNs) (Kipf andWelling 2016)
graph attention networks (GATs) (Veliˇckovi´c et al. 2017)
GNN-based
models can perform well in traffic prediction tasks (Yu, Yin,
and Zhu 2017; Chen et al. 2019)
Applications in recommendation systems (Lim et al. 2020; Schlichtkrull et al. 2018)
relative applications (Wang et al. 2020)
GNN 이 large-scale multi-relational data를 model하는데 효과적임을 나타냄
하지만, 이 방법론은 다른 행동을 하는 각 node들에 같은 parameter를 사용했다는 단점이 있음
따라서, very different behaviors of different sensors에 대해 대응이 부족함
또한, GNNs 은 보통 graph structure를 인풋으로 요구하는데, 보통은 the graph structure is initially unknown 하므로 data로부터 학습해야 함
3. Proposed Framework
3.1 Problem Statement
N센서로부터 Ttrain 시간 동안 학습
training data 는 노말 데이터로 구성된다고 가정
Ttest는 binary label로 a(t) = {0,1} 로 1이면 anomaly 값을 가짐
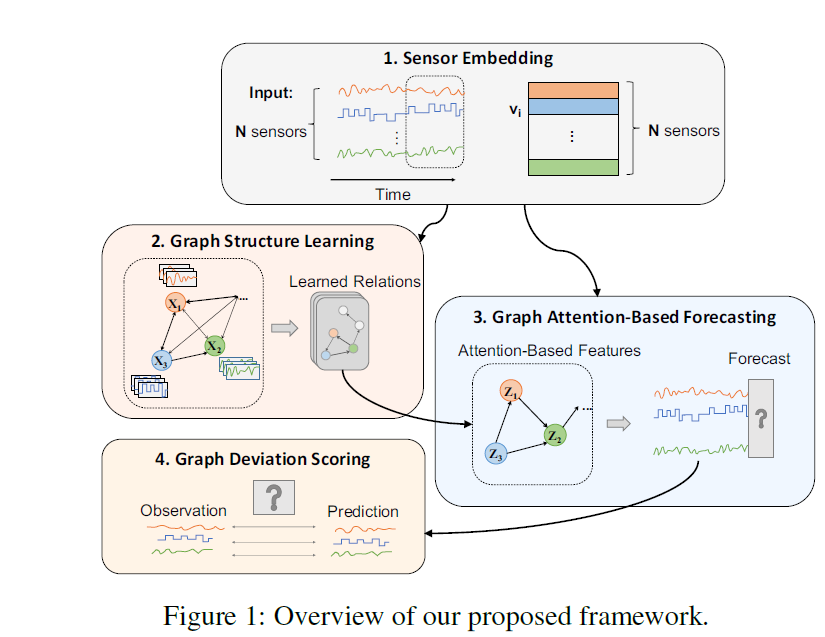
3.2 Overview
- Sensor Embedding : 임베딩 벡터를 사용하여 각 sensor의 unique characteristics를 캡쳐함
- Graph Structure Learning : 센서 사이의 dependence relationship을 캡쳐함
- Graph Attention-Based Forecasting : 각 센서의 future value를 forecast하는데, neighbor로부터의 graph attention으로부터 예측
- Graph Deviation Scoring : learned relationship으로부터 deviation을 identifies하고, loacalize 및 explains 함
3.3 Sensor Embedding
embedding vector를 통해 각 characteristics를 represent
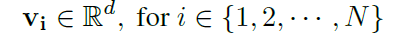
embedding은 randomly 하게 initialized 되며 학습이 진행됨
Vi 가 비슷할수록 비슷하게 행동한다는 의미이므로, related 되었다고 볼 수 있음. embedding은 다음과 같이 2가지로 사용됨
1) structer learning : 어떤 센서가 다른 센서와 related 되었는지
2) attention mechanism : attention을 이웃을 통해 heterogeneous effects를 다른 타입의 센서로부터 perform함
3.4 Graph Structure Learning
directed graph를 사용하여 노드는 각 센서를 represent, edge는 dependency relationship을 represent 함
directed graph 를 사용하는데, 센서간의 dependency 패턴이 대칭일 필요가 없기 때문임.
adjacency matrix A를 사용하여 directed graph 표현
Aij represents the presence of a directed edge from
node i to node j
이 연구의 framework는 flexible한데, 2가지 케이스에 적용 가능
1. usual case로 prior information 가 없는 경우
2. prior information이 있는 경우
Prior information은 candidate relations으로 나타남
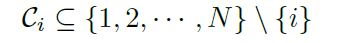
Prior information이 없는 경우 i의 dependency를 구하기 위해 embedding vector에서 simimarity를 구함
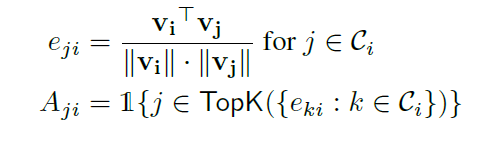
normalized dot product와 candidate relation을 구함
normalized dot product에서 Top K를 정한 다음, graph attention-based model을 define함
3.5 Graph Attention-Based Forecasting
forecasting-based approach, at time t, sliding window of size w를 통해 모델 인풋
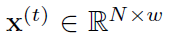
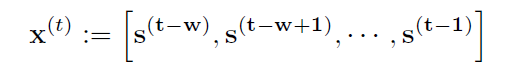
Feature Extracter
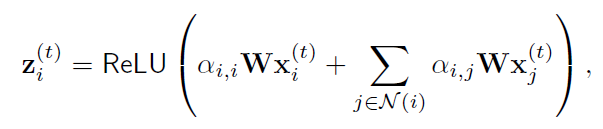
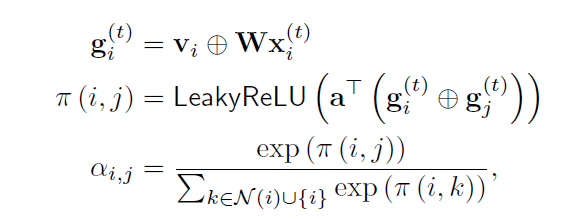
특징 추출부는 센서 임베딩 벡터를 다른 타입의 센서의 다른 행동들을 characterize화 함
Output Layer
위의 Feature extractor에서 나온 N 노드 각 zi가 나옴
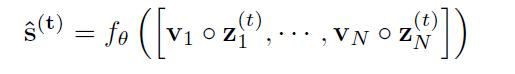
모델의 Predicted output은 St로 나타남
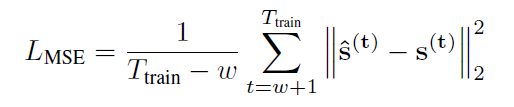
이를 실제 obervation값과 비교하여 loss function을 만듦
3.6 Graph Deviation Scoring
본 모델은 computes individual anomalousness scores for each sensor,combines them into a single anomalousness score for each time tick 함
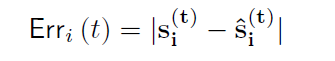
Error value 를 time t에서 sensor i의 계산
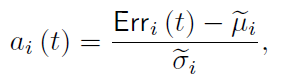
deviation values normallization을 진행
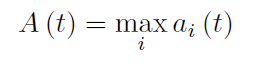
전체 값중에 max를 취함
급작스런 change를 dampen하기 위해 simple moving average(SMA)를 사용
smoothed scores As (t) 를 얻음
마지막으로, time tick t 가 anomaly라고 라벨되고, As(t) 가 fixed threshold를 넘어선다고 하면 이상치로 탐지함
threshold는 검증 데이터셋을 통해 max of As(t)로 사용함
4. Experiments
RQ1 (Accuracy)
RQ2 (Ablation)
RQ3 (Interpretability of Model)
RQ4 (Localizing Anomalies)
실험을 통해 4가지를 봄
4.1 Datasets
SWaT(Secure Water Treatment)
WADI(Water Distribution)
Training set의 2주간의 normal 데이터를 학습 데이터로 사용함
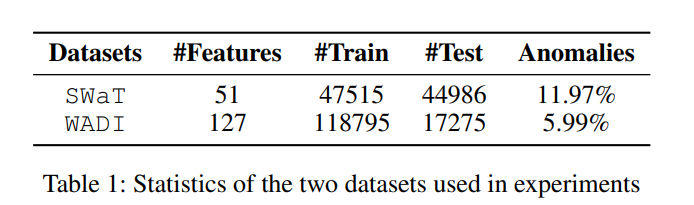
시스템이 가동되고 안정되기까지의 시간을 고려하여 eliminate the first 2160 samples 함
resulting label 은 10초 동안에 가장 많은 빈도수를 나타낸 라벨임
4.2 Baselines
PCA: Principal Component Analysis (Shyu et al. 2003)
KNN: K Nearest Neighbors
FB: A Feature Bagging detector
AE: Autoencoders
DAGMM: Deep Autoencoding Gaussian Model joints deep Autoencoders and Gaussian Mixture Model
LSTM-VAE: LSTM-VAE (Park, Hoshi, and Kemp 2018) replaces the feed-forward network in a VAE with LSTM to combine LSTM and VAE
MAD-GAN: the LSTM-RNN discriminator along with a reconstruction-based approach (Li et al. 2019)
4.4 Experimental Setup
환경
Pytorch (Paszke et al. 2017) version 1.5.1 with CUDA 10.2 and PyTorch Geometric Library (Fey and Lenssen 2019) version 1.5.0
학습 디바이스
Intel(R) Xeon(R) CPU E5-2690 v4 @ 2.60GHz and 4 NVIDIA RTX 2080Ti graphics cards
학습 파라미터
Adam optimizer, learning rate 1 × 10−3, (β1, β2) = (0.9, 0.99), 50 epochs, early stopping(patience of 10), embedding vectors with length of 128(64), k with 30(15), hidden layers of 128(64) neurons for the WADI (SWaT) dataset, sliding window size w as 5
4.5 RQ1. Accuracy
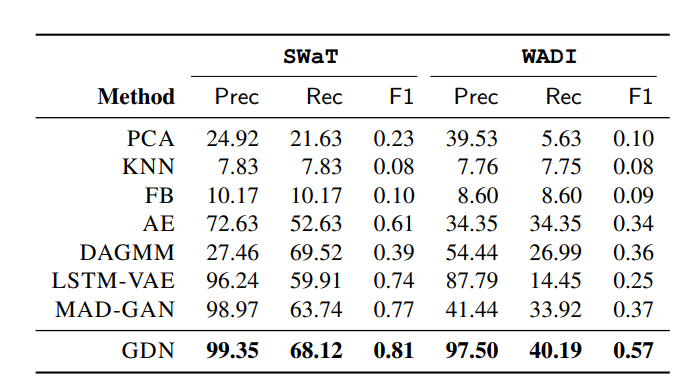
GDN 방법이 더 좋은 성능을 보임
-> unbalanced and high-dimensional attack scenarios 에서 효과적
4.6 RQ2. Ablation
모델 퍼포먼스 degrade를 component를 하나씩 제외하면서 측정
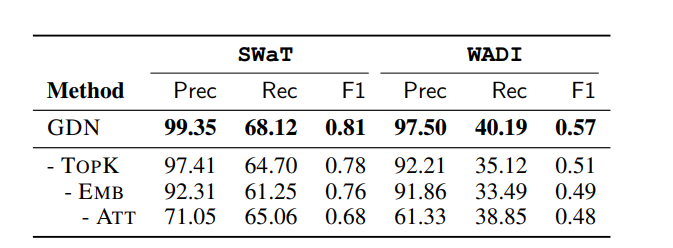
1. Replacing the learned graph structure with a complete graph
퍼포먼스가 낮아짐을 확인할 수 있음, WADI와 같이 large-scale dataset에서 특히 중요함을 알 수 있음
2. removes the sensor embedding from the attention mechanism
성능이 낮아짐을 볼 수 있고, 따라서 embedding feature가 learning weight coeffient를 잘 학습함을 알 수 있음
3. Removing the attention mechanism
가장 큰 차이로, 센서는 다른 동작을 보이기 때문에 모든 이웃을 동등하게 취급하면 성능이 매우 낮아짐을 알 수 있음
learned graph structure, sensor embedding, and attention mechanisms 셋 다 잘 작동함을 알 수 있음
4.7 RQ3. Interpretability of Model
Interpretability via Sensor Embeddings
sensor embedding vectors를 t-SNE(Maaten and Hinton 2008) 사용
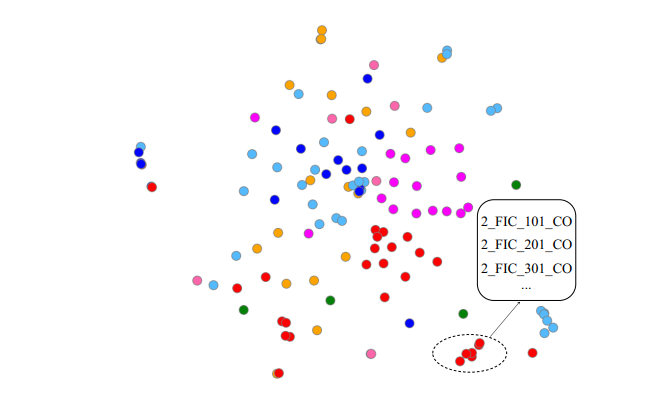
WADI에 대해서 t-SNE를 사용
Node color는 class를 의미하고, circle은 2 FIC x01 CO 센서의 loaclized clustering을 의미함
따라서 localizing을 통해 비슷하게 행동하는 센서들을 묶을 수 있음
이것을 검증하기 위해 WADI 시스템에서 7 class를 color함
Projected 2D SPACE에서 circle된 sensor들은 실제 WADI water system에서 비슷한 역할을 하는 것으로 확인됨
Interpretability via Graph Edges and Attention Weights
Edges 는 다른 센서와 어떻게 연관되어 있는지를 보여주는 것임. 게다가, attention weight은 각 노드의 이웃이 동작에 얼마나 중요한지를 알려줌
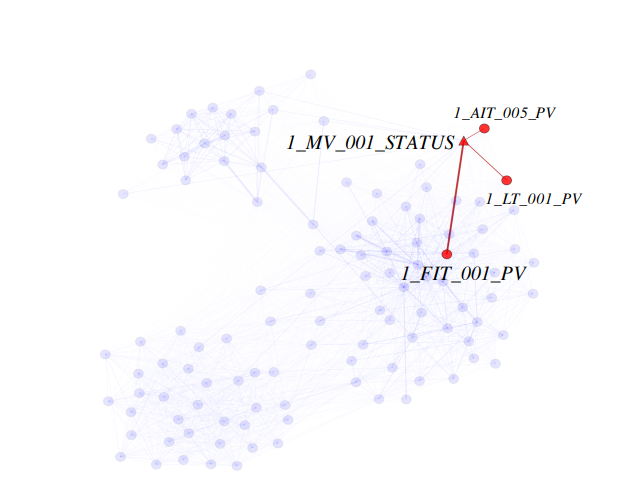
WADI datgaset의 learned graph의 예시로 이는 case study에서 자세히 분석할 예정
4.8 RQ4. Localizing Anomalies
learned graph로 edge들이 weighted by their attention weights 임을 알 수 있음.
알려진 case study 로, involving an anomaly인 경우 위의 그림 예시에서 1 FIT 001 PV에서 anomaly가 detect 됨. GDN에서는 1 MV 001 STATUS large deviation 이 일어나 이는 이상치 센서이거나 이와 연관됨을 알 수 있음.
GDN은 deviating sensor로부터 가장 attention weight이 높은 sensor를 indicate 함. 이는 높게 correlated 되어 있다는 것이고, GDN은 이런 anomalies를 predicted 및 observed sensor value를 비교함으로써 해석함
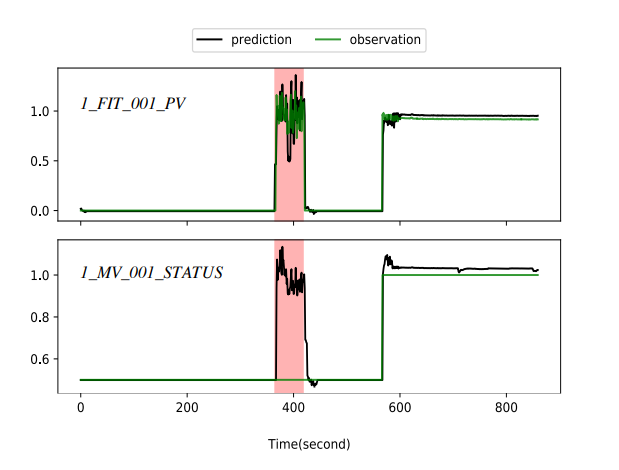
1 MV 001 STATUS에서 본 모델이 predicted an increase 했지만, 1 MV 001 STATUS에서 no change하였으므로, GDN에 의해 이상치라고 탐지됨
즉,
1) 우리의 모델은 anomaly score을 anomalies 를 localize하는데 도움을 줌
2) attention weight은 연관된 센서를 찾는데 도움을 줌
3) 각 센서의 predicted 행동을 비교하여 deviate from expectations이 얼마나 되는지를 알려줌
Conclusion
GDN approach를 통해 센서간의 relationship을 보았고, 패턴 사이의 deviation을 detect 함
2가지의 real-world 데이터를 통해 GDN이 baseline appraoch에 비해 outperform 함을 보여줌. 또한 이상치를 localize 하고 understand하는데 도움을 줌
추후 추가적인 아키텍쳐와 온라인 학습 방법을 통해 이 approach 의 실용성을 높이는 것이 필요함