JavaScript_동적 계획법(Dynamic Programming)_난이도 下

Eugenius1st·2022년 8월 31일

DP JavaScript

JavaScript_algorithm

목록 보기

5/21

동적 계획법(Dynamic Programming)_난이도 下

JavaScript_tiling

문제

세로 길이 2, 가로 길이 n인 2 x n 보드가 있습니다. 2 x 1 크기의 타일을 가지고 이 보드를 채우는 모든 경우의 수를 리턴해야 합니다.

풀이

dp 를 생각했으니 DFS와 헷갈렸다
하지만 배열에 담아서 이전값과 그 이전 값을 더하는 것임을 알았다.

코드

let tiling = function (n) {
  // TODO: 여기에 코드를 작성합니다. 2*n 크기의 보드
  // if (n === 2) return 2;
  // else if (n === 1) return 1;
  // else if (n === 0) return 0;
  // return tiling(n - 1) + tiling(n - 2);
  const tile = [1, 2];
  for (let i = 2; i <= n; i++) {
    tile[i] = tile[i - 1] + tile[i - 2];
  }
  return tile[n - 1];
};

배운것

이 문제는 경우의 수 문제이다

가로길이가 4까지의 경우

n이 1일 때) 하나의 경우의 수만 가능(|)
n이 2일 때) 두가지 경우의 수가 가능(| | , 二)
n이 3일 때) 세 가지 경우의 수가 가능(| | | , | 二 , 二 |)
n이 4일 때, 다섯 가지 경우의 수가 가능하다. (| | | | , | | 二 , | 二 | , 二二, | | 二)

여기서 주목해야 될 것은 n이 3일 때부터이다.
n = 3인 경우 안에 n=2인 경우의 모양이 분리해보면 포함되어있다.

(n=3인 경우의 첫 번째와 두 번째 경우에서 맨 왼쪽의 |를 빼고 생각하면 된다) 그리고 동시에 n=1인 경우 |가 포함되어있다.

(|)| | , (|)二

이것은 n = 4인 경우도 모양의 규칙성을 보면 n = 2인 경우와 n = 3인 경우가 포함되어있다는 것을 알 수 있다.

(|) | | | , (|) | 二 , (|) 二 | , (二) 二, (二)| |

이렇게 되는 이유는 세로의 길이는 고정된 상태로 가로의 길이가 늘어났기 때문에 쪼개면 결국 닮음 형태의 직사각형이 된다.

이러한 닮은 꼴은 재귀를 쓰면 간편해지고, 재귀 중에서 피보나치 수열과 매우 유사하다.

Naive Solution: O(2^N)

가장 만만하게 짤 수 있는 코드(내가 위에서 시간 복잡도 났던 코드)

 let tiling = function (n) {
   if (n <= 2) return n;
   return tiling(n - 1) + tiling(n - 2);
 };

이렇게 코드를 짜게 되면 시간복잡도가 지수함수가 되어, N이 커지면 실행 시간이 기하급수적으로 늘어난다.

따라서 최적화 기법을 사용하여 시간복잡도를 비약적으로 줄여야 한다.

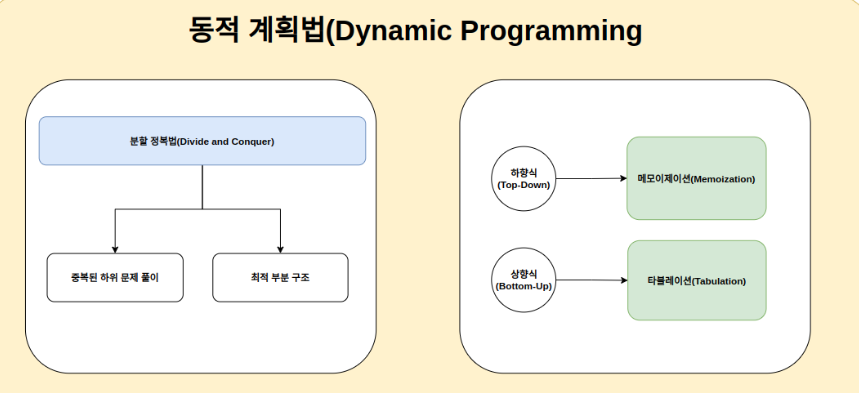
Memoiztion: O(N)

최적화 기법 중에서 가장 먼저 알아볼 것은 Memoization(메모이제이션)이다.

Memoization이란 '컴퓨터 프로그램이 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장하여 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술

let tiling = function (n) {
    const memo = [0, 1, 2];
    // 재귀를 위한 보조 함수(auxiliary function)
    const aux = (size) => {
      if (memo[size] !== undefined) return memo[size];
      if (size <= 2) return memo[n]; 
      // 이미 해결한 문제 이외의 것
      memo[size] = aux(size - 1) + aux(size - 2);
      return memo[size];
    };
    return aux(n);
  };

최적화 기법의 가장 큰 특징은 자기 자신의 함수를 리턴하는데, 리턴하는 함수는 오직 하나라는 점이다.

memo[size]를 보조함수의 더한 값으로 지정을 해주고, 이를 리턴한다.

Tabulation: O(N)

tabulation(태뷸레이션)이란 데이터를 테이블에 정리하면서 bottom-up 방식으로 해결하는 기법

내가 위 tiling에서 사용한 방법이다.

  let tiling = function (n) {
    const memo = [0, 1, 2];
    if (n <= 2) return memo[n];
    for (let size = 3; size <= n; size++) {
      memo[size] = memo[size - 1] + memo[size - 2];
    }
    return memo[n];
  };

태뷸레이션 방법의 특징은 반복문이다.
즉, 재귀를 사용하지 않는 것이다!

base case를 메모에 저장하는 것까지는 같다.
그 다음에는 재귀가 아니라 for문을 써서 recursive case를 해결하는 것이다.

반복문을 한번만 사용하기에, 시간을 줄어들지만, 재귀를 통해 줄이는 것이 더 간결!

Slicing window: O(N)

slicing window란 필요한 최소한의 데이터만을 활용하는 것

(재귀를 이용한 피보나치수열에서 꼬리재귀와 유사)

  let tiling = function (n) {
    let fst = 1,
      snd = 2;
    if (n <= 2) return n;
    for (let size = 3; size <= n; size++) {
      const next = fst + snd;
      fst = snd;
      snd = next;
    }
    return snd;
  };