하노이의 탑

문제

하노이 탑(Tower of Hanoi)은 퍼즐의 일종입니다. 세 개의 기둥과 이 기동에 꽂을 수 있는 크기가 다양한 원판들이 있고, 퍼즐을 시작하기 전에는 한 기둥에 원판들이 작은 것이 위에 있도록 순서대로 쌓여 있습니다. 게임의 목적은 다음 두 가지 조건을 만족시키면서, 한 기둥에 꽂힌 원판들을 그 순서 그대로 다른 기둥으로 옮겨서 다시 쌓는 것입니다.

한 번에 하나의 원판만 옮길 수 있습니다.
큰 원판이 작은 원판 위에 있어서는 안됩니다.
하노이 탑의 세 개의 기둥을 왼쪽 부터 1번, 2번, 3번이라고 하겠습니다. 1번에는 n개의 원판이 있고 이 n개의 원판을 3번 원판으로 최소 횟수로 옮기려고 합니다.

1번 기둥에 있는 원판의 개수 n이 매개변수로 주어질 때, n개의 원판을 3번 원판으로 최소로 옮기는 방법을 return하는 solution를 완성해주세요.

풀이

N개의 원판 중 N-1의 원판을 a기둥에서 b기둥으로 옮기고
남은 하나의 원판은 a기둥에서 c기둥으로 옮긴다. (베이스 조건)
먼저 옮겼던 N-1의 원판을 b기둥에서 a기둥으로 옮긴다.

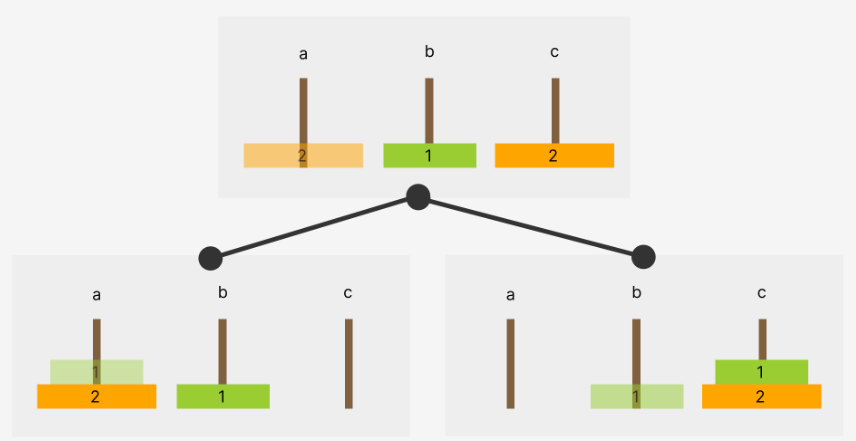
출력문 3번째 줄까지 위 그림과 같은 규칙을 가지고 구현되는 것을 볼 수 있다.
n은 원판의 갯수로 1번보다 작은 원판은 없으니까 num === 0 은 base case가 되겠다.

코드

function solution(n) {
	var answer = [];
 // 2^4-1 ==> 15
const hanoi = (num, from, other, to) => { //출발, 보조, 목적지
  if (num === 0) return
  hanoi (num - 1, from, to, other);
	answer.push([from,to]);
  hanoi (num - 1, other, from , to);  
}
	hanoi(n, 1, 2, 3)
  return answer
}