정렬(삽입,선택,버블) 알고리즘I

Eugenius1st·2022년 9월 20일

algorithm

JavaScript_algorithm

목록 보기

9/21

정렬(삽입,선택,버블) 알고리즘I

정렬이 필요한 이유

우리가 쓰는 소프트웨어를 생각해보자. 곳곳에 정렬이 들어가지 않은 곳이 없다.

내 메일 보관함은 도착 시간 기준으로 정렬돼있다.
배달앱을 켜면 음식점이 인기순, 판매량순, 배달빠른 순으로 정렬된다.
구글에 검색어를 입력하면 가장 관련있는 페이지 순으로 정렬된다.
지도 앱에서 음식점을 검색하면 가까운 거리 순으로 정렬된 결과를 보여준다.
페이스북은 내가 좋아할만한 게시물 순으로 뉴스피드를 정렬한다.
트위터 피드. 인스타 스토리... 손 아프니까 이하 생략.
그 외에 우리 눈에 보이지 않는 수많은 정렬까지.

정렬은 어디에나 있다.
스크롤 한번, 클릭 한번이 다 정렬이다.

어떤 문제를 해결할 때 정렬 여부가 큰 영향을 미치는 경우가 있다.
정렬이 되어 있으면 훨씬 간단하고 효율적으로 풀 수 있게 되는 것이다.
예를 들면 아래와 같은 경우 매우 유용하다.

분포도의 중위값을 알아내고자 할 때
데이터에서 중복값을 잡아내고 싶을 때
이진 탐색을 할 때

단, 정렬을 하는데에도 비용이 들기 때문에 정렬로 얻을 수 있는 이점이 비용보다 클 것인지를 따져보고 적용해야한다.

정렬 알고리즘의 종류

정렬 알고리즘은 여러가지가 있다

버블정렬 (Bubble Sort)
선택정렬 (Select Sort)
삽입정렬 (Insertion Sort)
병합정렬 (Merge Sort)
퀵 정렬 (Quick Sort)

정렬 '방식'들을 알아야하는 이유

언어마다 정렬을 해주는 메소드가 존재한다. 자바스크립트에서는 sort() 메소드가 있고 파이썬에도 sort()와 sorted()가 있다. 내장 메소드만으로 정렬이 가능한데 왜 여러 종류의 정렬 알고리즘을 알아야 하는것일까?

그 이유는 내장 메소드의 정렬 알고리즘이 늘 최선의 퍼포먼스를 보장하지는 않기 때문이다.
데이터의 양이나 상황에 따라 적합한 정렬 알고리즘을 직접 구현하여 사용하는 것이 더 높은 효율을 낼 수 있다.

정렬은 구현 및 시간복잡도 등 디테일 하게 아는 것이 중요하다.

=> 위 사항을 알아야 하는 이유?

단순히 정해진 알고리즘에 정해진 코드를 짜는 사람이 아니라, 주도적으로 코드의 알고리즘 설계, 분석 / 문제점 파악 등을 명확히 하려면,

아래의 정렬 정도는 손쉽게 짜고, 시간복잡도 또한 분석할 줄 알아야 한다고 생각한다.

https://www.toptal.com/developers/sorting-algorithms

또한, 초기에 어떤 순서대로 되어있느냐에 따라, 정렬 시간이 달라진다.

정렬 알고리즘

정렬 알고리즘이란 원소들을 일정한 순서대로 열거하는 알고리즘이다.

정렬 알고리즘은 다양한 알고리즘들이 있다. 이번 포스팅에 들어갈 버블 정렬, 선택 정렬, 삽입 정렬 이외에도 합병 정렬, 퀵 정렬, 힙 정렬 들이 있지만 기본적으로 버블/선택/삽입을 제외한 알고리즘은 어려운 편에 속하므로 먼저 세 가지 알고리즘에 대해 공부하자!

정렬의 기본이다! -> 버블, 선택, 삽입 정렬

버블 정렬 (Bubble Sort)

버블 정렬은 정렬하는 모습이 거품이 꺼지는 모습과 비슷하기 때문에 붙여진 이름이라고 한다. 아마 가장 처음 배우는 정렬 알고리즘이 될 것이고, 별로 좋은 알고리즘이 아니기에 실전에서는 잘 사용되지 않는다. 하지만 이해하기는 제일 쉽다.

간단히 말하면, 현재 배열 요소와 그 다음 배열 요소를 비교해 왼쪽이 오른쪽보다 크면 교환한다. 그림으로 보자.

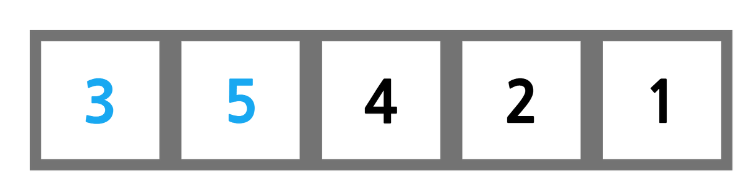
위 그림에서 3과 5를 비교했을 때, 3이 5보다 작으므로 둘은 교환하지 않는다.

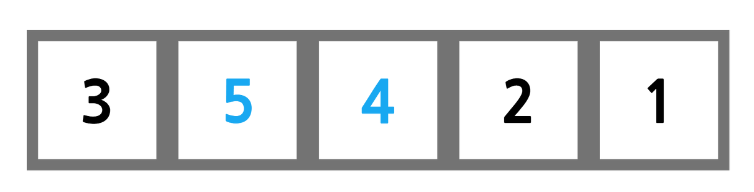
다음으로 넘어가 5와 4를 비교했을 때, 5가 4보다 크므로 둘이 교환한다.

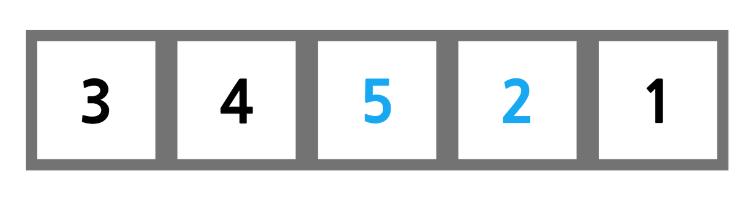
또다시 다음으로 넘어가 5가 2보다 크므로 둘이 교환한다.

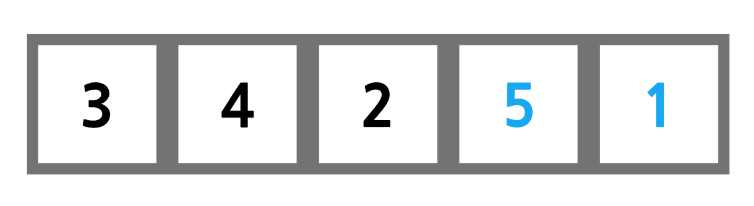
5가 1보다 크므로 둘이 교환한다.

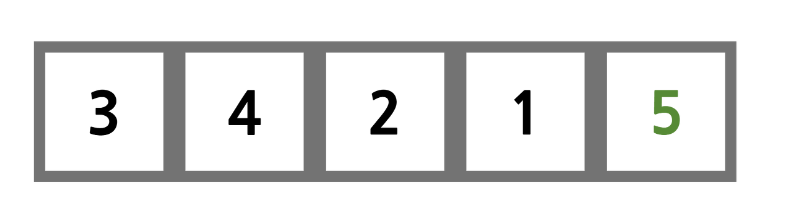
첫 번째 과정을 끝마쳤을 때, 배열에서 가장 큰 수였던 5가 가장 뒤로 이동되었다. 이후에는 이 과정을 반복해주면 된다.

버블 정렬 장점
에 메모리가 절약된다는 점, 구현하기 쉽다는 점, 그리고 이미 정렬된 데이터를 순회하는 경우 O(n)번만 순회하면 된다!
버블 정렬 단점
배열의 크기가 N이라 했을 때, N - 1개의 아이템과 비교해야 한다. 헌데 최악의 경우에는 모든 아이템을 교환해야 하므로 버블 정렬의 시간 복잡도는 O(n^2)이다.!!

Python

def BubbleSort(arr):
    for i in range(len(arr) - 1, 0, -1):
        for j in range(i):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j] # Swap의 간편화

버블 정렬 단점 개선 코드

function bubbleSort (array) {  
  for (let i = 0; i < array.length; i++) {    
    let swap;    
    for (let j = 0; j < array.length - 1 - i; j++) {      
      if (array[j] > array[j + 1]) {        
        swap = array[j];        
        array[j] = array[j + 1];        
        array[j + 1] = swap;      
      }    
    }    
    if (!swap) break;
  }  
  return array;
}
console.log(bubbleSort([5, 4, 3, 2, 1]));

버블정렬 시간 복잡도

Big O

Worst Case: O(n^2): 정렬이 하나도 안되어있는 경우

Best Case: O(n): 이미 정렬이 되어있는 경우

버블 정렬은 최악의 경우에 O(n^2)의 시간 복잡도를 가진다. 왜냐하면 각 자리를 찾기 위해서 n번의 순회를 해야하며 n번의 회전 동안에 요소의 개수만큼 또 순회를 해야하기 때문이다. 그러나 이미 정렬이 되어있는 경우에는 한 번의 순회로 정렬 여부를 알 수 있다.

삽입 정렬 (Insertion Sort)

삽입 정렬은 정렬 범위를 1칸씩 확장하며 새롭게 정렬 범위에 들어온 값을 기존 값들과 비교해 알맞은 자리에 삽입한다. 즉, 가면 갈수록 왼쪽은 이미 정렬된 부분이고 오른쪽은 정렬되지 않은 부분이므로 정렬할 부분의 원소를 이미 정렬된 부분에 하나씩 삽입하는 것이다. 그림으로 보자.

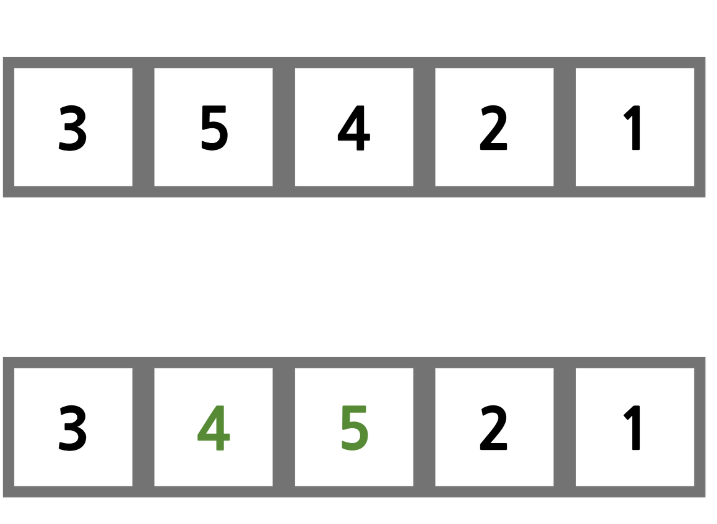
삽입 정렬은 인덱스 1번부터 시작한다. 즉, 값 5부터 시작한다. 3과 5는 이미 정렬되어 있으므로 건드리지 않는다. 다음 과정에서 4는 5보다 작으므로 서로 교환한다. 또한 3은 4보다 작으므로 다음 사이클로 넘어간다.

2는 5보다 작으므로 교환하고, 2는 4보다 작으므로 교환하고, 2는 3보다 작으므로 교환한다. 해당 과정을 끝까지 마치면 1도 맨 앞으로 이동되며 자연스레 오름차순 정렬이 될 것이다.

잘 보면 전체적은 범위는 정방향으로 늘어나지만, 정렬하는 과정 자체는 역방향인것을 알 수 있다. 또한 삽입 정렬은 필요한 요소만 스캔하지만 선택 정렬은 모든 요소를 스캔하므로 통상적으로는 삽입 정렬이 선택 정렬보다 빠르다.

장점
삽입 정렬도 버블 정렬과 같이 in place 알고리즘이기 때문에 메모리가 절약된다는 장점이 있다.
또한 구현하기 매우 쉽고 이미 정렬된 데이터를 순회하는 경우 O(n)번만 순회하면 되기 때문에 정렬이 되었는지 안되었는지 테스트하는 용도로 사용될 수 있다.
단점
삽입 정렬 역시 가장 큰 단점은 자료의 개수가 많아질수록 성능이 매우 떨어진다는 점이다

Python
def InsertionSort(arr):
    for i in range(1, len(arr)):
        for j in range(i, 0, -1): # 안쪽은 역방향
            if arr[j - 1] > arr[j]:
                arr[j - 1], arr[j] = arr[j], arr[j - 1] # Swap의 간편화

삽입 정렬 단점 개선 코드

function insertionSort (array) {  
  for (let i = 1; i < array.length; i++) {    
    let cur = array[i];    
    let left = i - 1;     
    while (left >= 0 && array[left] > cur) {      
      array[left + 1] = array[left];      
      array[left] = cur;      
      cur = array[left];      
      left--;    
    }  
  }  
  return array;
}

삽입정렬 시간복잡도

Big O
Worst Case: O(n^2): 정렬이 하나도 안되어있는 경우
Best Case: O(n): 이미 정렬이 되어있는 경우

삽입 정렬 역시 버블 정렬과 똑같은 시간 복잡도를 가진다.

선택 정렬 (Selection Sort)

선택 정렬은 가장 작은 아이템의 위치를 다른 변수에 저장해둔 후 첫 번째 자리에 다른 변수에 있던 값을 넣는다. 다음 과정에서는 두 번째 자리에 다음으로 작은 값을 넣고, 배열을 전부 돌 때까지 반복한다. 그림으로 보자.

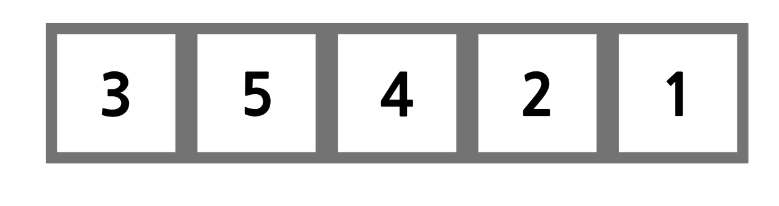
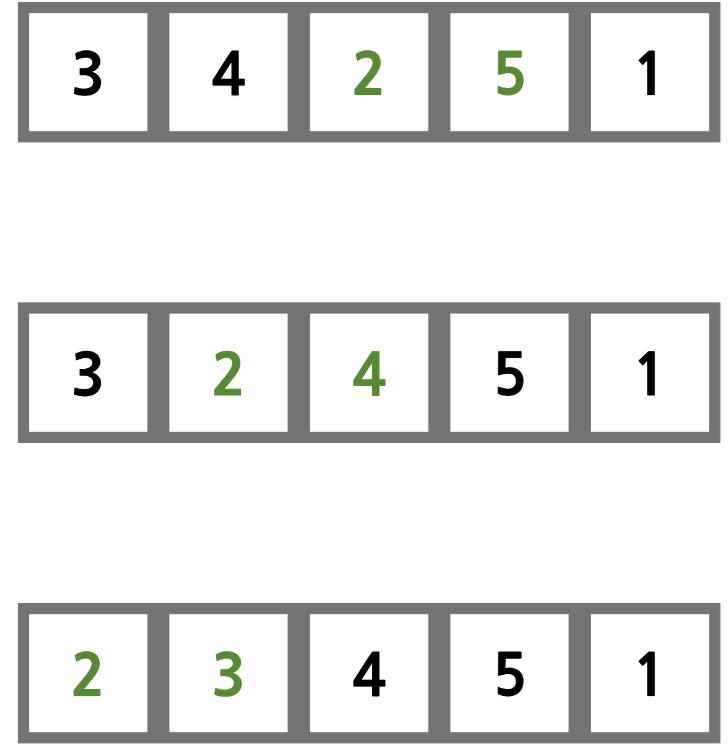
처음에 3이 있는 자리를 i라고 놨을 때, j는 i 다음 인덱스부터 가장 작은 수의 인덱스를 탐색한다. 이를 minidx라고 하자.

위 그림에서는 1이 가장 작으므로 minidx는 4이므로, 배열 인덱스 0과 인덱스 4의 자리를 바꾼다.

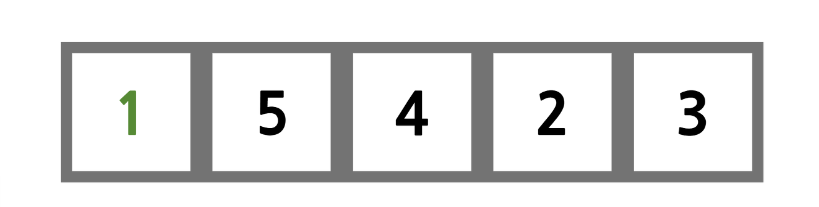
1과 3의 자리가 바뀌었다. 첫 번째 과정을 마쳤으므로, 이번에는 2가 가장 작은 수이므로 배열 인덱스 1과 3의 자리를 바꾼다.

해당 과정을 끝까지 반복해주면 자연스레 오름차순으로 정렬이 된다.

선택 정렬은 버블 정렬과는 다르게 N번의 교환을 하지 않는다. minidx를 저장해 놓아 매 과정마다 한 번만 교환하므로 선택 정렬이 버블 정렬보다 더 나은 알고리즘이라고 할 수 있다.

장점
선택 정렬도 위의 두 정렬과 같이 in place 알고리즘이기 때문에 메모리가 절약된다는 장점이 있으며 알고리즘이 직관적이므로 이해하기도 쉽고 구현하기도 쉽다.

단점
선택 정렬은 최선의 경우에도, 최악의 경우에도 O(n^2)의 시간이 걸리는 만큼 성능이 매우 떨어진다.

Python

def SelectionSort(arr):
    for i in range(len(arr) - 1):
        minidx = i
 
        for j in range(i + 1, len(arr)):
            if arr[j] < arr[minidx]:
                minidx = j
 
    	arr[i], arr[minidx] = arr[minidx], arr[i] # Swap의 간편화

function selectionSort (array) {  
  for (let i = 0; i < array.length; i++) {    
    let minIndex = i;    
    for (let j = i + 1; j < array.length; j++) {      
      if (array[minIndex] > array[j]) {        
        minIndex = j;      
      }    
    }    
    if (minIndex !== i) {      
      let swap = array[minIndex];      
      array[minIndex] = array[i];      
      array[i] = swap;
    }    
    console.log(`${i}회전: ${array}`);  
  } 
  return array;
}
console.log(selectionSort([5, 4, 3, 2, 1]));