• 수많은 반복의 연속
  • Layer
  • 하나의 레고 블록 정의 후 계속 연결
• 블록 반복의 연속
  • Encoder layer/ Decoder layer
  • ResNet

torch.nn.Module

• 딥러닝을 구성하는 Layer의 base class
• input, output, forward or backward(Autograd > weight) 정의 필요
• 학습의 대상이 되는 parameter(tensor) 정의

nn.Parameter

• Tensor 객체의 상속 객체
• nn.Module 내에 attribute가 될 때는 required_grad=True로 지정(>AutoGrad의 대상)되어 학습 대상이 되는 Tensor
• 우리가 직접 지정할 일은 잘 없음: 대부분의 layer에는 weights 값들이 지정되어 있음

class MyLiner(nn.Module):
	def __init__(self, in_features, out_features, bias =True):
	# 만약 3개의 배치 데이터에서 7개의 feature을 넣어 5개의 output을 가진다면
	# (input) 3*7 > (weight) 7*5 > (output) 3*5
		super().__init__()
		self.in_features=in_features    # 7개
		self.out_features=out_features  # 5개
		
		self.weights=nn.Parameter(    # 7*5 크기의 parameter(weight)값 지정
				torch.randn(in_features, out_features))

		self .bias=nn.Parameter(torch.randn(out_features)) # XW+b에서 b에 해당

def forward(self, x :Tensor):    # Tensor로 구해진 x의 값
	# 기본적인 formula(XW+b) 구현
	return x @self.weights + self.bias   # self.bias: 일종의 y_hat

Parameter vs Tensor

weights를 parameter로 설정해줌> 학습의 대상이 되는 파라미터: layer.parameters() > 학습에 대한 parameter들의 현재 각각 weight 값 random 하게
gradient 대상이 되는지 아닌지도 지정(requires_grad=True)
나중에 backward propagation이 일어났을 때 미분이 되는 값들임

만약 parameter가 아님 Tensor로 선언했다면 방식은 비슷하지만 layer.parameters()를 찍으면 나오지 않음. parameter는 미분의 대상이 되는 것만 보여 줄 수 있음(backward propagation의 대상이 아닌 것들은 출연하지 않음)

Backward

• layer에 있는 parameter들의 미분을 수행
• Forward의 결과값 (model의 output=예측치)(y_hat을 forward함수에 넣어줌)과 실제값간의 차이(loss)에 대해 미분을 수행 Autogradient 자동미분으로 연산 (backward 함수 호출됨)
• 해당 값으로 parameter 업데이트

for epoch in range(epochs):    # epoch이 돌아갈 때마다!
	…… 
	# Clear gradient buffers because we don't want any from previous epoch to carry forward
	optimizer.zero_grad()    # optimizer를 zero gradient로 바꿔줌 (초기화)
	
	# get output from the model, given inputs
	outputs=model(inputs)    # model에 input값을 넣으면 y_hat 출력

	# get loss for the predicted output
	loss=criterion(outputs, labels)    # outputs: y_hat, labels: y 들의 loss값 구함 
	print(loss)
	# get gradients w.r.t to parameters
	loss.backward()    # ( {\delta loss}/{\delta W} )

	# update parameters
	optimizer.step()    # 한번에 weight 업데이트
	…… 

4단계 기억하기!

1. optimizer.zero_grad()
2. loss=criterion(outputs, labels)
3. loss.backward()
4. optimizer.step()

Backward from the scratch

• 실제 backward는 Module 단계에서 직접 지정가능
  : but 할 필요 x autogradient가 해줌
• module에서 backward와 optimizer오버라이딩
• 사용자가 직접 미분 수식을 써야하는 부담 (layer가 여러개라면..?)
  → 쓸일은 없으나 순서는 이해할 필요는 있음

Logistic Regression

logistric regression은 sigmoid fuction의 원래 z값에 x와 \theta : weight에 linear combination을 넣으 준 것

• sigmoid function $\frac{1}{1+e^{-z}}$

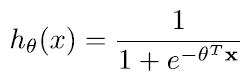
class LR(nn.Module):
	def __init__(self, dim, lr=torch.scalar_tensor(0.01)):
		super(LR, self).__init__()
		# intialize parameters
		self.w = torch.zeros(dim, 1, dtype=torch.float).to(device)
		self.b = torch.scalar_tensor(0).to(device)
		self.grads = {"dw": torch.zeros(dim, 1, dtype=torch.float).to(device),
				"db": torch.scalar_tensor(0).to(device)}
		self.lr = lr.to(device)

	def forward(self, x):    # hyperdash fucntion (sigmoid) : y_hat을 구하는 것
		## compute forward
		z = torch.mm(self.w.T, x)    # 좀 더 정확하게 하려면 z = torch.mm(self.w.T, x) + w.b
		a = self.sigmoid(z)
		return a

	def sigmoid(self, z):
		return 1/(1 + torch.exp(-z))
	
	def backward(self, x, yhat, y):
		## compute backward
		# 미분값을 적어줌
		self.grads["dw"] = (1/x.shape[1]) * torch.mm(x, (yhat - y).T)    # 밑의 수식에서 yhat = h_{theta}(x^i)
		self.grads["db"] = (1/x.shape[1]) * torch.sum(yhat - y)    # x_i^j가 1
	
	def optimize(self):
		## optimization step
		# 기존의 theta, W의 값의 미분값만큼 update
		self.w = self.w - self.lr * self.grads["dw"]
		self.b = self.b - self.lr * self.grads["db"]

• backward
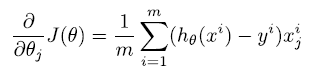  cost fuction 미분해주면 위와 같이 나옴 ($\frac{\delta L }{\delta W}$ : W에 대해 미분)
  bias에 대해 미분해주면 위와 같이 나옴