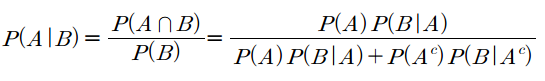Bayes Theorem (베이즈 정리)

참고

사전확률과 사후확률의 관계를 나타내는 정리로, 새로운 정보를 토대로 어떤 사건이 일어났다는 주장의 신뢰도를 갱신해나가는 방법이다.

$P(H|E) = \frac{P(E|H)P(H)}{P(E)}$

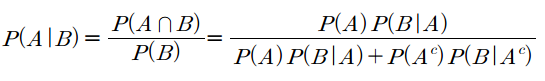
조건부 확률이다. 처음엔 조건부 확률과 증거, 주장, 가능도 이런 게 무슨 관련이 있는거지? 싶었다.

우선 사전확률, 사후확률, 가능도에 대해 알아보자.

사전 확률 : 어떤 사건이 일어났다는 주장의 신뢰도, 특정 사건의 확률

사후 확률 : 새로운 정보가 발견되었을 때의 어떤 사건이 일어났다는 주장의 신뢰도

가능도 : 어떤 사건이 일어났을 때 그러한 증거가 보일 가능성

예제를 통해 살펴보자.
H(Hypothesis) : 실제로 병이 있다.
E(Evidence) : 양성판정을 받았다.

병의 발병률은 0.001이고, 실제 양성인데 양성판정을 받을 확률은 0.99, 실제 음성인데 음성판정을 받을 확률은 0.98이다.

$P(H)=0.001$ 사전확률

$P(E|H)=0.99$ 가능도

$P(E^c|H^c) = 0.98$ -> $P(E|H^c) = 0.02$

$P(H|E) = \frac{P(E|H)P(H)}{P(E)} = \frac{P(E|H)P(H)}{P(E|H)P(H)+P(E|H^c)P(H^c)}$

$P(H|E) = \frac{P(E|H)P(H)}{P(E|H)P(H)+P(E|H^c)P(H^c)} = \frac{0.001\times 0.99}{0.001\times 0.99 + 0.999\times 0.02}$