Eigen value, Eigen vector

$Av = λv$

v를 A로 선형변환했을때 방향은 바뀌지 않고 크기만 변하게 하는 v와 λ를 eigen vector, eigen value라고 한다.

위의 식을 변형하면

$(A-λI)v = 0$

$A-λI$의 역행렬이 존재하면 v는 0이어야한다. v는 0이 아니기때문에 $A-λI$는 역행렬이 존재하지 않아야한다. det($A-λI$) = 0 를 이용하면 eigen value, eigen vector를 구할 수 있다.

그 과정은 다음과 같다.

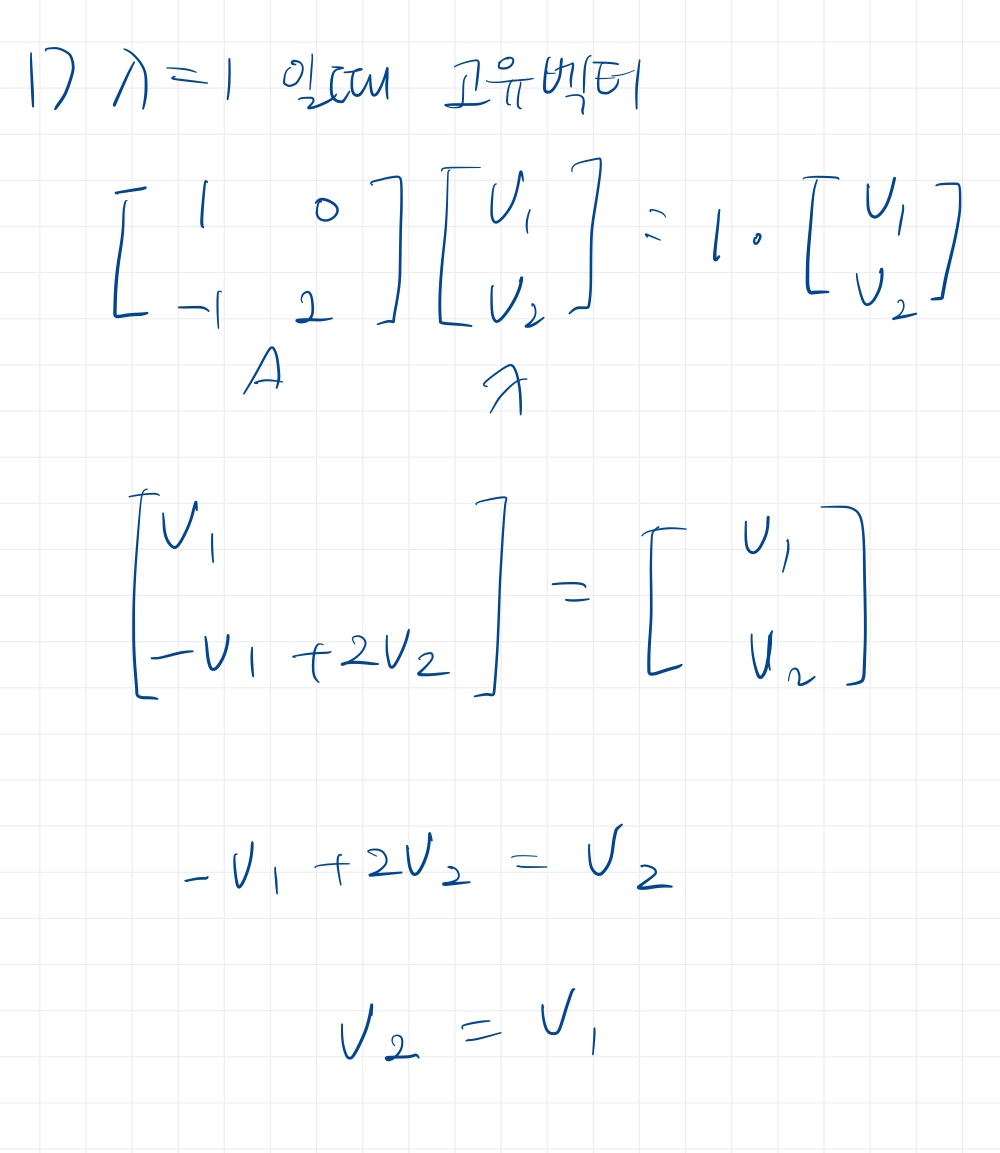
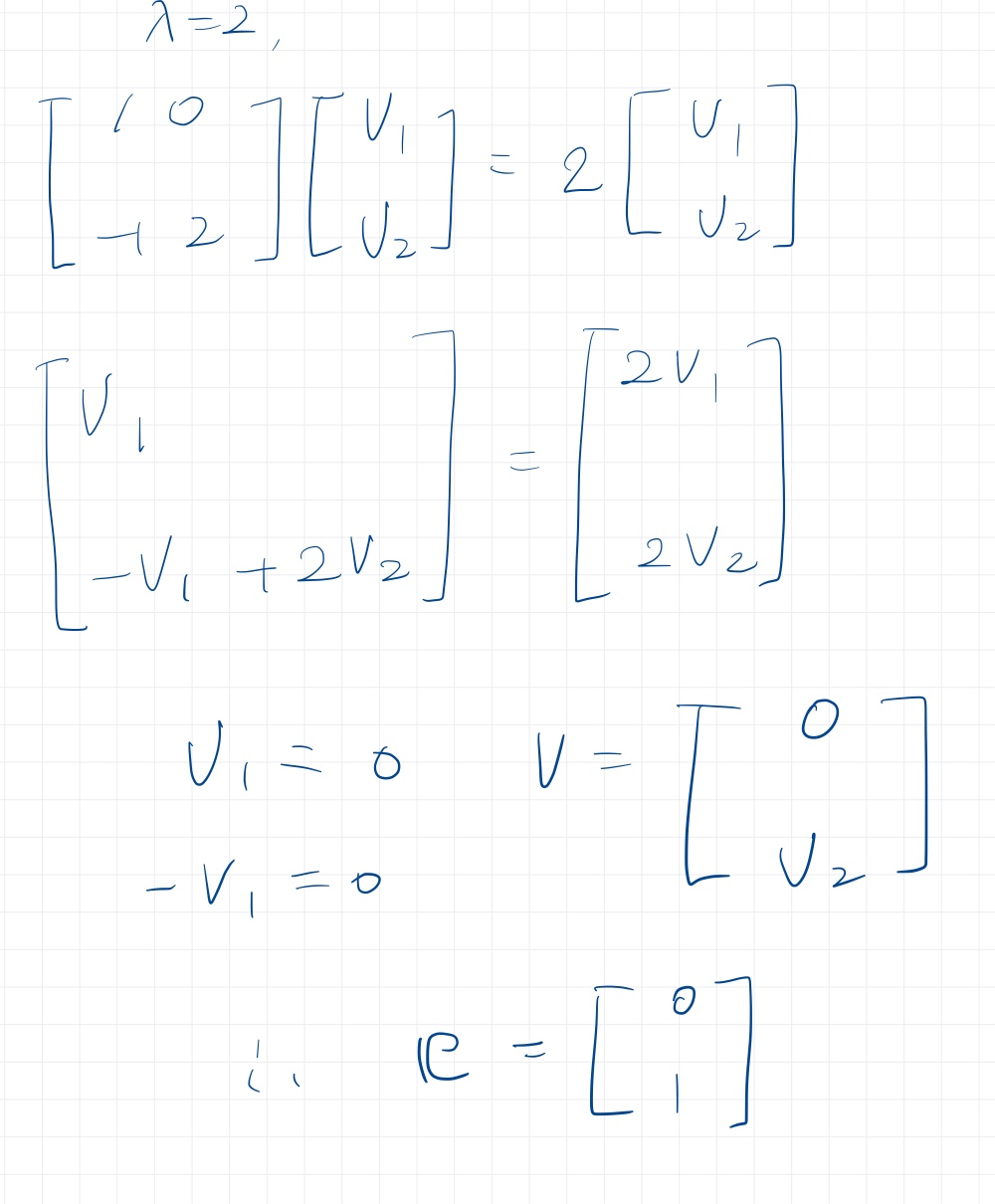
Eigen decomposition

여러개의 eigen vector가 존재, 이를 한꺼번에 나타내면 아래와 같음

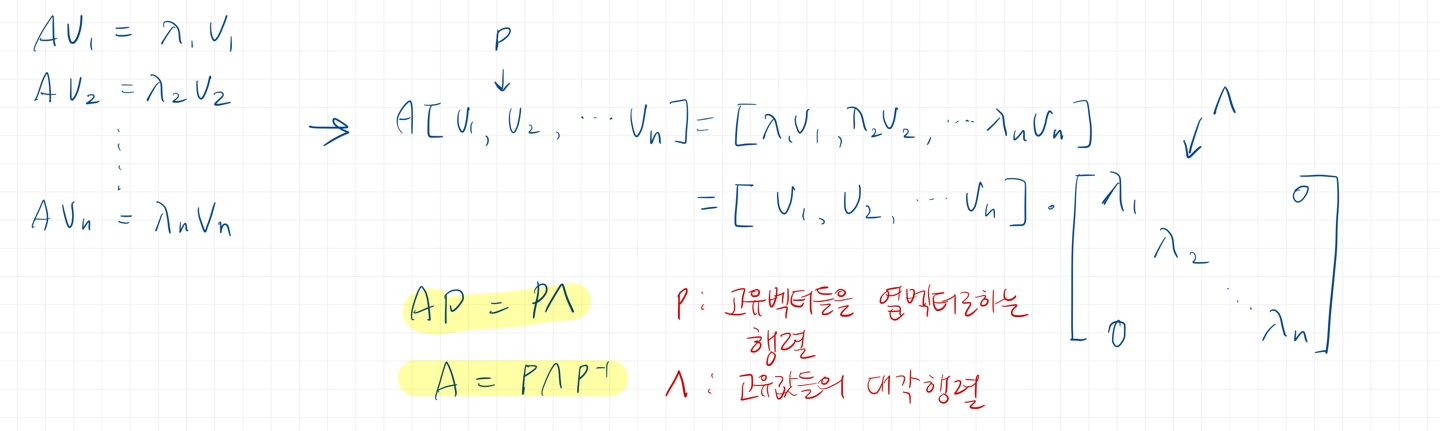
A가 고유벡터를 열벡터로 하는 행렬 P와 고유값을 대각원소로하는 대각행렬 Λ, P의 역행렬로 분해된다.

PCA

데이터의 특성을 나타내는 공분산 행렬의 eigen value, eigen vector를 구해서 큰 eigen value를 가지는 상위의 eigen vector들의 공간으로 projection하는 것이다.

고차원의 피쳐공간을 데이터의 분산을 가장 잘 설명하는 몇개의 벡터들의 공간인 저차원으로 투영하여 차원의 저주를 피할 수 있게한다.

더 자세히 설명해놓은 게시물
PCA를 소개합니TADA~🎉