딥러닝 기초 - 딥러닝에서의 데이터 표현

딥러닝에서의 데이터 표현

• 텐서 : 텐서는 데이터를 위한 컨테이너
  -> 텐서는 임의의 차원의 개수를 가지는 행렬의 일반화된 모습
  -> 텐서에서는 차원(dimension)을 종종 축(axis)이라고 부름
  
• 랭크 : 텐서의 축 개수 (독립인 벡터의 갯수)

4d - tensor 부터는 3d-tensor를 쌓아올렸고, 7d-tensor를 표현하고 싶으면,
6d-tensor를 쌓아올리면 될 것이다.

벡터말고도 스칼라라는 개념이 있다.
스칼라는 0차원 텐서이며 하나의 숫자만을 담고 있다.

벡터는 하나의 축을 가진다.

행렬(matrix)는 2d-tensor이며, 2개의 축이 있고, 이것을 행과 열이라고 부른다.
이것은 숫자가 채워진 사각 격자라고 할 수 있다.

3d-tensor는 직육면체 형태로 해석할 수 있다.
딥러닝에서는 보통 4d-tensor까지 다루며, 동영상 데이터는 5d-tensor까지 가기도 한다.

축의 개수(rank)에 대해서 알아보면, 행렬에서는 2개의 축, 직육면체 형태는 3d-tensor에서는 3개의 축이 있다는 것을 알 수 있다.

행렬의 크기는 아래와 같이 볼 수 있다.
아래의 코드를 보자

import numpy as np

# 스칼라
scalar = np.array(5)
print("스칼라:", scalar)
print("Shape:", scalar.shape)
print("Rank:", scalar.ndim)

# 1D 텐서 (벡터)
vector = np.array([1, 2, 3, 4, 5])
print("\n1D 텐서 (벡터):", vector)
print("Shape:", vector.shape)
print("Rank:", vector.ndim)

# 2D 텐서 (행렬)
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print("\n2D 텐서 (행렬):", matrix)
print("Shape:", matrix.shape)
print("Rank:", matrix.ndim)

# 3D 텐서
tensor3d = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
print("\n3D 텐서:", tensor3d)
print("Shape:", tensor3d.shape)
print("Rank:", tensor3d.ndim)

결과는 위와 같다.

텐서 연산

컴퓨터 프로그램에서 이진수 형태의 입력을 처리하는 이항 연산들(and,or,nor 등)과 같이 심층 신경망의 입력에 해당하는 텐서에 대해서도 연산을 수행할 수 있다.

• 원소별 연산
• 브로드 캐스팅
• 텐서 점곱
  각각의 설명은 아래와 같다.

원소별 연산 (Element-wise Operations): 이 연산은 텐서의 각 원소에 독립적으로 적용됩니다.
브로드캐스팅 (Broadcasting): 서로 다른 크기의 배열에서 연산을 수행할 때 자동으로 크기를 맞추는 기능입니다.
텐서 점곱 (Tensor Dot Product): 두 텐서 간의 점곱(행렬 곱)을 계산합니다.

import numpy as np

# 원소별 연산
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
elementwise_addition = a + b  # 원소별 덧셈
elementwise_multiplication = a * b  # 원소별 곱셈

print("원소별 덧셈:", elementwise_addition)
print("원소별 곱셈:", elementwise_multiplication)

# 브로드캐스팅
a = np.array([1, 2, 3])
b = 2
broadcasted_multiplication = a * b  # 스칼라와 벡터의 곱셈

print("\n브로드캐스팅된 곱셈:", broadcasted_multiplication)

# 텐서 점곱 (행렬 곱)
a = np.array([[1, 2], [3, 4]])
b = np.array([[2, 0], [1, 2]])
tensor_dot_product = np.dot(a, b)  # 행렬 곱

print("\n텐서 점곱 결과:\n", tensor_dot_product)

해당 결과는 이와 같다.

더 심화된 예시는 아래와 같다.
딥러닝에서 자주 볼 수 있는 최적화 함수 relu 연산도 하나의 텐서에 대해 이루어질 수 있다.

import numpy as np

# ReLU 함수 정의
def relu(x):
    return np.maximum(0, x)

# 배열 정의
array = np.array([-3, -1, 0, 2, 4])

# 원소별로 ReLU 함수 적용
relu_applied = relu(array)

print("원본 배열:", array)
print("ReLU 적용 후:", relu_applied)

이 예시로 하나의 텐서 x의 원소들에 대해 음수인 원소들을 0으로 치환한다.

브로드캐스팅(Broadcasting)

python에서 가장 중요하다고 볼 수 있는 브로드캐스팅에 대해 깊게 공부할 필요가 있다.

차원이 맞지 않는 텐서에 대해 텐서 연산을 수행하고자 하였을 때 발생하는 가상의 연산.

• 큰 텐서의 차원(ndim)에 맞도록 크기가 작은 텐서에 새로운 축이 추가됨
• 새 축을 따라서 큰 텐서의 크기와 맞을 때까지 작은 텐서를 확장함

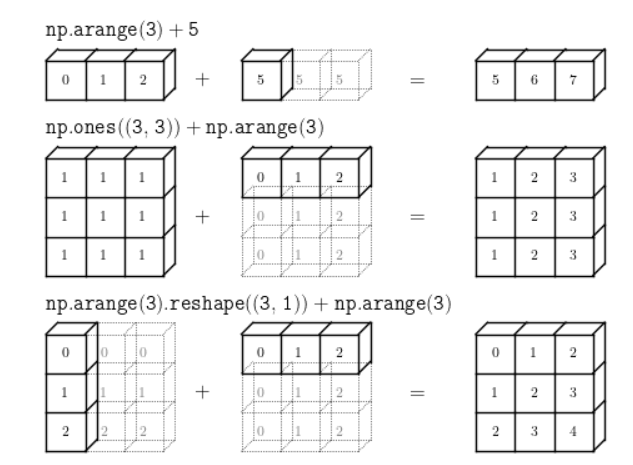
출처: http://www.astroml.org/book_figures/appendix/fig_broadcast_visual.html

import numpy as np

# 2차원 텐서 (행렬) 정의
matrix = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]
])

# 1차원 텐서 (벡터) 정의
vector = np.array([1, 0, -1])

# 브로드캐스팅을 이용한 덧셈
result = matrix + vector

print("행렬:")
print(matrix)
print("\n벡터:")
print(vector)
print("\n브로드캐스팅 후 덧셈 결과:")
print(result)

텐서 점곱(tensor product)
원소별 연산의 곱셈이 아닌 입력 텐서의 원소들을 결합시키는 연산을 수행함(행렬의 곱셈과 유사하다)

• 2d-tensor에 해당하는 행렬에서의 점곱(dot product) 다이어그램: 어떤 크기의 점곱이 가능한지 확인할 수 있음.

import numpy as np

# 두 행렬 정의
A = np.array([
    [1, 2],
    [3, 4]
])
B = np.array([
    [2, 0],
    [1, 3]
])

# 텐서 점곱
dot_product = np.dot(A, B)

print("행렬 A:")
print(A)
print("\n행렬 B:")
print(B)
print("\n텐서 점곱 결과:")
print(dot_product)


# reshape - 텐서의 크기 변환
print()
print("\n텐서 reshpape결과:" ,dot_product.reshape(1,4))

reshape 함수는 원본 데이터를 유지하면서 배열의 차원과 크기를 변경할 수 있다.

딥러닝에서의 기하학적 해석

딥러닝 모델, 특히 신경망은 본질적으로 데이터를 고차원에서 저차원 공간으로 변환하는 함수의 집합으로 볼 수 있습니다. 이 변환은 여러 층(layer)을 통해 점진적으로 이루어지며, 각 층은 텐서 연산(예: 선형 변환, 비선형 활성화 함수)을 사용하여 입력 데이터를 변형합니다.

• 선형 변환 (Linear Transformation): 데이터를 다른 차원으로 회전하거나 스케일링하는 기본적인 변환입니다.
• 비선형 변환 (Non-linear Transformation): ReLU 같은 활성화 함수가 주로 사용되며, 이를 통해 모델은 비선형적인 복잡성을 학습할 수 있습니다.

import numpy as np
import matplotlib.pyplot as plt

# 2차원 입력 데이터 생성
points = np.random.rand(300, 2) * 2 - 1  # -1과 1 사이의 무작위 점들

# 선형 변환 (회전)
theta = np.pi / 4  # 45도 회전
rotation_matrix = np.array([
    [np.cos(theta), -np.sin(theta)],
    [np.sin(theta), np.cos(theta)]
])
rotated_points = points @ rotation_matrix  # 행렬 곱을 사용한 점들의 회전

# 비선형 변환 (ReLU 적용)
relu_transformed_points = np.maximum(rotated_points, 0)

# 시각화
plt.figure(figsize=(12, 4))
plt.subplot(1, 3, 1)
plt.scatter(points[:, 0], points[:, 1], alpha=0.6)
plt.title("Original Data")
plt.axis('equal')

plt.subplot(1, 3, 2)
plt.scatter(rotated_points[:, 0], rotated_points[:, 1], alpha=0.6)
plt.title("After Linear Transformation")
plt.axis('equal')

plt.subplot(1, 3, 3)
plt.scatter(relu_transformed_points[:, 0], relu_transformed_points[:, 1], alpha=0.6)
plt.title("After Non-linear Transformation (ReLU)")
plt.axis('equal')

plt.show()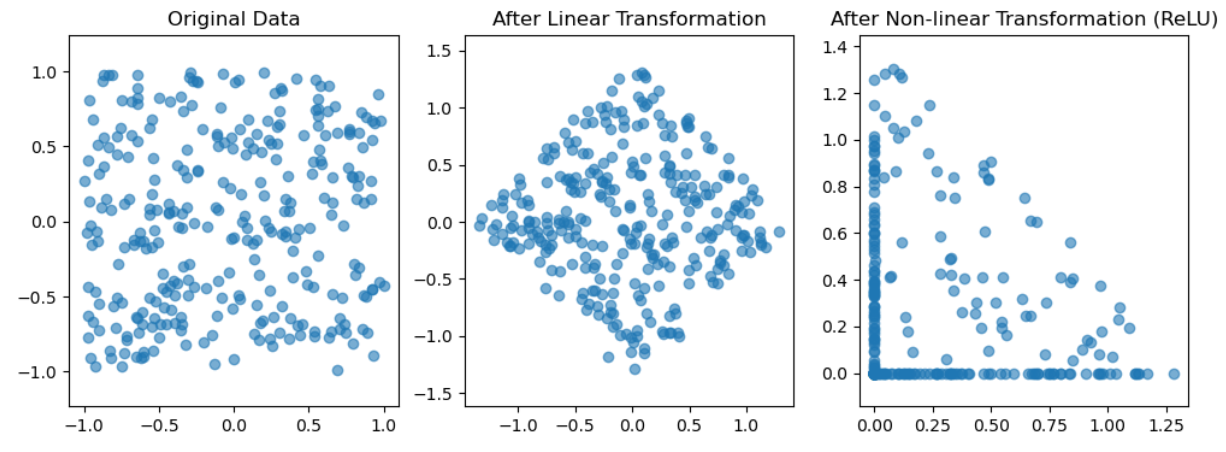

딥러닝에 대한 기하학적 해석이 가능한데, 신경망은 텐서 연산들의 연쇄를 통해 구성되었으며, 모든 텐서 연산은 입력 데이터에 대한 기하학적 변환으로 쉽게 해석될 수 있다.
또한, 심하게 꼬여있는 데이터의 매니폴드에 대한 깔끔한 표현(=패턴)을 찾는 것을 목표로 합니다.