딥러닝 기초 - 최적화

박종일·2024년 4월 23일

딥러닝

딥러닝기초

목록 보기

3/5

그래디언트 디센트(Gradient Descent)

기본 개념 : 실수 x를 새로운 실수 y로 매핑하는 미분 가능한 y=f(x)를 고려할 때, 특정한 점 p에서의 도함수를 의미함.

그래디언트 값이 큰 입력 값의 볂화는 함수 값에 대해서도 큰 변화를 야기하며, 그래디언트의 방향과 크기를 고려하여 입력 값을 이동시키는 것이 손실함수를 줄이는데, 효울적이다.

반복적으로 그래디언트 반대 방향으로 입력값을 이동시키며 속성 공간에 대한 탐색을 수행할 수 있다.

이는 최적해를 찾는 수치적 방법에 이용할 수 있다. 예시로 뉴턴 메소드(Newton's method)가 있다.

뉴턴 메소드(Newton's method)

뉴턴 메소드는 비선형 방정식의 근을 찾거나 최적화 문제에서 극값을 찾기 위한 반복적인 알고리즘입니다. 이 방법은 뉴턴-랩슨 방법으로도 알려져 있으며, 주로 함수의 근을 찾거나 함수의 최소값 또는 최대값을 계산할 때 사용됩니다.

코드 예시

def f(x):
    return x**2 - 2

def df(x):
    return 2*x

def newton_method(f, df, x0, tolerance=1e-10, max_iter=1000):
    x = x0
    for i in range(max_iter):
        x_new = x - f(x) / df(x)
        if abs(x_new - x) < tolerance:
            return x_new, i+1  # 근과 반복 횟수 반환
        x = x_new
    return x, max_iter

# 초기 추정값 설정
x0 = 1
root, iterations = newton_method(f, df, x0)

print("근:", root)
print("반복 횟수:", iterations)

초기 추정값에 민감: 잘못된 초기 추정값은 수렴을 보장하지 않을 수 있습니다.
함수의 도함수가 필요: f(x)를 알아야 하며, 이 도함수가 0이 되는 지점에서는 사용할 수 없습니다.
반복 횟수와 정밀도 조절: 반복 횟수와 정밀도는 알고리즘의 효율성과 정확성을 결정합니다.

그래디언트 디센트 기반 수치최적화 알고리즘의 기본 아이디어

그래디언트 디센트는 최적화 문제에서 널리 사용되는 알고리즘으로, 함수의 최소값을 찾기 위해 사용됩니다. 이 방법은 주어진 함수의 그래디언트(미분)를 사용하여 각 단계에서 함수의 최소값을 찾아갑니다. 각 반복에서 함수의 현재 위치에서 그래디언트의 반대 방향으로 조금씩 이동하여, 최종적으로 전역 최소값(global minimum) 또는 지역 최소값(local minimum)에 도달하려고 시도합니다.

기본 아이디어

그래디언트 계산: 함수의 현재 지점에서 그래디언트(기울기의 벡터)를 계산합니다.
반대 방향 이동: 그래디언트가 가리키는 방향은 함수가 가장 빠르게 증가하는 방향입니다. 따라서 그래디언트의 반대 방향으로 조금 이동함으로써 함수의 값을 감소시킵니다.
업데이트: 이동 거리는 학습률(learning rate)로 조절합니다. 이 학습률은 이동할 거리를 결정하고, 너무 크거나 작으면 최적화 과정에 부정적인 영향을 줄 수 있습니다.

def f(x):
    return x**2 + 10*x + 25

def df(x):
    return 2*x + 10

def gradient_descent(df, initial_x, learning_rate, tolerance, max_iterations):
    x = initial_x
    for i in range(max_iterations):
        grad = df(x)
        new_x = x - learning_rate * grad
        if abs(new_x - x) < tolerance:
            return new_x, i+1  # 최소값과 반복 횟수 반환
        x = new_x
    return x, max_iterations

# 초기값, 학습률, 정밀도, 최대 반복 횟수 설정
initial_x = 0
learning_rate = 0.1
tolerance = 1e-6
max_iterations = 1000

minimum, iterations = gradient_descent(df, initial_x, learning_rate, tolerance, max_iterations)

print("최소값 위치:", minimum)
print("반복 횟수:", iterations)

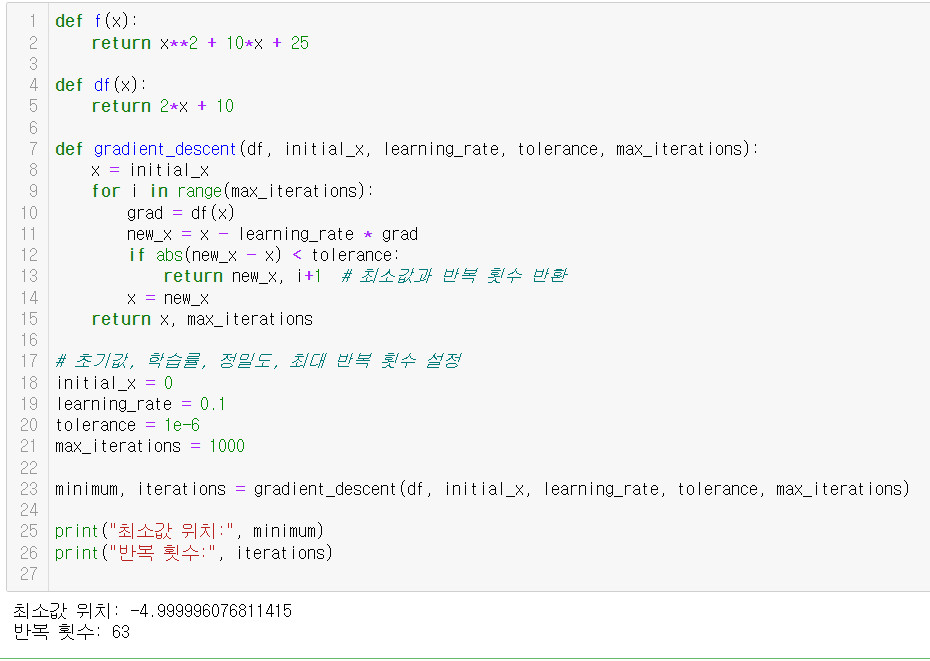
적절한 학습률 선택, 비볼록 함수에서의 지역 최소값 문제, 고차원에서의 효율성 등의 문제를 주의해야 합니다. 이러한 한계점을 가지고 있어서, 아래와 같은 스토캐스틱 방법 - 샘플링을 이용하는 방법이 개발되었습니다.

스토캐스틱 방법

초기값 설정
전체 데이터를 임의로 섞어줌
전체 데이터에서 개수가 m개인 부분집합(미니배치)들을 몇 개 만듦 -> 샘플링
각 부분집합 마다 다음을 적용함
- 순방향 전파를 계산하고 평균 손실함수 값을 계산한다.
- 그래디언트를 계산한다.
- 계산한 그래디언트로 탐색 방향을 설정한다.
- 학습률을 정한다.
- 파라미터 추정치를 업데이트 한다.
만들어진 부분집합을 모두 사용한 후 다시 4번 과정을 Epoch번 반복한다.

확률적 경사 하강법(SGD : Stochastic Gradient Descent)

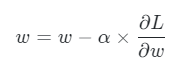
여기서 알파는 학습률을 뜻한다.

모멘텀(Momentum)

모멘텀 최적화는 경사 하강법(Gradient Descent)의 한 변형으로, 이전 단계의 업데이트를 참고하여 가중치를 업데이트하는 방법입니다. 이는 물리학에서의 관성의 원리와 유사하게, 이전 그래디언트가 현재 그래디언트에 영향을 미치면서, 골짜기를 더 빠르게 내려가거나 최적점에 더 안정적으로 도달하게 합니다.

과거 그래디언트의 평균을 이용해 현재 그래디언트를 업데이트하는 방식으로, 이를 통해 최적화 과정이 보다 안정적이고 빠르게 수렴합니다. 모멘텀은 과거의 업데이트를 '관성'으로써 이해할 수 있으며, 이 관성이 모델을 국소 최소값(local minima)이나 고원(saddle points)에서 벗어나게 도와줍니다.

import numpy as np

def f(x):
    return x**2 + 10*x + 25

def df(x):
    return 2*x + 10

def momentum(df, initial_x, learning_rate=0.01, gamma=0.9, max_iterations=1000):
    v = 0
    x = initial_x
    for i in range(max_iterations):
        g = df(x)
        v = gamma * v - learning_rate * g
        x += v
        if abs(df(x)) < 1e-5:
            break
    return x

initial_x = 0
minimum = momentum(df, initial_x)

print("최소값 위치:", minimum)

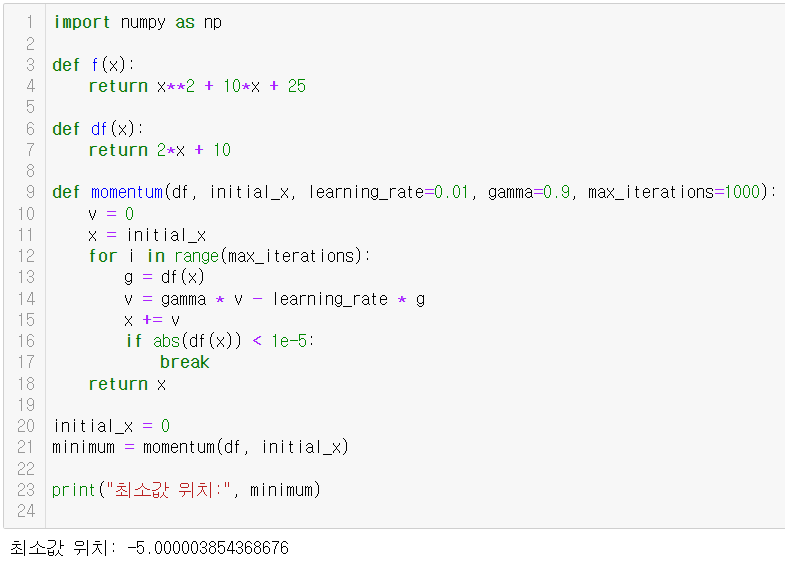
AdaGrad

AdaGrad(Adaptive Gradient Algorithm)는 학습률을 각 매개변수에 대해 개별적으로 조정하여 수행합니다. 많이 변경된 매개변수의 학습률을 낮추고, 적게 변경된 매개변수의 학습률을 높입니다.

import numpy as np

def f(x):
    return x**2 + 10*x + 25

def df(x):
    return 2*x + 10

def adagrad(df, initial_x, learning_rate=0.01, epsilon=1e-8, max_iterations=1000):
    g_squared = 0
    x = initial_x
    for i in range(max_iterations):
        g = df(x)
        g_squared += g**2
        x -= learning_rate / np.sqrt(g_squared + epsilon) * g
        if abs(df(x)) < 1e-5:
            break
    return x

initial_x = 0
minimum = adagrad(df, initial_x)

print("최소값 위치:", minimum)

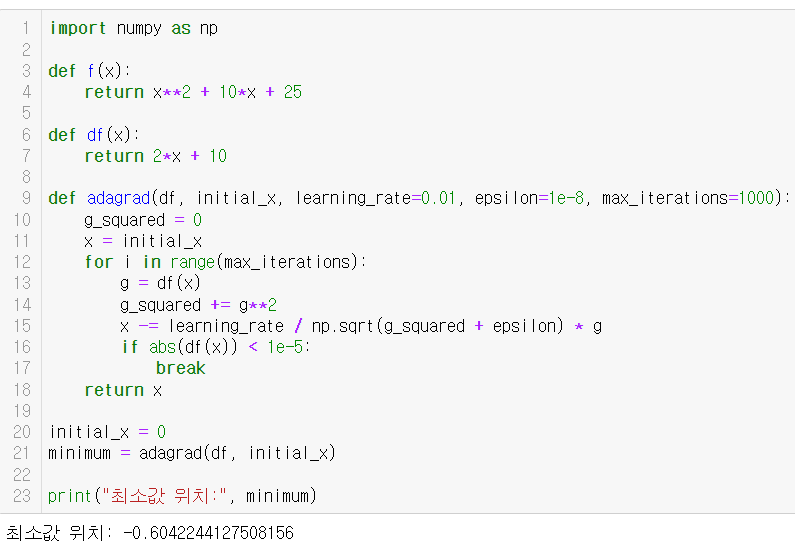
RMSprop

RMSprop은 AdaGrad의 확장으로, 학습률이 너무 빠르게 감소하는 문제를 해결하기 위해 과거의 모든 그래디언트를 고르게 누적하지 않고 최근의 그래디언트를 더 많이 반영합니다.

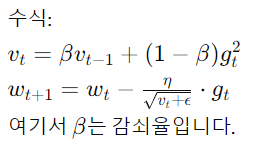
import numpy as np

def f(x):
    return x**2 + 10*x + 25

def df(x):
    return 2*x + 10

def adam(df, initial_x, learning_rate=0.1, beta1=0.9, beta2=0.999, epsilon=1e-8, max_iterations=1000):
    m, v = 0, 0
    x = initial_x
    for t in range(1, max_iterations + 1):
        g = df(x)
        m = beta1 * m + (1 - beta1) * g
        v = beta2 * v + (1 - beta2) * (g**2)
        m_hat = m / (1 - beta1**t)
        v_hat = v / (1 - beta2**t)
        x -= learning_rate * m_hat / (np.sqrt(v_hat) + epsilon)
        if abs(df(x)) < 1e-5:
            break
    return x

# 초기값 설정
initial_x = 0
minimum = adam(df, initial_x)

print("최소값 위치:", minimum)

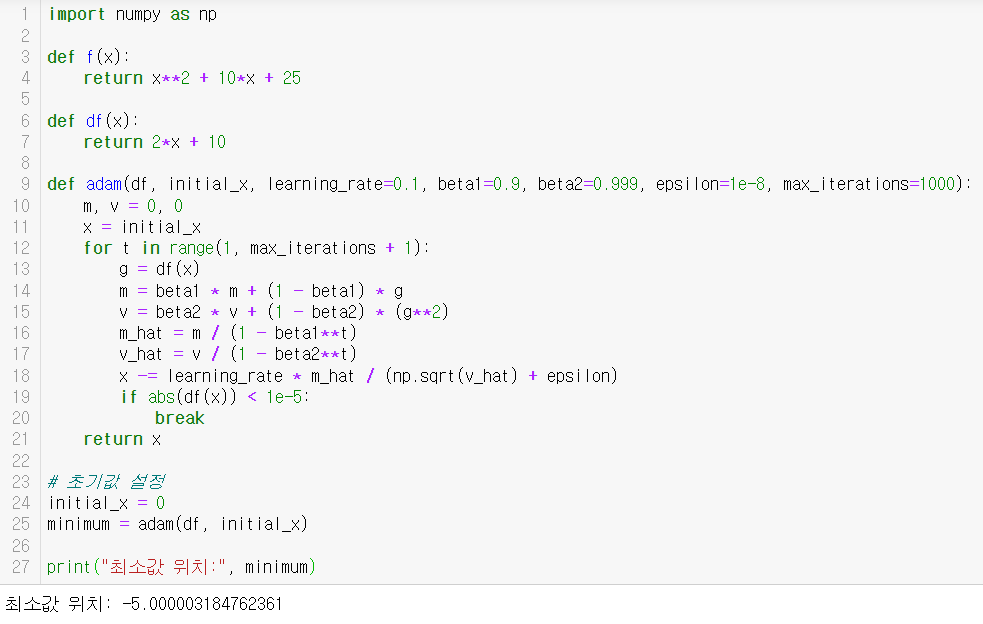
Adam

Adam(Adaptive Moment Estimation)은 RMSprop과 모멘텀 최적화를 결합한 알고리즘으로, 그래디언트의 1차 모멘트(평균)와 2차 모멘트(비평방)를 모두 계산합니다.

# 간단한 2차 함수 최적화 (Adam)
import numpy as np

def f(x):
    return x**2 + 10*x + 25

def df(x):
    return 2*x + 10

def adam(df, initial_x, learning_rate=0.1, beta1=0.9, beta2=0.999, epsilon=1e-8, max_iterations=1000):
    m, v = 0, 0
    x = initial_x
    for t in range(1, max_iterations + 1):
        g = df(x)
        m = beta1 * m + (1 - beta1) * g
        v = beta2 * v + (1 - beta2) * (g**2)
        m_hat = m / (1 - beta1**t)
        v_hat = v / (1 - beta2**t)
        x -= learning_rate * m_hat / (np.sqrt(v_hat) + epsilon)
        if abs(df(x)) < 1e-5:
            break
    return x

# 초기값 설정
initial_x = 0
minimum = adam(df, initial_x)

print("최소값 위치:", minimum)