연속 합 문제를 Swift로 풀어보자

이 문제를 1차원 적으로 접근해보자.
for 문을 두번 돌려서 문제를 푼다고 생각 할 것이다.
예제 ( 10, -4, 3, 1, 5, 6, -35, 12, 21, -1 ) 을 예로 들면,
10 부터 -1 까지 돌려가며 최댓값을 저장하고,
-4 부터 -1 까지 돌리며 최댓값을 저장하고,
3 부터 -1, 1부터 -1 .... 그렇게 n * (n + 1) / 2 만큼 배열을 돌리며 최댓값을 구할 것이다.
dp를 사용해보자
한번만 for문을 돌려서 풀 수 있는 방법을 고민해보자.
먼저 for 문을 돌리기 전 , 모든 숫자가 음수라면, 즉 원소 중 최댓값이 음수라면 정답은 음수가 될 것이다.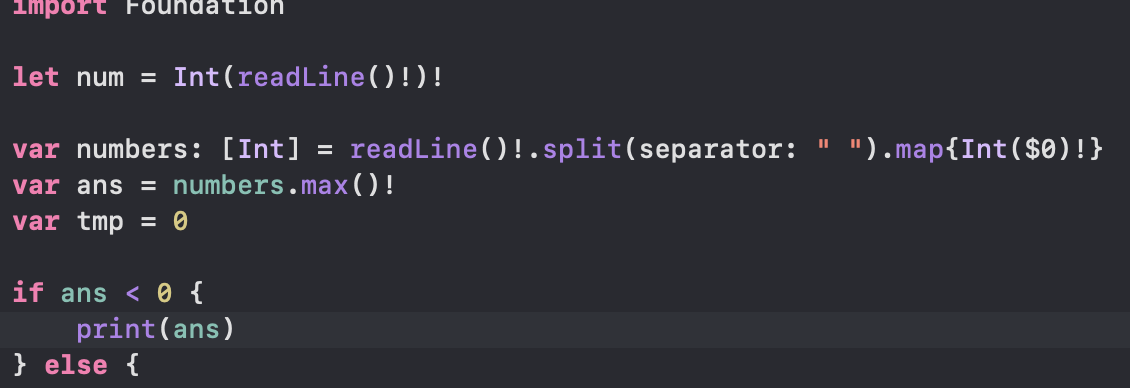
ans = numbers.max()! , 그리고 ans < 0 이면 print(ans) 로 솔루션을 종료한다.
이러한 특수상황이 아닐 때를 고민해보자.
1
- 10
- tmp = 10
- ans = 21
먼저 10 이 나온다.
10은 양수이다. 현재 ans 에는 21 ( numbers.max()!) 이 저장되어있다.
tmp 에 10 을 더해준다
2
- 10 -4
- tmp = 6
- ans = 21
다음에 -4 가 나온다.
-4는 음수이다. 따라서
-4 부터 시작하는 연속 된 수들의 합은, 10부터 시작하는 연속된 수들의 합보다 클 수가 없다.
따라서 tmp 에는 -4, 10 -4 =6 중 더 큰 수인 6이 들어간다.
3
- 10 -4 3
- tmp = 9
- ans = 21
다음은 3이 나온다.
10 -4 + 3 , -4 + 3 , 3 중 가장 큰 9 가 tmp 에 들어간다. 아직 ans 이 tmp 보다 크다.
여기까지 했으면 감이 잡힌다.
어찌되었던 numbers[0] 부터 numbers[i] 까지의 합이 numbers[i] 보다 크다면,
앞으로도 연속된 수의 합은 전자가 더크다.
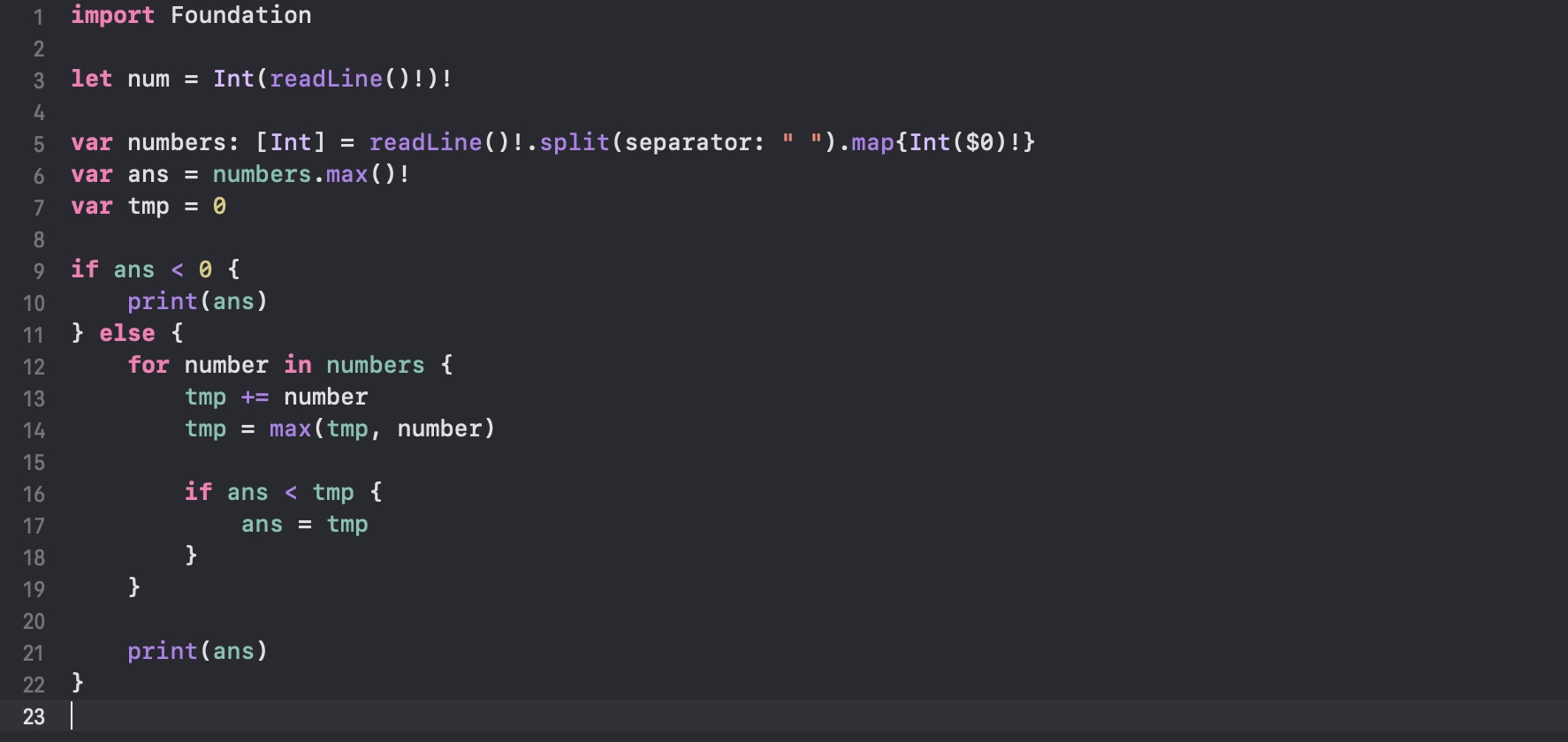
코드