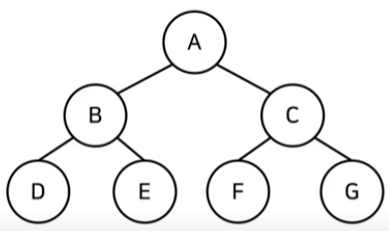
트리란

트리(Tree)는 계층적인 구조를 가지며, 여러 개의 노드가 간선으로 연결되어 있는 자료구조입니다. 트리는 하나의 루트(Root) 노드에서 시작하여 여러 개의 자식 노드를 가질 수 있습니다. 각 노드는 부모-자식 관계로 연결되어 있으며, 각 자식 노드는 그 자체로 서브 트리(Subtree)를 형성할 수 있습니다.

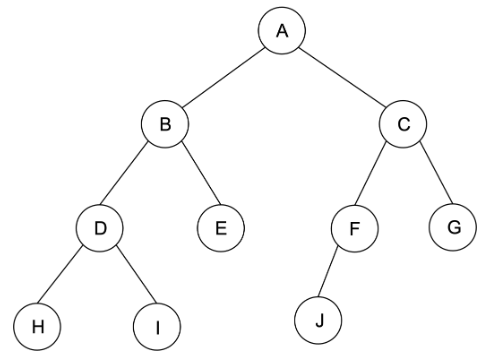
트리의 주요 용어

루트(Root): 트리의 시작 노드로, 다른 모든 노드는 이 루트에서부터 시작하는 서브 트리의 일부입니다.

노드(Node): 트리의 각 원소로, 데이터를 저장하고 다른 노드와 연결된 간선(Edge)을 가집니다.

잎 노드(Leaf Node): 자식이 없는 노드를 의미하며, 가장 끝단에 위치한 노드입니다.

부모(Parent): 어떤 노드의 바로 위에 있는 노드를 가리킵니다.

자식(Child): 어떤 노드 아래에 연결된 노드를 가리킵니다.

형제(Sibling): 같은 부모를 가진 노드들을 가리킵니다.

높이(Height): 트리의 가장 깊은 깊이를 나타냅니다

이진 트리(binary tree)

자식 노드의 갯수가 최대 2개로 한정된 tree를 말합니다.

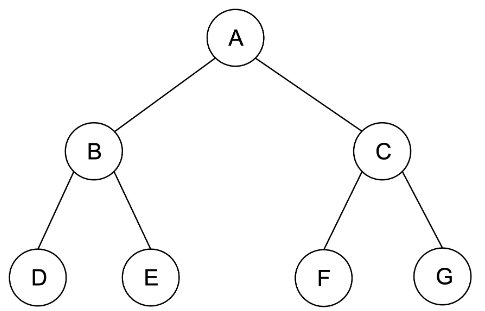
최대 자식 노드 갯수가 2개인것 뿐이므로 위 그림에서 G 노드가 없어도 이진 트리입니다.

이진 탐색 트리(binary search tree)

이진 탐색이 동작할 수 있도록 고안된 자료구조의 일종입니다.

왼쪽 자식 노드가 부모 노드보다 작고

오른쪽 자식 노드가 부모 노드보다 큰 이진 트리를 말합니다.

왼쪽 자식 < 부모 < 오른쪽 자식

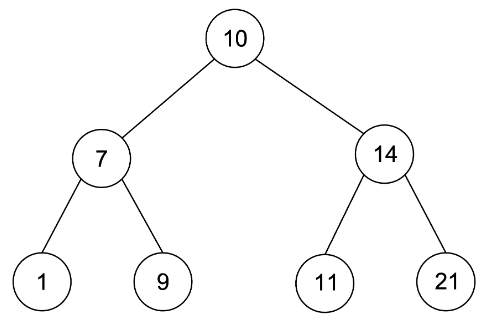
위와 같은 조건이 성립하면 원하는 값을 찾고 싶을 때 해당 값을 Root node의 값과 비교하여 왼쪽 혹은 오른쪽으로 탐색 해 나갈 수 있습니다.

4. 트리 순회(Tree Travercal)

트리 자료구조에 포함된 노드를 특정한 방법으로 한 번씩 방문하는 방법을 의미합니다.

보통 자신을 출력하는 방법과 같이 방문한 노드를 시각적으로 확인 가능합니다.

In order / 중위 순회 ( Left - Root - Right )

왼쪽 노드부터 출력합니다.

이후 Root 노드를 출력합니다.

이후 오른쪽 노드를 출력합니다.

(예제를 중위 순회 하면 D-B-E-A-F-C-G 입니다.)

pre order / 전위 순회 ( Root - Left - Right )

Root 노드를 먼저 출력합니다.

이후 왼쪽 오른쪽 순으로 출력합니다.

(예제를 전위 순회 하면 A-B-D-E-C-F-G 입니다.)

post order / 후위 순회 ( Left - Right - Root )

왼쪽 노드부터 출력합니다.

이후 오른쪽 노드를 출력합니다.

이후 Root 노드를 출력합니다.

(예제를 후위 순회 하면 D-E-B-F-G-C-A 입니다.)