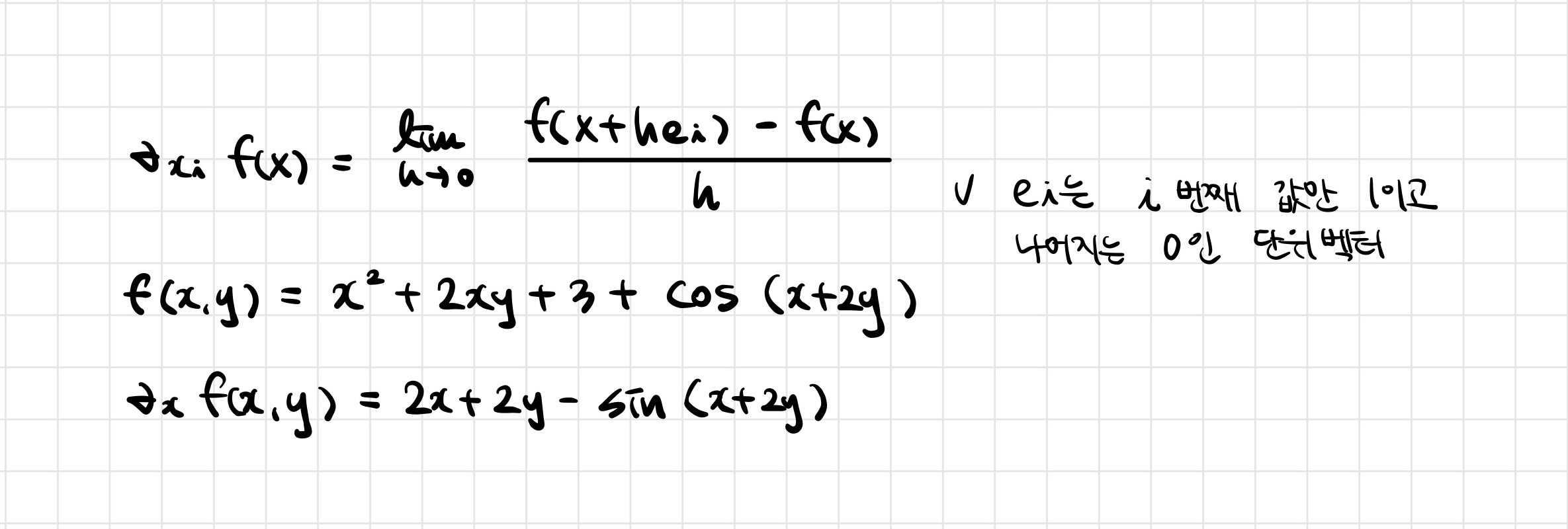[부스트캠프 AI Tech 5기] Pre-Course : (16) 경사하강법 (순한맛)

📖 미분이 뭔가요?

• 미분(differentiation)은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로 최적화에서 제일 많이 사용하는 기법
• 최근엔 미분을 손으로 직접 계산하는 대신 컴퓨터가 계산해줄 수 있음

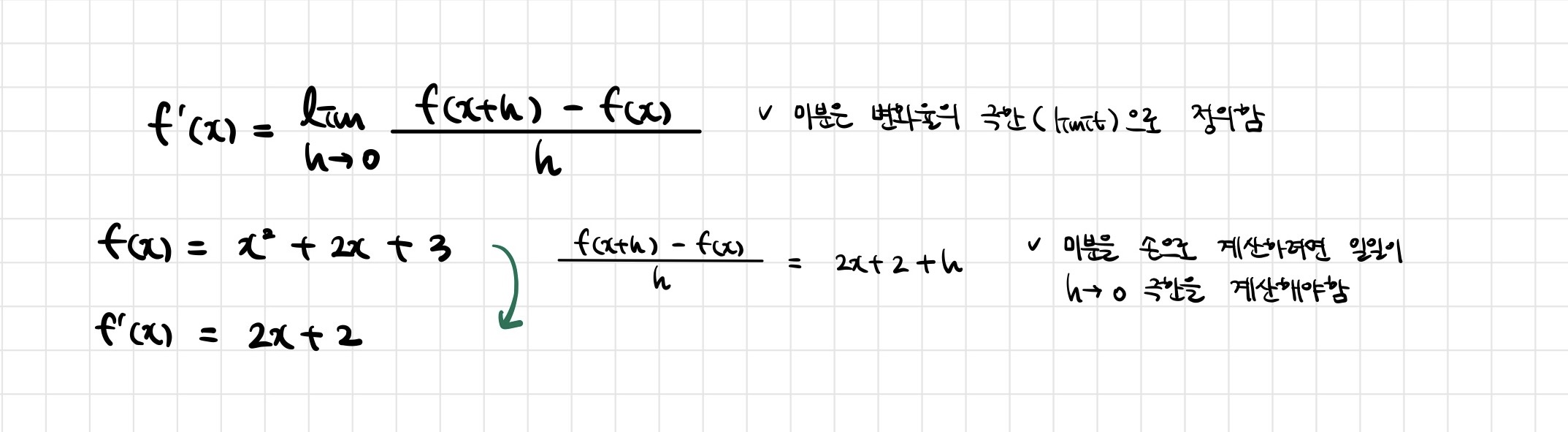
import sympy as sym
from sympy.abc import x

sym.diff(sym.poly(x**2 + 2*x + 3), x)

Poly(2𝑥+2,𝑥,𝑑𝑜𝑚𝑎𝑖𝑛=ℤ)

📖 미분을 그림으로 이해해보자

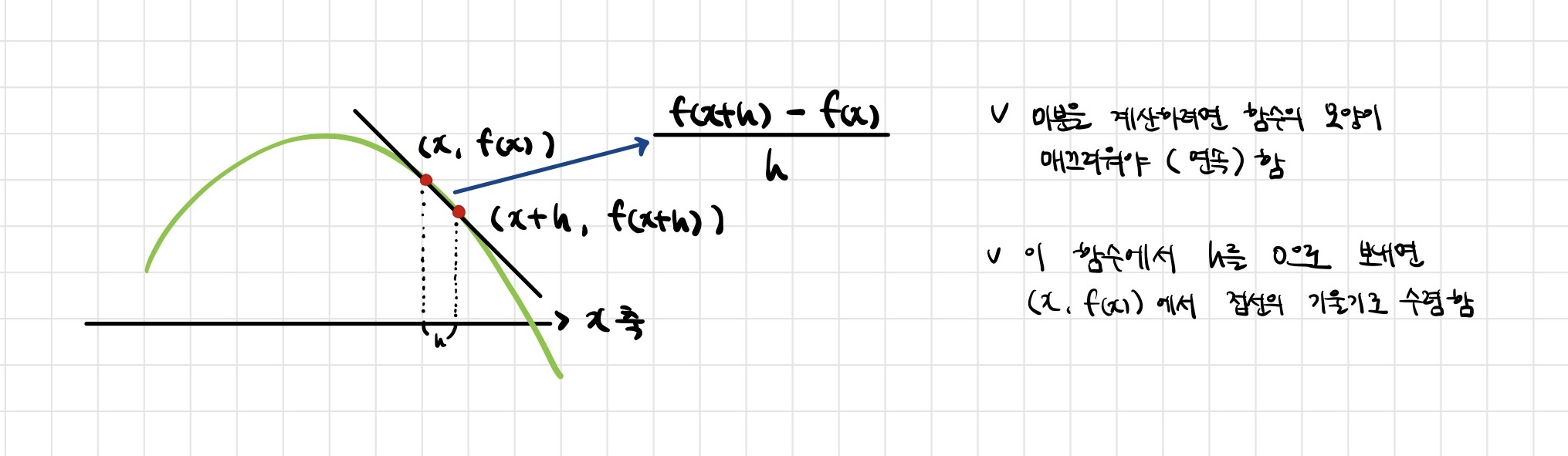
• 미분이란 함수 f의 주어진 점 (x,f(x))에서의 접선의 기울기를 구하는 것
• 한 점에서 접선의 기울기를 알면 어느 방향으로 점을 움직여야 함수값이 증가하는지/감소하는지 알 수 있음

📖 미분을 어디에 쓸까?

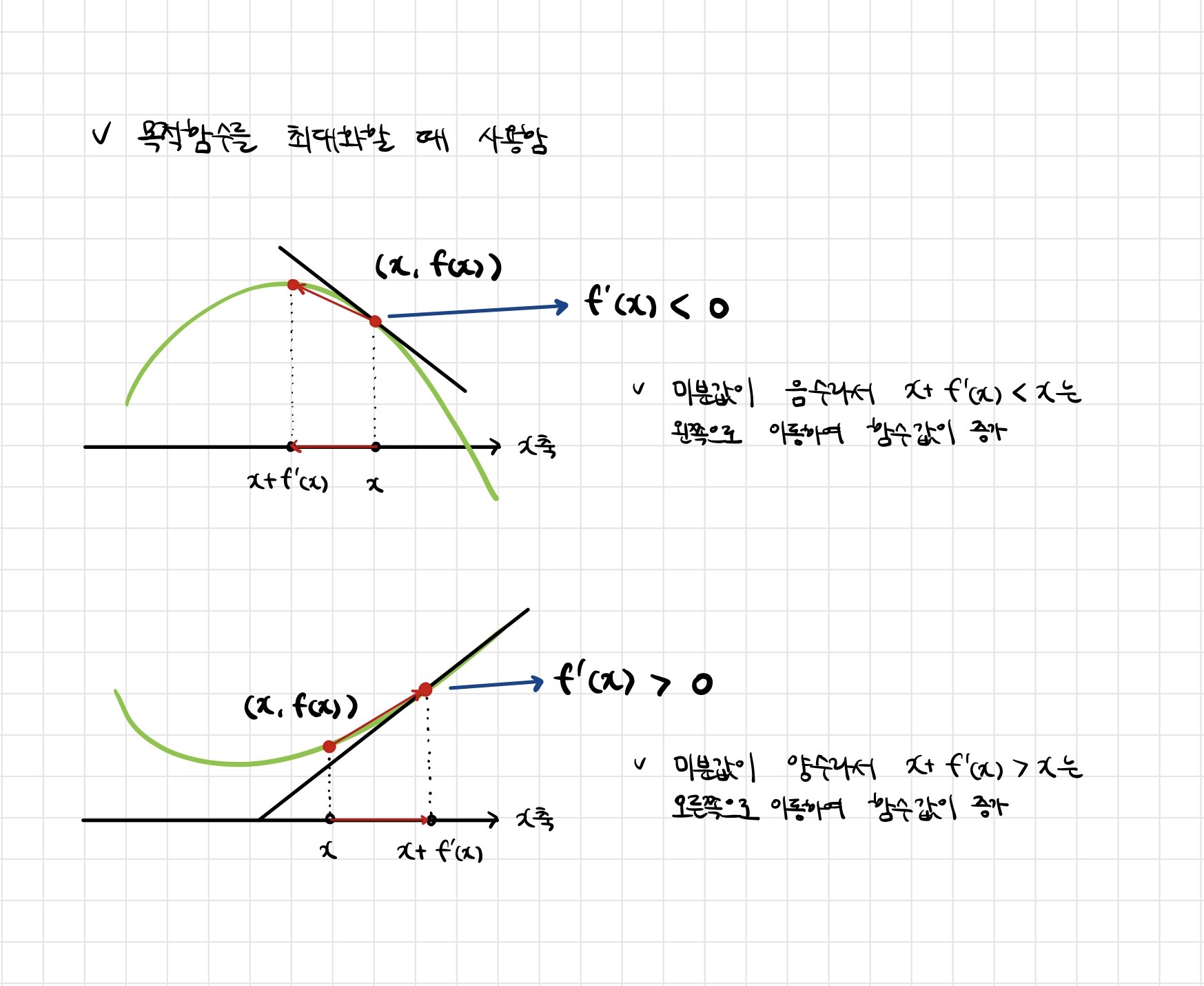
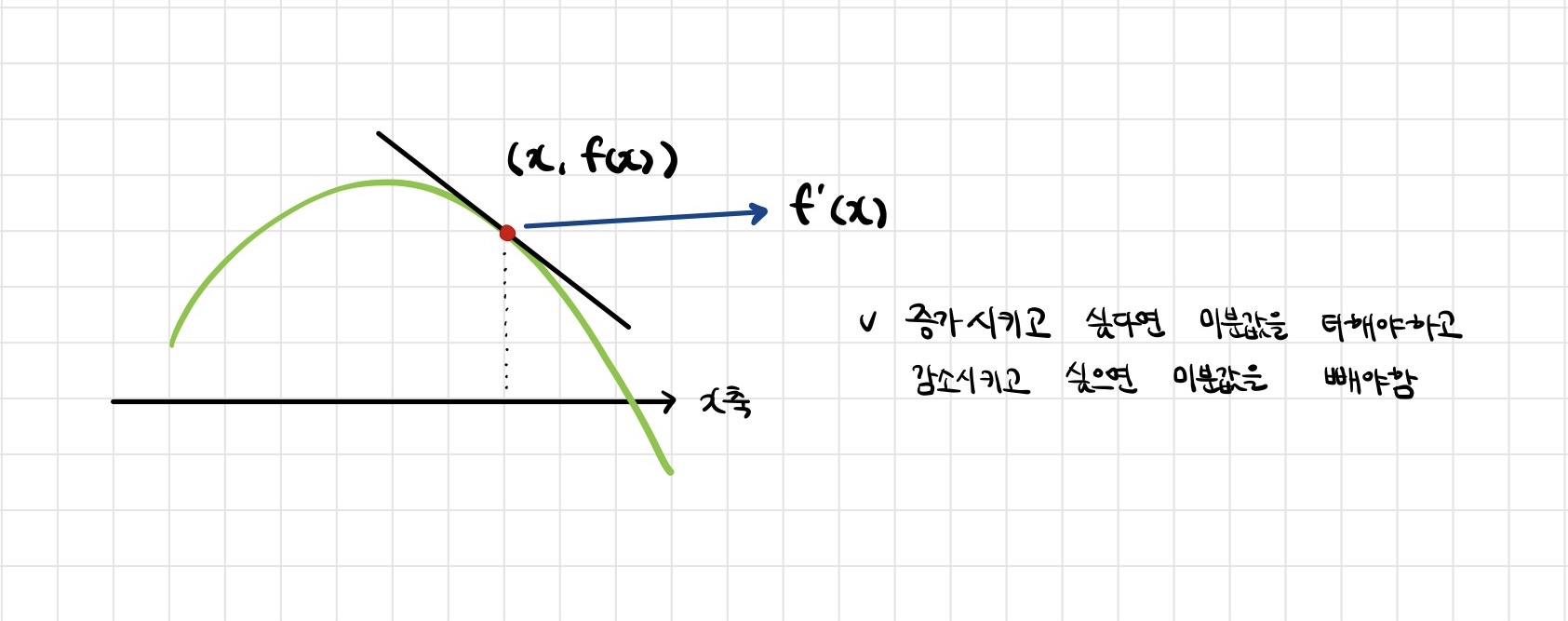
• 미분값을 더하면 경사상승법(gradient ascent)이라 하며 함수의 극대값의 위치를 구할 때 사용함
  

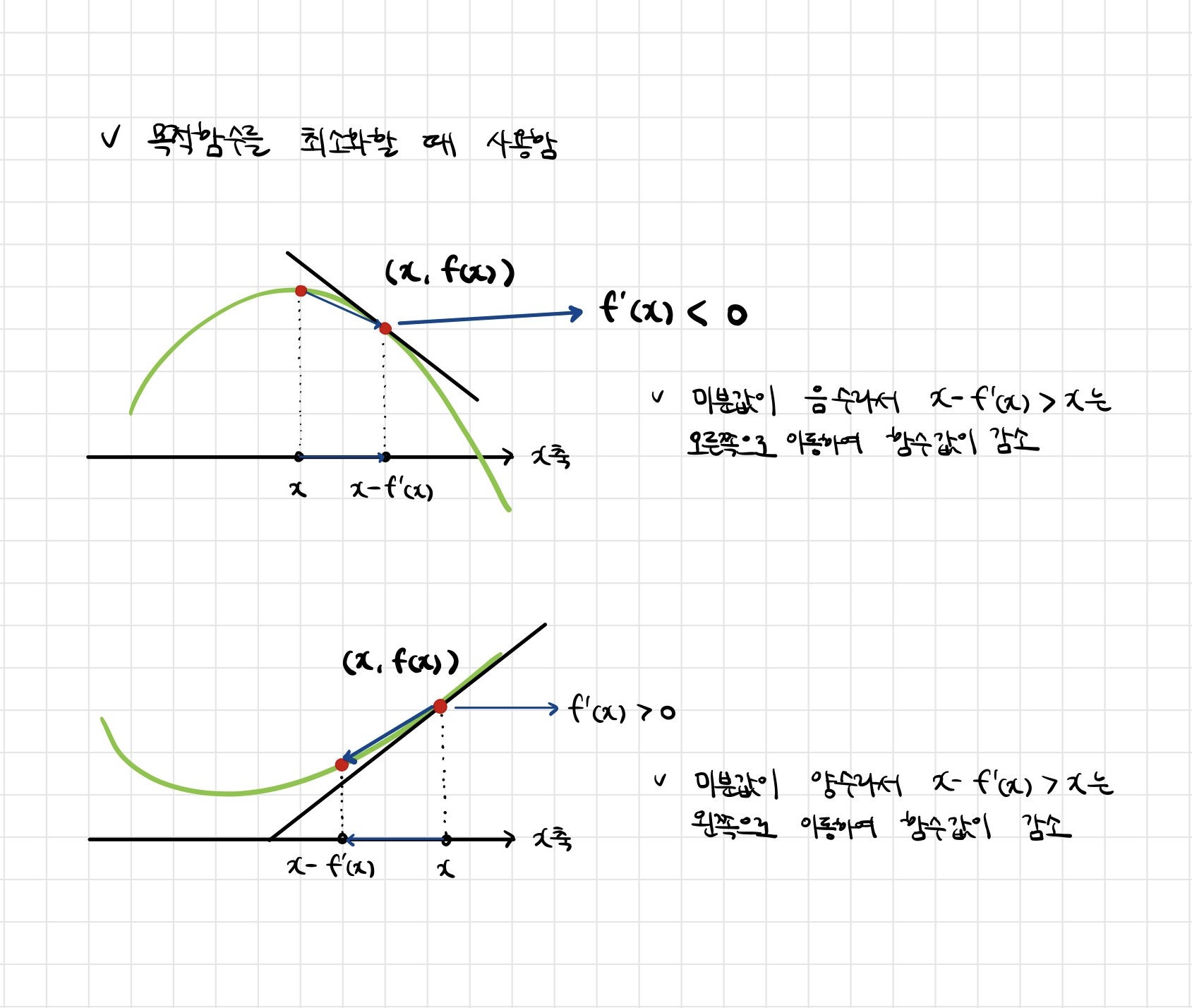
• 미분값을 빼면 경사하강법(gradient descent)이라 하며 함수의 극소값의 위치를 구할 때 사용함
  

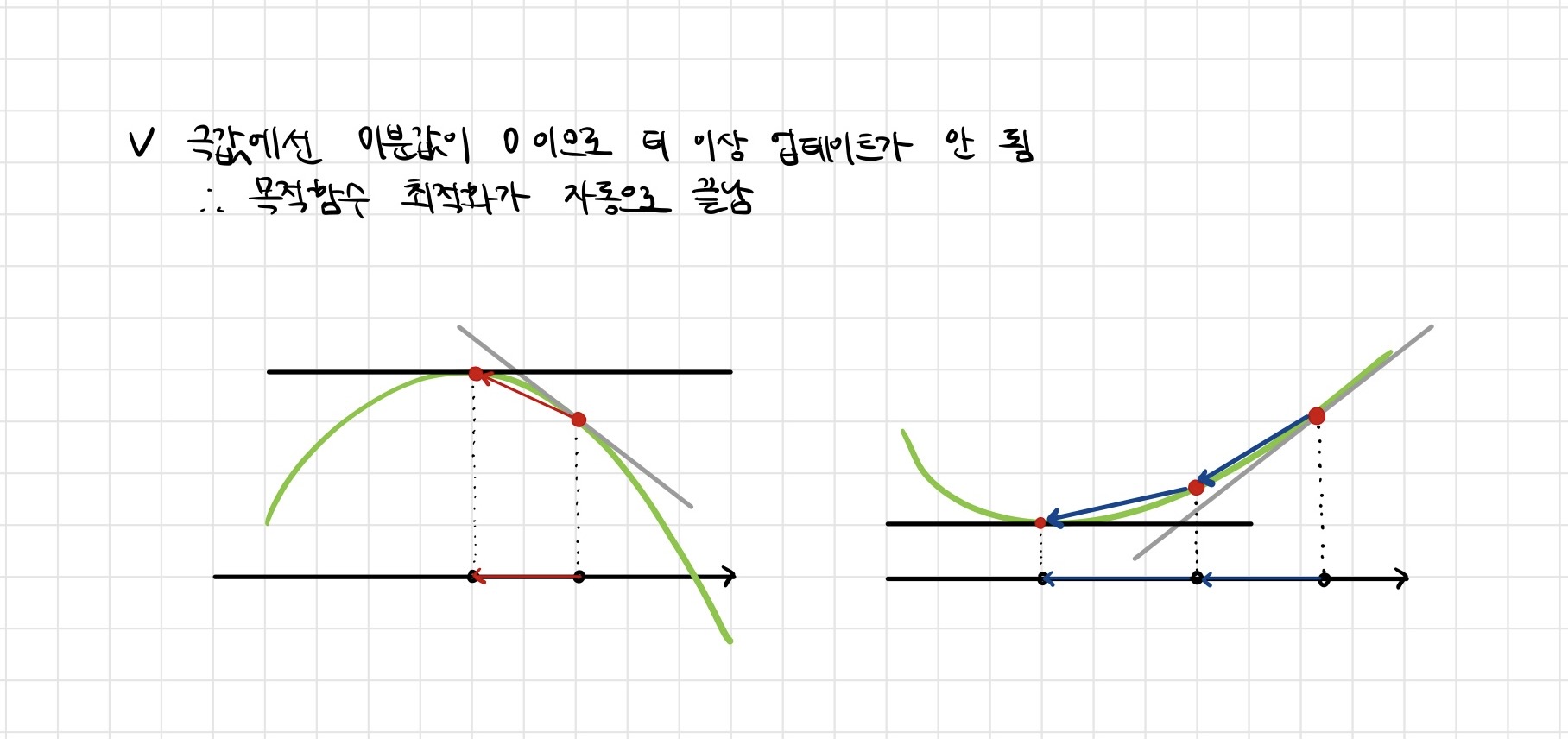
• 경사상승/경사하강 방법은 극값에 도달하면 움직임을 멈춤
  

📖 경사하강법 : 알고리즘

Input : gradient, init, lr, eps, Output: var
# gradient : 미분을 계산하는 함수
# init : 시작점, lr : 학습률, eps : 알고리즘 종료조건

var = init
grad = gradient(var)
while (abs(grad) > eps):
	var = var - lr * grad
    grad = gradient(var)

• 컴퓨터로 계산할 때 미분이 정확히 0이 되는 것은 불가능하므로 eps 보다 작을 때 종료하는 조건이 필요함
• var = var - lr * grad : 이 부분이 x - λf'(x)을 게산하는 부분으로, lr은 학습률로써 미분을 통해 업데이트하는 속도를 조절함
• grad = gradient(var) : 종료조건이 성립하기 전까지 미분값을 계속 업데이트함

import sympy as sym
from sympy.abc import x
import numpy as np

def func(val):
    fun = sym.poly(x**2 + 2*x + 3)
    return fun.subs(x, val), fun

def func_gradient(fun, val):
    _, function = fun(val)
    diff = sym.diff(function, x)
    return diff.subs(x, val), diff

def gradient_descent(fun, init_point, lr_rate = 1e-2, epsilon = 1e-5):
    cnt = 0
    val = init_point
    diff, _ = func_gradient(fun, init_point)
    while np.abs(diff) > epsilon:
        val = val - lr_rate * diff
        diff, _ = func_gradient(fun, val)
        cnt += 1
    
    print("함수: {}, 연산횟수: {}, 최소점: ({}, {})".format(fun(val)[1], cnt, val, fun(val)[0]))
    
gradient_descent(fun = func, init_point = np.random.uniform(-2,2))

함수: Poly(x**2 + 2*x + 3, x, domain='ZZ'), 연산횟수: 630, 최소점: (-0.999995034961538, 2.00000000002465)

📖 변수가 벡터이면요?

• 벡터가 입력인 다변수 함수의 경우 편미분(partial differentiation)을 사용함

import sympy as sym
from sympy.abc import x

sym.diff(sym.poly(x**2 + 2*x*y + 3) + sym.cos(x + 2*y), x)

• 각 변수 별로 편미분을 계산한 그레디언트(gradient) 벡터를 이용하여 경사하강/경사상승법에 사용할 수 있음

📖 그레디언트 벡터가 뭐에요?

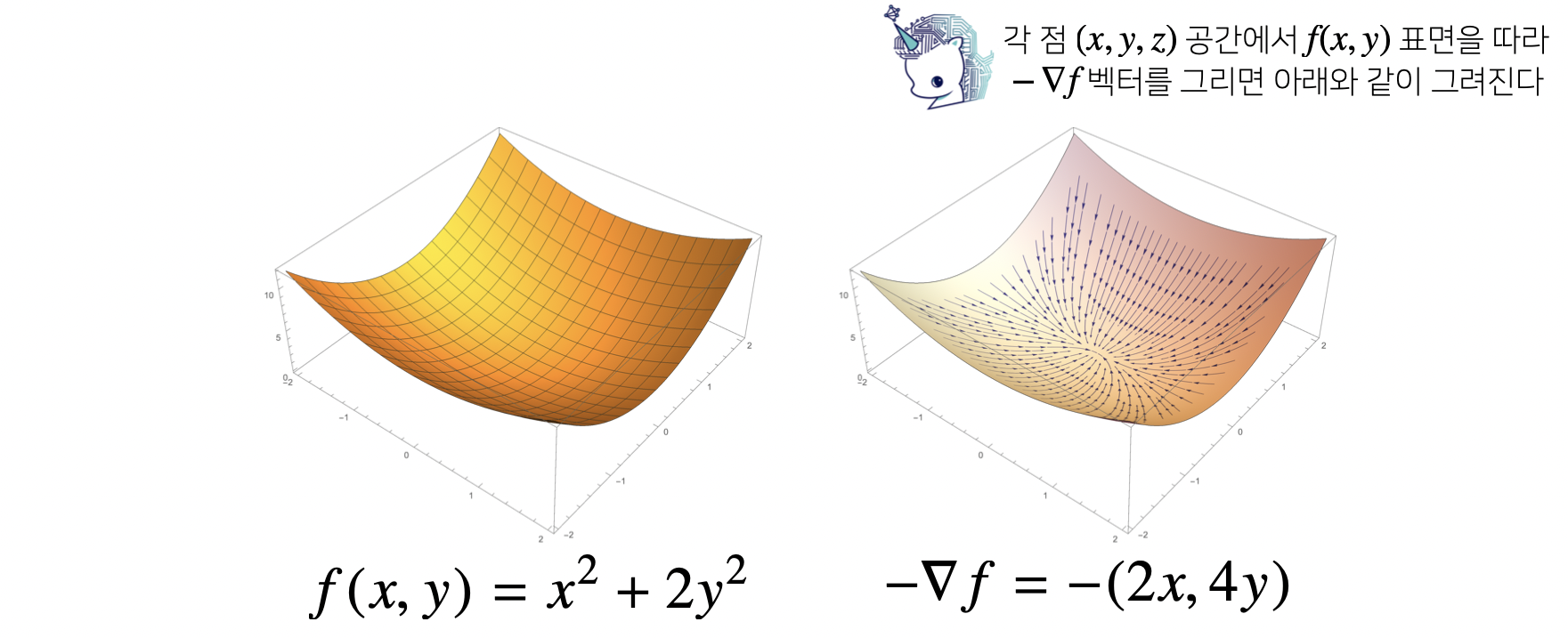
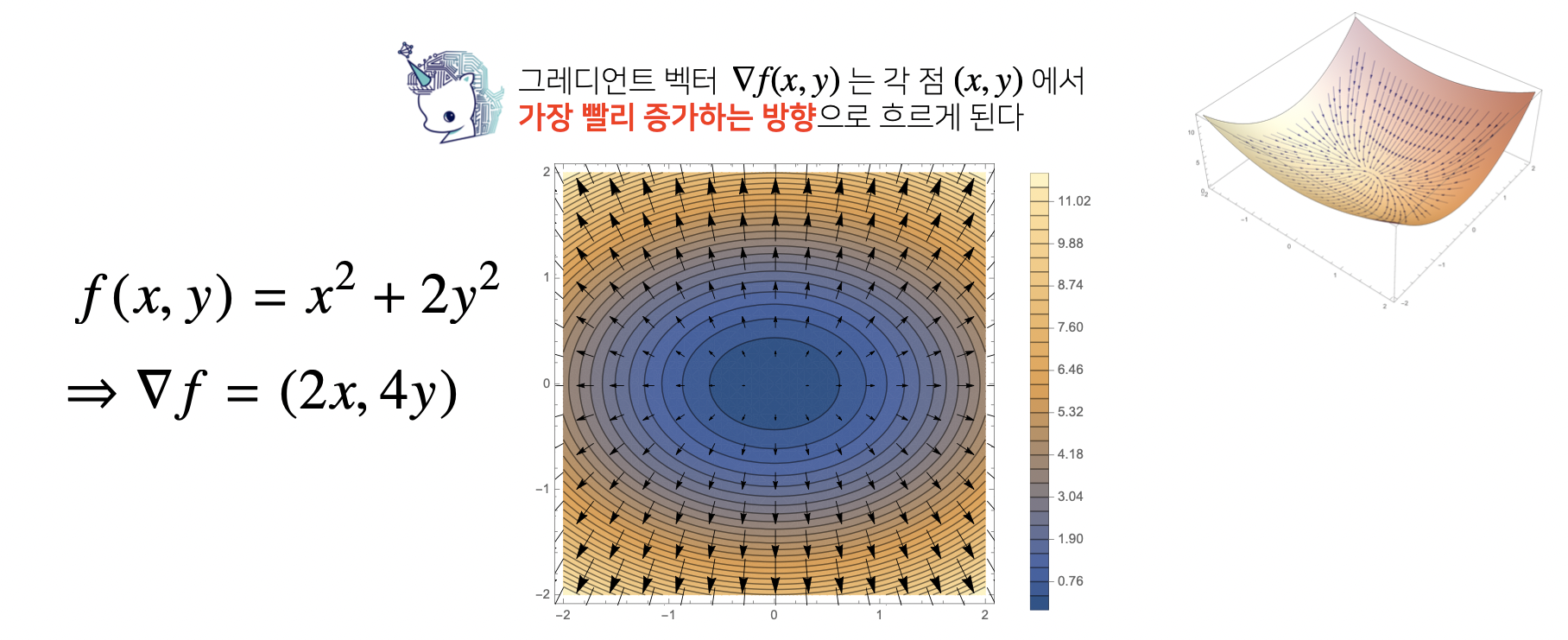
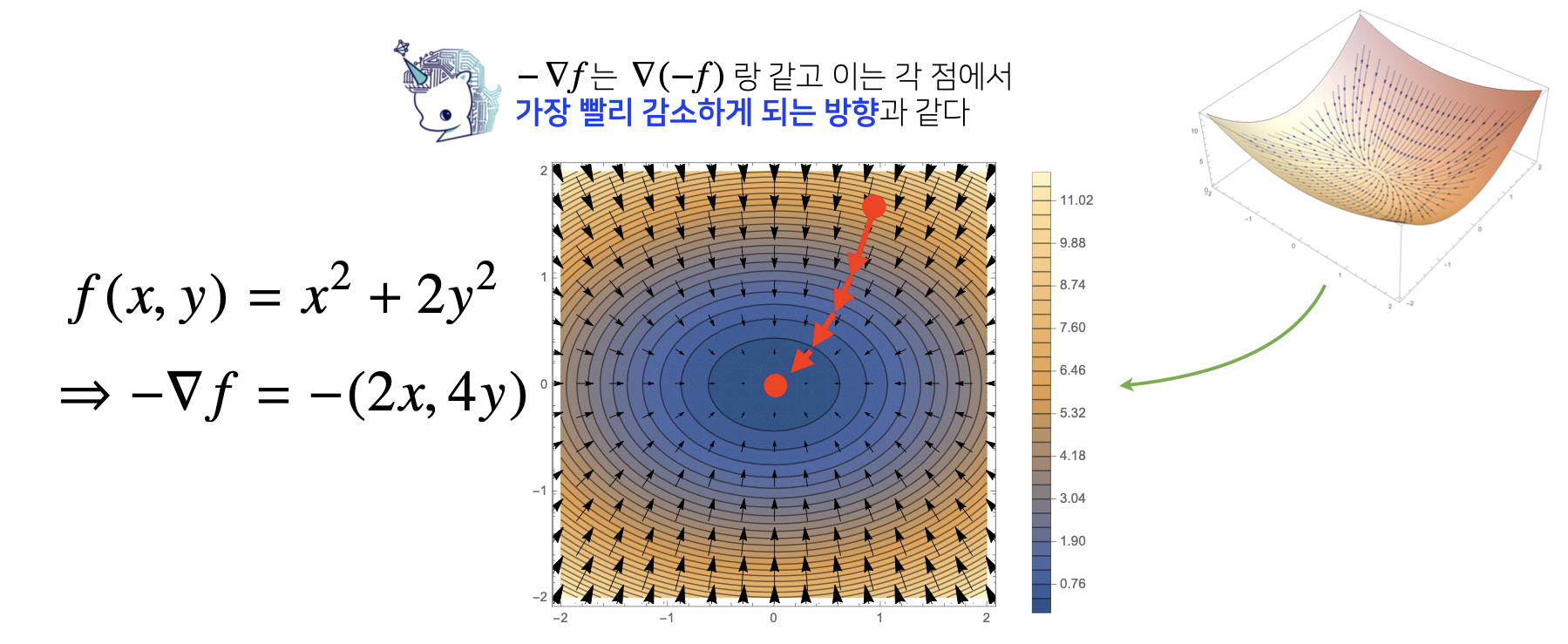
📖 경사하강법 : 알고리즘 (그레디언트 벡터 ver.)

Input : gradient, init, lr, eps, Output: var
# gradient : 그레디언트 벡터를 계산하는 함수
# init : 시작점, lr : 학습률, eps : 알고리즘 종료조건

var = init
grad = gradient(var)
while (norm(grad) > eps):
	var = var - lr * grad
    grad = gradient(var)

• 경사하강법 알고리즘은 그대로 적용됨
• 그러나 벡터에서는 절대값 대신 노름(norm)을 계산해서 종료조건을 설정

# 함수가 f(x) = x**2 + 2*y**2 일 때 경사하강법으로 최소점을 찾는 코드
# Multivariate Gradient Descent

import sympy as sym
from sympy.abc import x
import numpy as np

def eval_(fun, val):
    val_x, val_y = val
    fun_eval = fun.subs(x, val_x).subs(y, val_y)
    return fun_eval

def func_multi(val):
    x_, y_ = val
    func = sym.poly(x**2 + 2*y**2, x, y)
    return eval_(func, [x_, y_]), func

def func_gradient(fun, val):
    x_, y_ = val
    _, function = fun(val)
    diff_x = sym.diff(function, x)
    diff_y = sym.diff(function, y)
    grad_vec = np.array([eval_(diff_x,[x_,y_]), eval_(diff_y,[x_,y_])], dtype=float)
    return grad_vec, [diff_x, diff_y]

def gradient_descent(fun, init_point, lr_rate = 1e-2, epsilon = 1e-5):
    cnt = 0
    val = init_point
    diff, _ = func_gradient(fun, val)
    while np.norm(diff) > epsilon:
        val = val - lr_rate * diff
        diff, _ = func_gradient(fun, val)
        cnt += 1
    
    print("함수: {}, 연산횟수: {}, 최소점: ({}, {})".format(fun(val)[1], cnt, val, fun(val)[0]))

pt = [np.random.uniform(-2,2),np.random.uniform(-2,2)]
gradient_descent(fun = func, init_point = pt)

# 이유는 알 수 없지만 해당 코드를 입력하면 name 'y' is not defined 라는 오류가 뜸
# 우선 강의 자료에 나와있는 출력값은 다음과 같음
함수: Poly(x**2 + 2*y**2, x, y, domain='zz'), 연산횟수: 606, 최소점: ([4.95901570e-06 2.88641061e-11], 2.45918366929856E-11)

<이 게시물은 임성빈 교수님의 '경사하강법 (순한맛)' 강의 자료를 참고하여 작성되었습니다.>

본 포스트의 학습 내용은 [부스트캠프 AI Tech 5기] Pre-Course 강의 내용을 바탕으로 작성되었습니다.
부스트캠프 AI Tech 5기 Pre-Course는 일정 기간 동안에만 운영되는 강의이며,
AI 관련 강의를 학습하고자 하시는 분들은 부스트코스 AI 강좌에서 기간 제한 없이 학습하실 수 있습니다.
(https://www.boostcourse.org/)