[부스트캠프 AI Tech 5기] Pre-Course : (19) 선형 변환

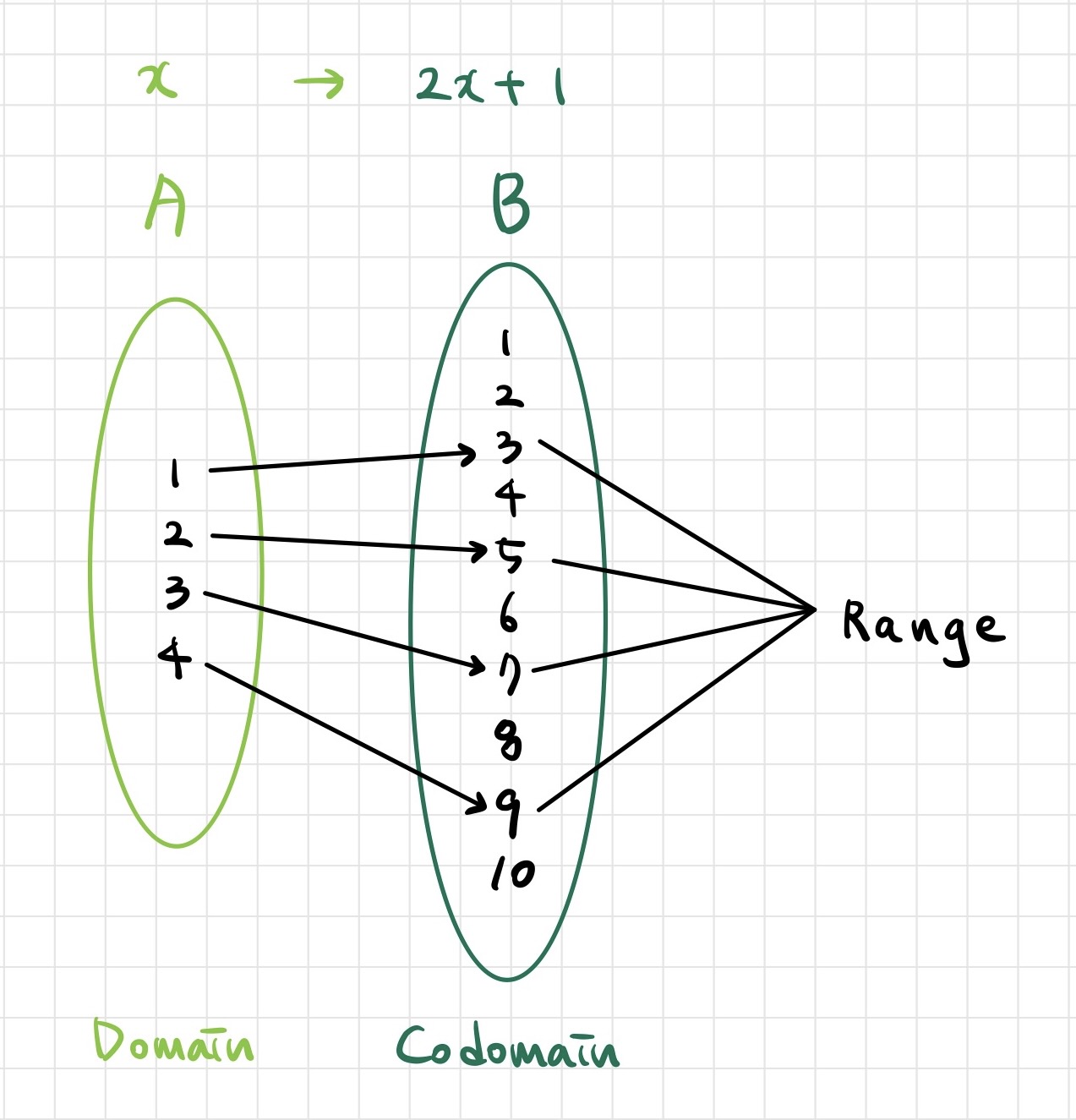
📖 Transformation

• A transformation, function, or mapping, $𝑇$
  maps an input 𝑥 to an output 𝑦
  • Mathematical notation: $𝑇: 𝑥 ↦ 𝑦$
• Domain: Set of all the possible values of 𝑥
• Co-domain: Set of all the possible values of 𝑦
• Image: a mapped output 𝑦, given 𝑥
• Range: Set of all the output values mapped by each 𝑥 in the domain
• Note: the output mapped by a particular 𝑥 is uniquely determined.

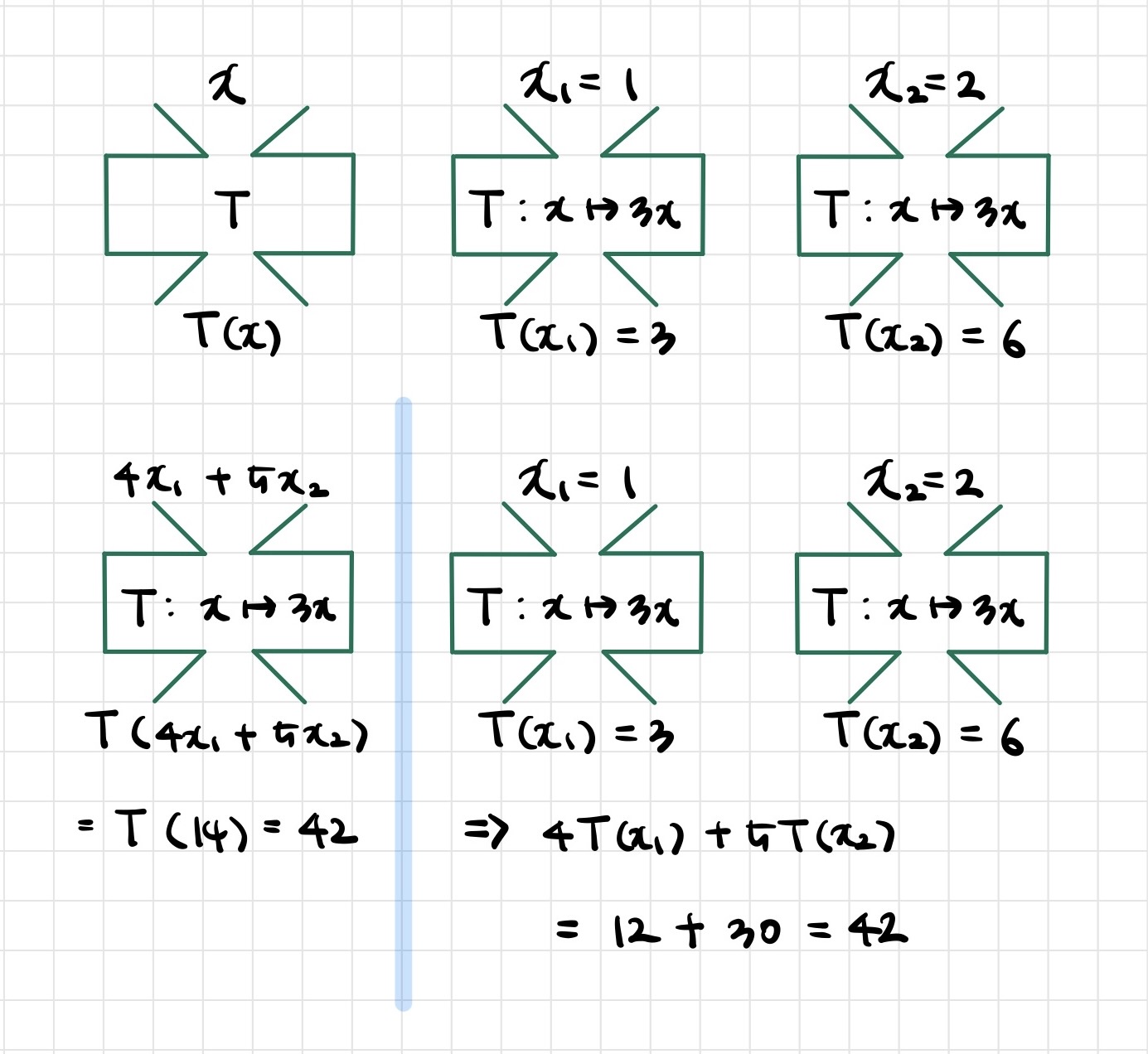
📖 Linear Transformation

• Definition: A transformation (or mapping) 𝑇 is linear if:
  I. $𝑇(𝑐𝐮 + 𝑑𝐯) = 𝑐 𝑇(𝐮) + 𝑑 𝑇(𝐯)$ for all $𝐮, 𝐯$ in the domain of 𝑇 and and for all scalars 𝑐 and 𝑑
• Simple example: $𝑇: 𝑥↦𝑦, 𝑇(𝑥) =𝑦 =3𝑥$

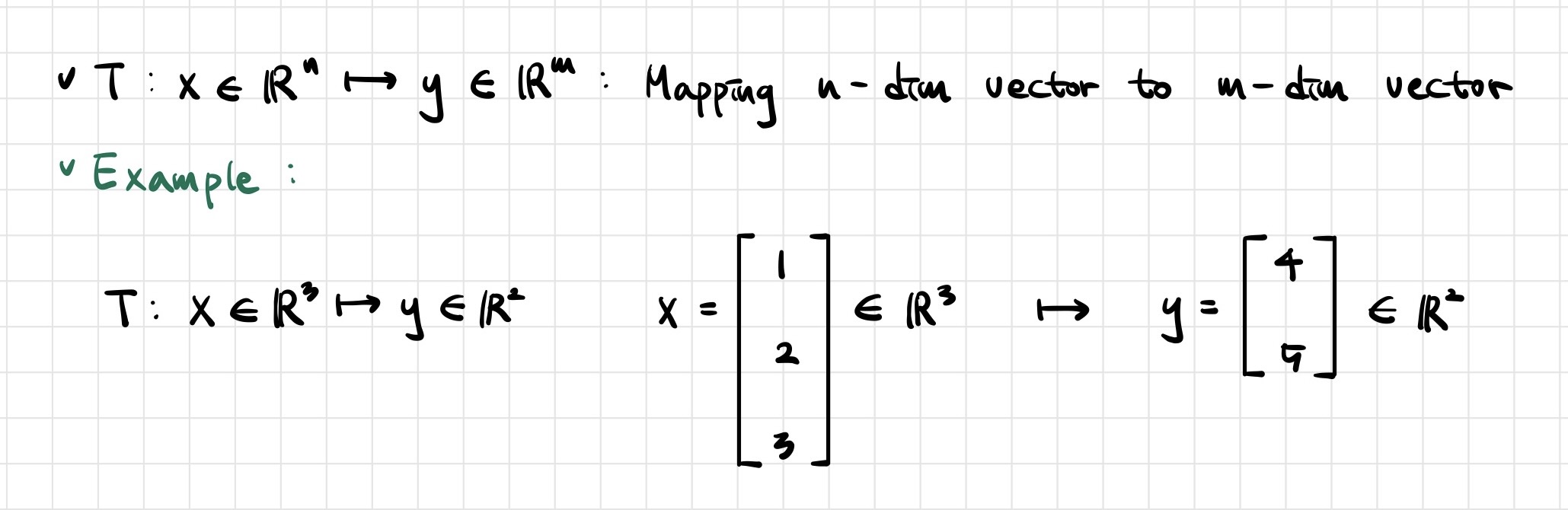
📖 Transformation between Vectors

📖 Matrix of Linear Transformation

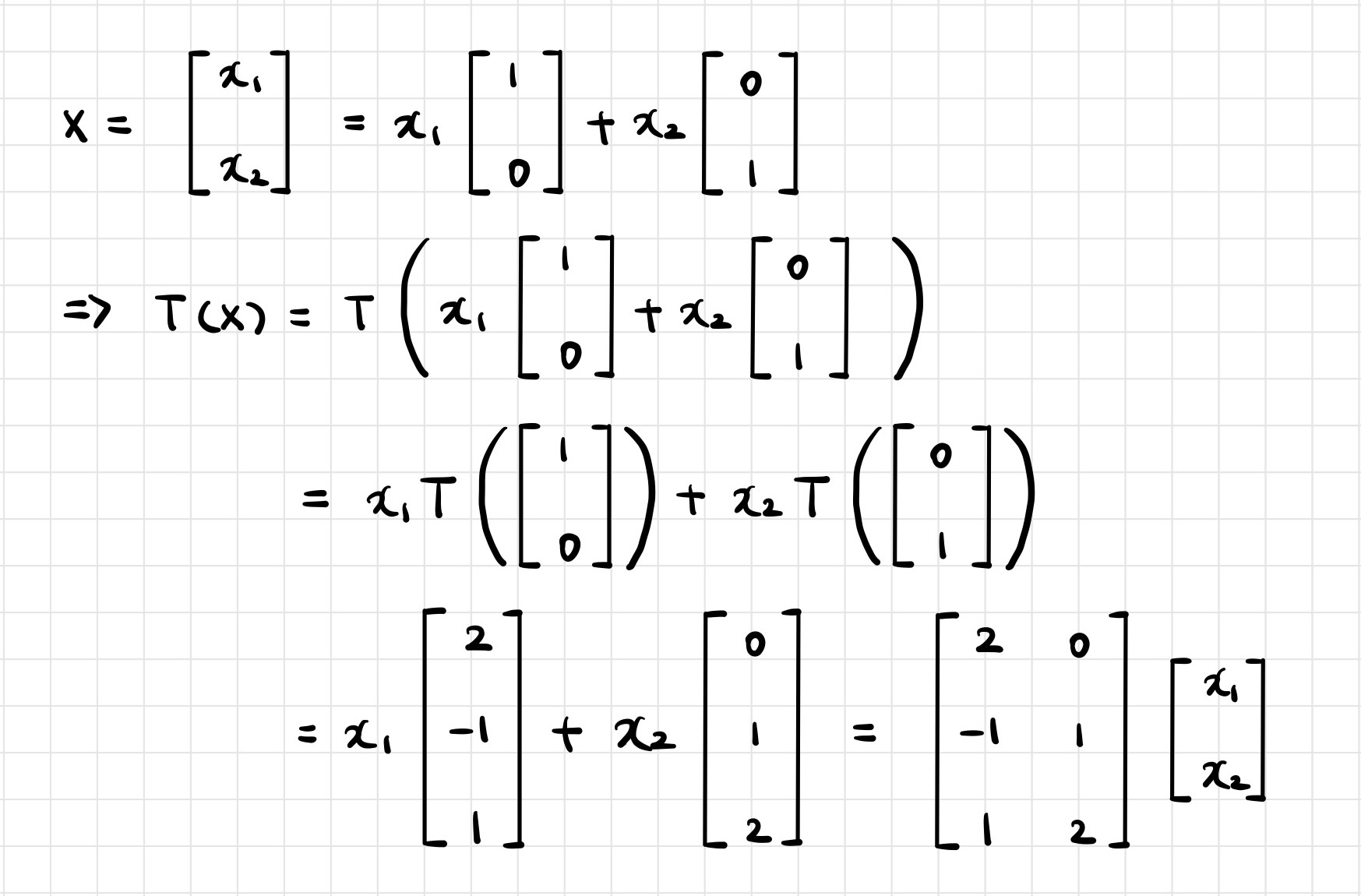
• In general, let $𝑇 ∶ R^𝑛$ → $R^𝑚$ be a linear transformation. Then $𝑇$ is always written as a matrix-vector multiplication, i.e.,
• In fact, the 𝑗-th column of $𝐴 ∈ R^{𝑚\times𝑛}$ is equal to the vector $𝑇(e_j)$ ,where $e_j$ is the 𝑗-th column of the identity matrix in $R^{𝑚\times𝑛}$ :
• Here, the matrix 𝐴 is called the standard matrix of the linear transformation $𝑇$

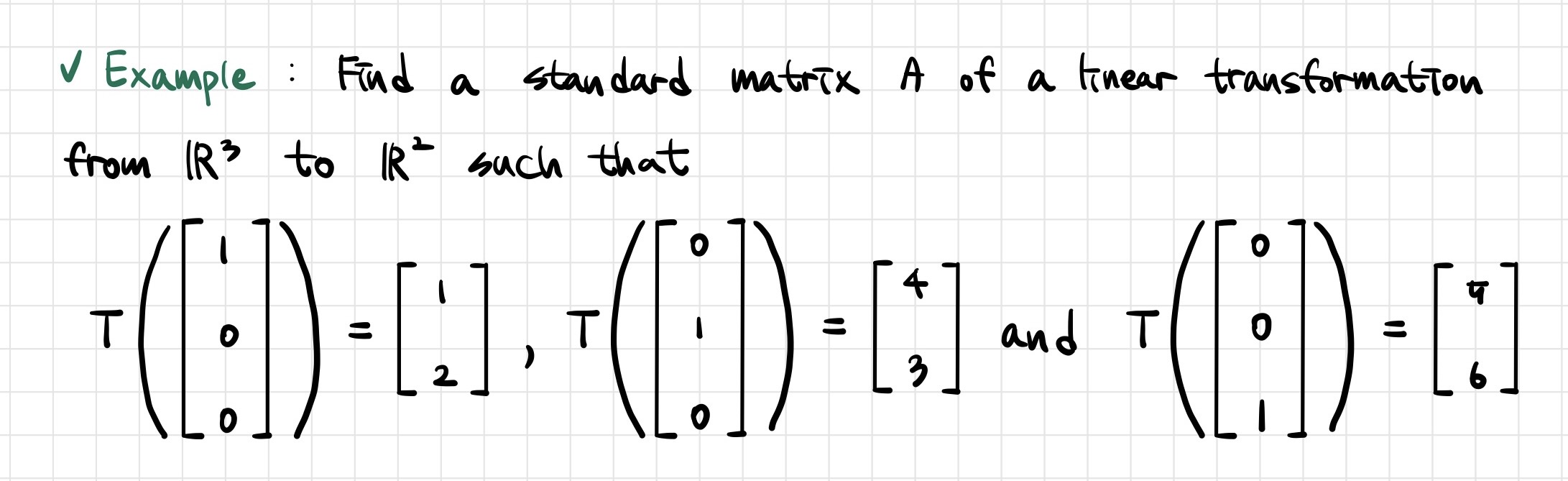
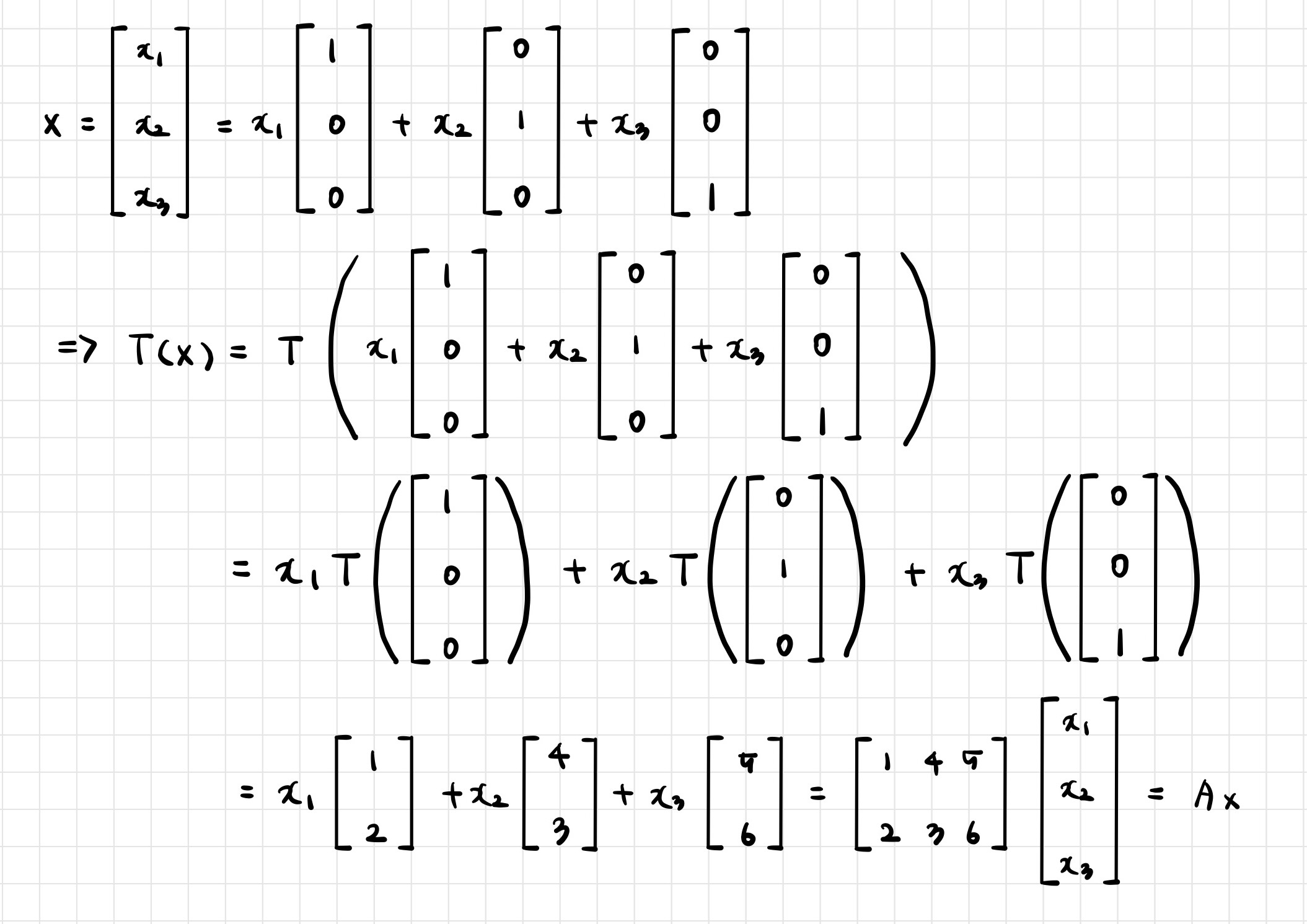
<이 게시물은 주재걸 교수님의 '선형 변환' 강의 자료를 참고하여 작성되었습니다.>

본 포스트의 학습 내용은 [부스트캠프 AI Tech 5기] Pre-Course 강의 내용을 바탕으로 작성되었습니다.
부스트캠프 AI Tech 5기 Pre-Course는 일정 기간 동안에만 운영되는 강의이며,
AI 관련 강의를 학습하고자 하시는 분들은 부스트코스 AI 강좌에서 기간 제한 없이 학습하실 수 있습니다.
(https://www.boostcourse.org/)