[통계학] 라이브 세션 3회차_t-r검정, 카이제곱검정 실습해보기

contents

• t-test 실습하기
• 카이제곱검정 실습하기

summary

# 라이브러리 호출 
import pandas as pd
import numpy as np 
# 과학 계산용 파이썬 라이브러리 
import scipy.stats as stats
from PIL import Image

# 데이터 로드
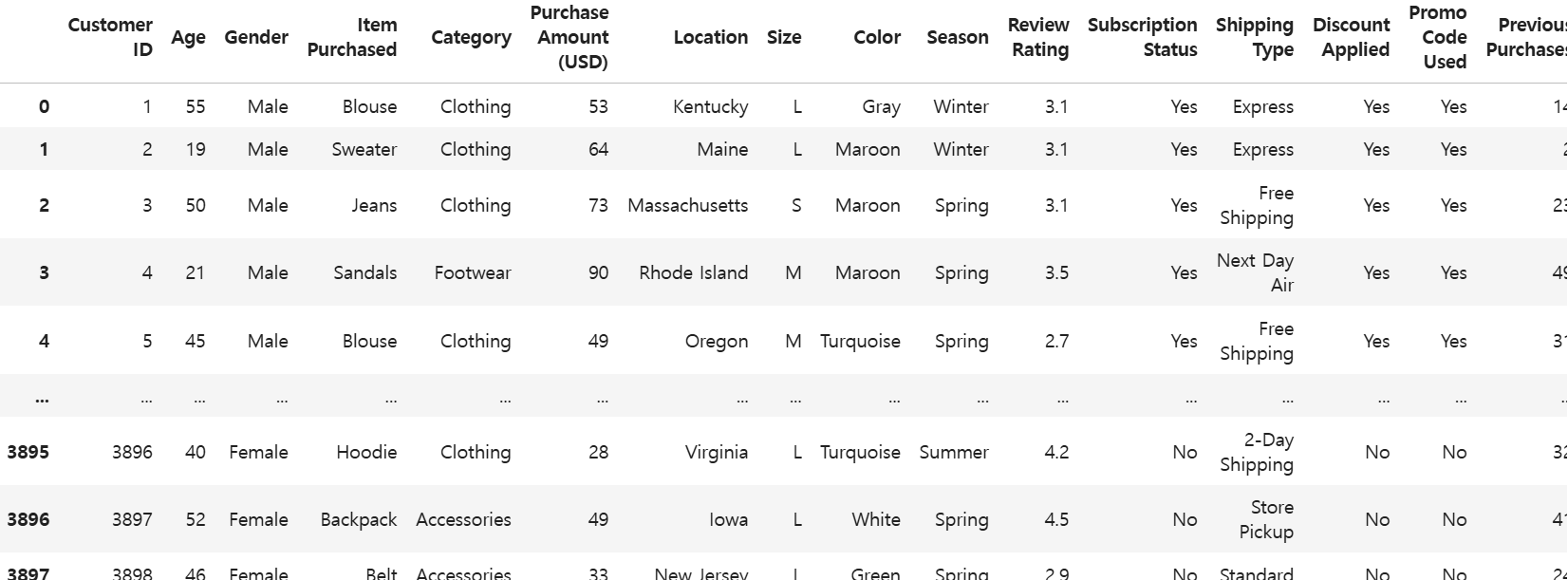
df = pd.read_csv('./statistics.csv')
df

1. t-test 실습하기
   :표본의 평균 비교/ 모집단의 분산을 모를때 연속형 자료에 사용한다.
   

• T-TEST: 가설 설정하기
  가설 설정
  귀무가설: 남성과 여성의 평균 리뷰점수에 차이가 없을 것이다
  대립가설: 남성과 여성의 평균 리뷰점수에 차이가 있을 것이다

# 실제 데이터 비교
df.groupby(['Gender'])['Review Rating'].mean().reset_index()

;실제 데이터를 뜯어본 결과 성별에 따라 평균 리뷰 점수의 차이가 거의 없는 것을 확인할 수 있다. 하지만 이를 확인하기 위해 t-test를 수행한다.

# 데이터 분리 
# mask method 
mask=(df['Gender']=='Male')
mask1 = (df['Gender']=='Female')

m_df = df[mask]
f_df = df[mask1]

# 리뷰점수 컬럼만 가져오기 
m_df=m_df[['Review Rating']]
f_df=f_df[['Review Rating']]

• T-TEST: 가설검정
  t-score 는 그룹 간 얼마나 차이가 있는지에 대한 지표
  t-score 가 크면 그룹 간 차이가 큼을 의미합니다.
  p-value 는 우연에 의해 나타날 확률에 대한 지표입니다.
  p-value가 0.05 보다 크다 = 우연히 일어났을 가능성이 높다 = 연관성이 없다고 추정

# scipy 라이브러리를 이용해 t-score 와 pvalue 를 확인할 수 있습니다. 
# t-test 는 표본의 평균(차이 분석)을 알고자 할 때 사용되며, 모집단의 분산을 알 수 없는 경우 주로 사용됩니다. 
t, pvalue=stats.ttest_ind(f_df, m_df)
t, pvalue

(array([-0.50971475]), array([0.61028017]))

• 결과 해석
  : 여기서 p-value 값은 0.05 보다 크므로, 연관성이 없다고 추정할 수 있습니다. 대립가설 기각, 귀무가설 채택 즉, 성별에 따라 평균 리뷰점수의 차이는 없을 것이다. 즉, 성별과 리뷰 점수는 서로 유의미한 관계를 보이지 않는다.

2. 카이제곱검정 실습하기

• 카이제곱검정: 가설 설정하기(범주형)
  가설 설정
  귀무가설: 성별과 Shipping Type에는 관련성이 없을 것이다 (독립적일 것이다)
  대립가설: 성별과 Shipping Type에는 관련성이 있을 것이다

# 실제 데이터 비교
df.groupby(['Gender','Shipping Type'])['Customer ID'].count().reset_index()

:성별에 따른 Shipping Type 사이에는 차이가 있어보이지만, 보다 정확한 검정을 위해 카이제곱 검정을 시행한다.

• 카이제곱검정: 빈도표 그리기

#pandas 라이브러리의 crosstab 함수를 통해, 두 범주형 자료의 빈도표를 만들어 주겠습니다.
result = pd.crosstab(df['Gender'], df['Shipping Type'])
result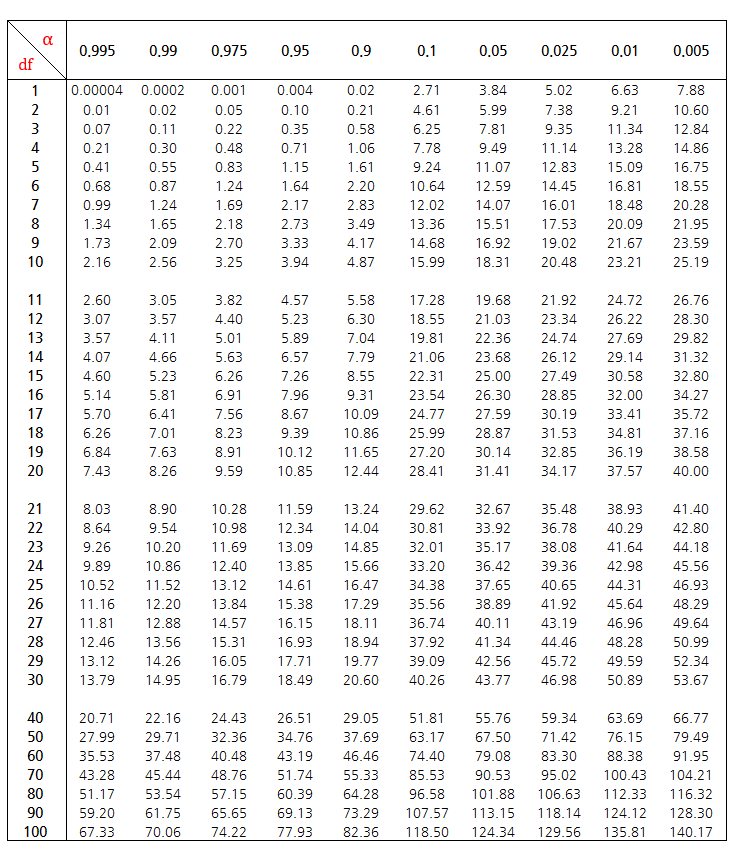

• 카이제곱검정: 가설검정

# 카이제곱 검정을 stat 함수를 통해 구현
# chi2_contingency를 통해, 카이제곱통계량, p-value를 출력할 수 있습니다.  
stats.chi2_contingency(observed=result)

Chi2ContingencyResult(statistic=12.242857409177802, pvalue=0.03160742064222473, dof=5, expected_freq=array([[200.64, 206.72, 216. , 207.36, 209.28, 208. ],
[426.36, 439.28, 459. , 440.64, 444.72, 442. ]]))

# 각 값들을 별도로 보기
# 카이제곱 검정 통계량, pvalue, 자유도를 확인할 수 있습니다. 
stats.chi2_contingency(observed=result)[0]

12.242857409177802

stats.chi2_contingency(observed=result)[1]

0.03160742064222473

->여기서 p-value 값은 0.05 보다 작으므로, 연관성이 있다고 추정할 수 있습니다.
대립가설 채택, 귀무가설 기각 즉, 성별과 Shipping Type에는 관련성이 있을 것이다. 유의미한 관계가 있을 것으로 보입니다.

• 카이제곱검정: 가설검정2

#자유도와 유의수준을 통해 귀무가설 기각 여부를 판단하기도 합니다. 
#자유도란, 굉장히 복잡한 개념이므로,,, (변수1 그룹의 수-1)*(변수2 그룹의 수-1) 가 되겠습니다. 
#(성별 2개 - 1 ) * (Shipping Type 6개 -1 ) 
# 1*5 = 5 이 도출되었습니다. 
stats.chi2_contingency(observed=result)[2]

5

• 해설
  x 축은 유의수준, y 축은 자유도 입니다.
  자유도5, 유의수준을 0.05 로 본다면, 11.07 검정통계량이 나오게 됩니다.
  우리가 구한 카이제곱 검정통계량은 12.24 이므로 11.07 보다 큽니다.¶
  표에 명시된 기준보다 값이 클 경우 대립가설을 채택합니다.
  대립가설 채택.
  이렇게까지는 잘 하지 않습니다..p-value 로 판단합니다.

• 카이제곱분포표
  

key points

분석을 진행하기에 앞서 EDA를 통해 먼저 직접 데이터가 어떤지 확인해봐야한다. 그리고 검정을 수행하고 결과를 해석한다.
하지만 통계적 분석의 결과를 100%신뢰할 수 는 없다. 직접적인 결과과 통계검정에서 같은 결과를 보일지라도 완전한 확신의 결과라고는 단언할 수 없다. 위에서 성별과 리뷰점숭 평균에는 큰차이가 없는 것을 확인했지만, 정말 관계가 없을까? 하는 생각을 반드시 해보는것이 중요하다!