[Paper Review] Conditional Density Estimation for Tabular Data Synthesis using Masked Language Modeling

yeorurirurariru·2025년 5월 31일

Paper Review

목록 보기
1/6
post-thumbnail

Abstract

본 논문의 목표 : MLu가 높은 이질적인 tabular data set에 대한 합성 데이터를 생성하는 것.
MLu의 성능은 조건부 분포를 정확하게 근사하는 것에 달려 있기 때문에, 조건부 분포 추정에 기반한 합성 데이터 생성 방법을 고안하는 데 초점을 맞춤.

접근방법?
MaCoDE => Masked Language Modeling (MLM)의 연속적인 다중 클래스 분류 과제를 히스토그램 기반의 비모수 조건부 밀도 추정으로 재정의함으로써 소개 가능

임의의 조합의 타겟 및 조건 변수에 대한 조건부 밀도를 추정할 수 있게 된다.
우리는 분포 학습과 MLM 사이의 이론적 간극을, 순서가 없는 다중 클래스 분류 손실을 최소화하는 것으로 이어짐을 입증함으로써 연결한다.

제안 모델 검증 방법?
10개의 실제 데이터셋에서 합성 데이터 생성 성능을 평가, 재학습 없이도 데이터 프라이버시 수준을 쉽게 조절할 수 있는 능력을 입증.

MLM에서 마스킹된 입력 토큰은 누락된 데이터와 유사하므로, 우리는 누락된 값을 포함하는 학습 데이터셋을 다루는 데 있어 이 모델의 효과성을 multiple imputation까지 포함해 평가함.

Introduction

synthetic tabular data generation을 위한 주요 목표
  1. 원본 데이터셋의 통계적 특성을 보존하는 것
  2. 원본 데이터셋과 비슷한 수준의 머신러닝 유용성을 달성하는 것
    -> 높은 MLu 성능을 가지는 합성 데이터 생성에 초점을 맞춘다.

MLu 성능은 어떻게 하면 높일 수 있을까?
-> 조건부 분포를 얼마나 정확하게 근사하는가에 달려 있으므로, 우리는 조건부 분포 추정 기반의 합성 데이터 생성 방법에 집중.

tabular data의 특성

1. mixed-type의 데이터로 구성
표형 데이터의 이질적인 속성을 고려하고, 연속형 열의 다양한 분포를 모델링하는 데 수반되는 어려움을 해결하기 위해, 우리는 다중 클래스 분류 과제를 기반으로 한 히스토그램 기반 비모수 조건부 밀도 추정 방식을 사용한다.

tabular data의 이질적 속성, 연속형 열의 다양한 분포 모델링 하기 위해서는 !!!
히스토그램 기반 비모수 조건부 밀도 추정 방식을 사용함.
why?
모든 열 유형에 대해 'classification loss'를 균일하게 적용할 수 있어서

단, 히스토그램 기반 비모수 조건부 밀도 추정 방식을 사용하려면 조건이 있음.
연속형 변수가 유한한 범위를 가질 때 이론적으로 유효하므로, 연속형 열을 CDF를 통해 [0,1]구간으로 정규화해 변환해야함.

2. column 간에 내재된 순서가 존재하지 않음.

MLM을 사용하는 이유? column의 생성 순서가 임의적이라는 점을 반영해야함.
maksing scheme + BERT model architecture 활용
-> 타겟 및 조건 변수의 임의 조합에 대한 조건부 밀도 추정을 가능하게 함.

이와 비슷한 방법은 없었나?
TabMT라는 유사한 방법 있으나, 이는 마스킹된 항목의 K-means clustering에 의존하기 때문에 분포 학습에는 한계가 존재.

접근법의 특이한 점 ?

열 순서를 고정해 데이터를 생성하는 기존의 auto-regressive 밀도 추정기들과는 다르며, 입력이 아닌 모델의 가중치를 마스킹하는 방식을 택한 기존 연구들과도 구별.

즉, 열의 순서를 고정하지 않음 + 입력을 마스킹함

따라서, MLM의 연속적인 다중 클래스 분류 과제를 히스토그램 기반 비모수 조건부 밀도 추정으로 재정의.

MaCoDE (Masked Conditional Density Estimation)

본 연구의 주요 기여?
distributional learning 과 MLM 내에서의 다중 클래스 분류 손실 최소화 간의 이론적 간극을 메우는 것.

  1. 여기서 multi-class classification인 이유?
    조건부 밀도 추정을 분류 문제로 바꿈.
    즉, 연속형 변수의 값을 히스토그램에서의 bin으로 바꿔서 각 구간을 class로 보고 multi-class classification 문제로 해결

  2. 히스토그램 방식을 쓰는 이유

  • 범주형 분류 문제로 변환 가능
    연속형 변수에 대한 조건부 밀도 추정 문제 -> 다중 클래스 분류 문제
    MLM(BERT)구조 그대로 사용 가능
  • 모델이 예측할 출력 형태가 명확함
  • 비모수 방식 -> 특정 분포 가정을 안함.
  • 히스토그램 기반 분류 손실을 최소화하는 것이 Total Variation Distance를 최소화하는 것과 연결.

일반성을 잃지 않고, 여기서 conditional density function을 고려할 수 있다.
우리의 주요 목표는 조건부 밀도 함수 식을 추정하는 것이다.

  1. 연속형 열의 non-uniform 분포를 모델링하는 문제
  2. 조건 변수의 임의 조합을 다루는 문제

여기서 가역은 내생각엔 뒤에 이 F함수가 CDF인데 한 변수에 대해서 무조건 한 값을 가져야 하기 때문에 가역 (=역함수 존재) 라고 가정한 것 같고,
미분가능하다는 가정은 CDF를 미분해서 PDF (여기서는 conditional density function)을 얻어야 하기 때문에 그런 것 같음.

-> 이 가정이 필요한 이유?

x라는 연속형 변수의 conditional density function을 추정해야 하는데, 식을 CDF에 대한 조건부 밀도 함수를 추정하는 것으로 변환해야 하기 때문임.

즉, 이 변환이 가능한 이유는 모든 열에 대해 Fj가 가역이고 미분가능하다고 가정했기 때문임.

그리고 여기서는 위의 두 문제를 히스코그램 기반 조건부 밀도 추정 방법 + MLM 접근법을 통해 해결.

연속형 데이터에 대해 조건부 확률을 어떻게 추정할 것인가?

  1. 연속형 열의 분포가 일정하지 않음.
  2. 조건 변수로 들어가는 feature들의 조합이 매우 다양함.
  • 데이터를 CDF로 변환해서 다루기 쉽도록 만든다. (CDF는 [0.1]범위로 데이터를 정규화한다.)

3.1 Classification Target(Discretization)

이산화를 하는 이유? MLM 기반 접근법은 multi-class classification에 의존하기 때문이다. tabular data의 각 열인 x -> label (분류 대상) y

히스토그램 기반 접근법을 사용하기 위해서 필요한 것 ?
-> 연속형 열이 유한한 구간 안에 있어야 함. CDF를 통해 각 열을 [0,1]로 변환.

[0,1] 구간을 L+1개의 cut points b0,b1,,,,bL로 나눈다.
즉, b0 = 0, bL = 1이라서, bin의 개수 (구간) 는 L개가 만들어진다.

The Discretization Function

즉, 실수 공간에서 이산 공간으로 변형하는 이산화 함수를 만들었다는 뜻.

3.2 Masked Conditional Density Fucntion

위에서 만든 함수가 이산화 함수였다면, 이제는 masked conditional density function을 만들어 보자. -> 앞 뒤 열의 값이 주어졌을 때, 이를 사용해서 마스킹된 값을 예측하는 것이다..


우리가 구하고자 하는 분포는 위와 같음.
xk : mk= 1 가 의미하는 것은 mk=1 즉, 마스킹되지 않은 열 ( = Xk) 이 주어졌을 때
이산화함수가 (우리가 구하고자 하는 값인) l일 확률을 구하고 싶은 것임.

이를 다시 써보면 다음과 같이 정의된다.

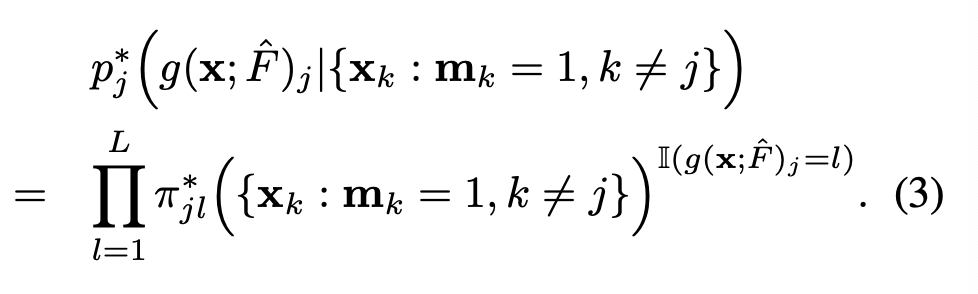
확률을 곱하는 것인데, 여기서 이산화함수가 우리가 찾는 l값일 경우의 확률을 다 곱해주는 것과 의미가 같다고 할 수 있다.

⊙ 는 원소별 곱 (element-wise multiplication) -> 즉, 마스크된 입력을 의미함.
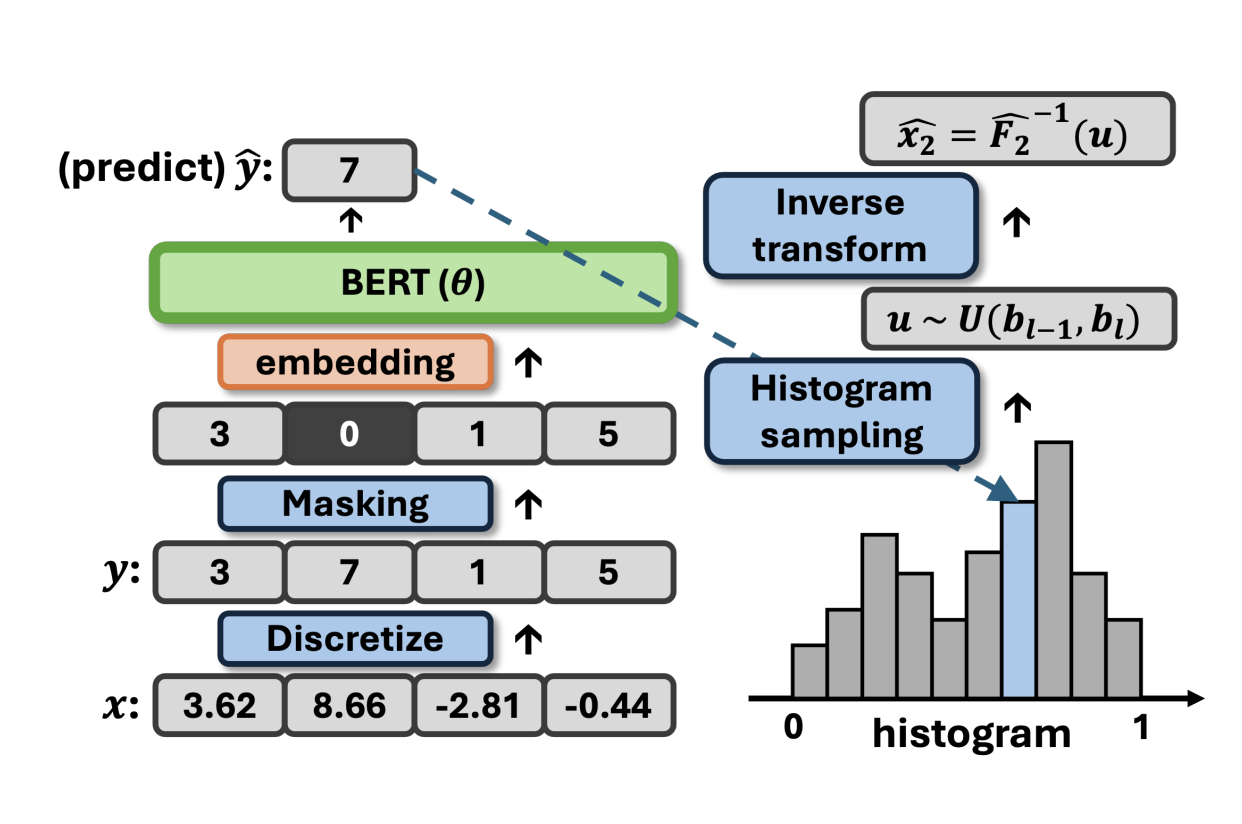
이게 뭐하는 거냐면 ,,, 아래의 그림을 참고하면 된다.

따라서, 이 수식은 마스킹된 입력을 바탕으로 Transformer 분류기가 예측한 다중 클래스 조건부 확률 분포를 계산하는 방식이다. 입력은 CDF를 통해 정규화되며, 관측된 값만 사용되어 예측에 반영된다. 확률 분포는 softmax 구조를 따르며, 실제 클래스에 해당하는 항만 남도록 one-hot 기반 지수 곱셈 형태로 표현된다.

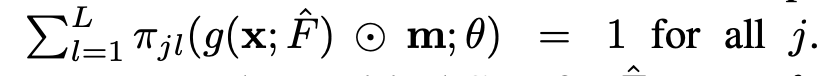
The objective function for a single observation

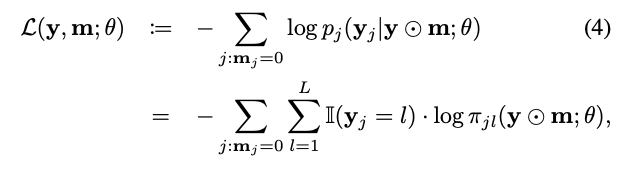
이는 마스킹된 항목의 negative log-likelihood로 정의된다.
여기서 label yj는 이산화 함수로 정의된다.
우리의 목적 함수는 각 bin에서 CDF의 조건부 분포를 추정하며, 그 목표 분포는 target distribution으로부터 얻어진 것이다.
즉, 우리의 목표는 진짜 조건부 확률을 추정된 확률로 근사하는 것이다.

MLM과의 유사성?
-> 원래의 입력 y 중 일부 항목을 마스킹하고, 모델이 그 마스킹된 항목의 값을 예측하도록 함. 즉, 문장에서 특정 단어를 가리고 그 단어를 예측하는 것처럼, 테이블의 셀을 가리고 그 값을 예측하는 방식이다.

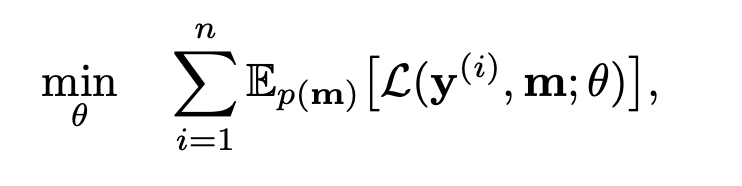
전체 알고리즘은 이와 같다.
MaCoDE에서 제안하는 알고리즘은 tabular 형식의 데이터 특성을 반영한 합성 데이터 생성 방식을 설명한다. 자연어와는 달리, 표 데이터는 열 간 순서가 존재하지 않기 때문에, MaCoDE는 임의로 섞은 열 순서에 따라 한 번에 하나의 열 씩 데이터를 생성한다.
1. 히스토그램 bin 샘플링 및 마스킹 해제
2. 데이터 값 복원

핵심 특징 및 장점

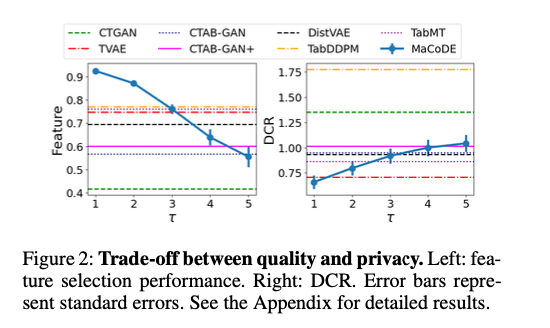
  • 조절 가능한 프라이버시 수준
    샘플링 온도를 높일 수록 분포가 평탄해져서, 보다 랜덤하고 프라이버시가 보장된 데이터를 생성할 수 있다.
    이로 인해, 모델 재학습 없이도 데이터 품질과 프라이버시 간의 균형을 조절 가능함.
  • 재학습 없이 다양한 설정 가능
    기존 방법들은 프라이버시 수준을 바꾸려면 모델을 다시 학습해야 했다.
    하지만, 이는 온도 파라미터 하나로 제어 가능함.

4.Experiments

4.1 Overview

#### Q1. Does MaCoDE acheive state - of - art performance in synthetic data generation?
#### Q2. Can MaCoDE generate high-quality synthetic data even when faced with missing data scenarios?
#### Q3. Is MaCoDE capable of supporting multiple imputations for deriving statistically valid inferences from missing data?

위의 세가지 실험 질문에 대한 답을 제공할 수 있는 실험을 수행함.
첫번째 질문은 합성 데이터 생성에서 최첨단 성능을 달성할 수 있는지,
두번째 질문은 missing data가 있는 상황에서도 고품질의 합성 데이터를 생성할 수 있는지,
세번째 질문은 결측 데이터로부터 통계적으로 유효한 추론을 도출하기 위한 multiple imputation을 지원할 수 있는지

Datasets

사용한 데이터셋?

크기 및 열의 수가 다양한 10개의 공개된 실세계 UCI 및 Kaggle의 tabular 데이터셋을 사용함.

58만 개의 행을 가진 covtype 데이터셋을 포함해 제안된 모델의 확장성을 입증함.

Baseline models

여기서 baseline model은 MaCoDE와 비교되는 기존의 대표적인 모델들이다.
MaCoDE의 경우, 모든 데이터셋에 대해서 L=50, temperature parameter = 1로 설정함.

Q1과 Q2 질문에 대해서는 MaCoDE와 다음 모델들을 비교했다.

  • CTGAN (Xu et al. 2019)
  • TVAE (Xu et al. 2019)
  • CTAB-GAN (Zhao et al. 2021)
  • CTAB-GAN+ (Zhao et al. 2023)
  • DistVAE (An and Jeon 2023)
  • Tab-DDPM (Kotelnikov et al. 2023)
  • TabMT (Gulati and Roysdon 2023)

Q3 질문에 대해서는 mixed-type tabular 데이터셋에 다중 대체가 가능한 모델들을 선정해 비교한다.

  • MICE (van Buuren and Groothuis-Oudshoorn)
  • GAIN (Yoon, Jordon, and van der Schaar 2018)
  • missMDA (Josse and Husson 2016)
  • VAEAC (Ivanov, Figurnov, and Vetrov 2019)
  • MIWAE (Mattei and Frellsen 2019)
  • not-MIWAE (Ipsen, Mattei, and Frellsen 2021)
  • EGC (Zhao, Townsend, and Udell 2022)

  • 지표 해석을 돕기 위한 기준 합성 데이터셋을 포함함.
    metric을 해석하는 데 도움을 주기 위해, 실험에서는 기준 합성 데이터셋 (baseline synthetic dataset)을 포함함.
    이 데이터셋은 실제 학습 데이터의 절반을 합성 데이터로 구성한 것.

soft upper bound : 현실적인 최상의 기준선, 이보다 좋은 성능은 기대하기 어려운 점수.

temperature parameter : 데이터 생성 모델에서 다양성과 프라이버시를 조절하는 중요한 하이퍼 파라미터. (클수록 생성 데이터의 무작위성이 증가 -> 좋은 것)

민감도 분석 (sensitivity) : 결측률이 다를 때 모델의 성능이 어떻게 변하는지 분석하는 과정.

4.2 Evaluation Metrics (평가 지표)

모든 실험에 대해 우리는 10개의 서로 다른 random seed와 10개의 데이터셋에 대해서 mean, standard error를 막대 그래프로 보고함.

각 랜덤 시드마다, 데이터셋은 80% 학습 + 20% 테스트 비율 무작위 분할. -> 1,2번 질문에 사용.

평가 중, 합성 데이터셋은 실제 학습 데이터셋과 동일한 샘플 수로 구성.

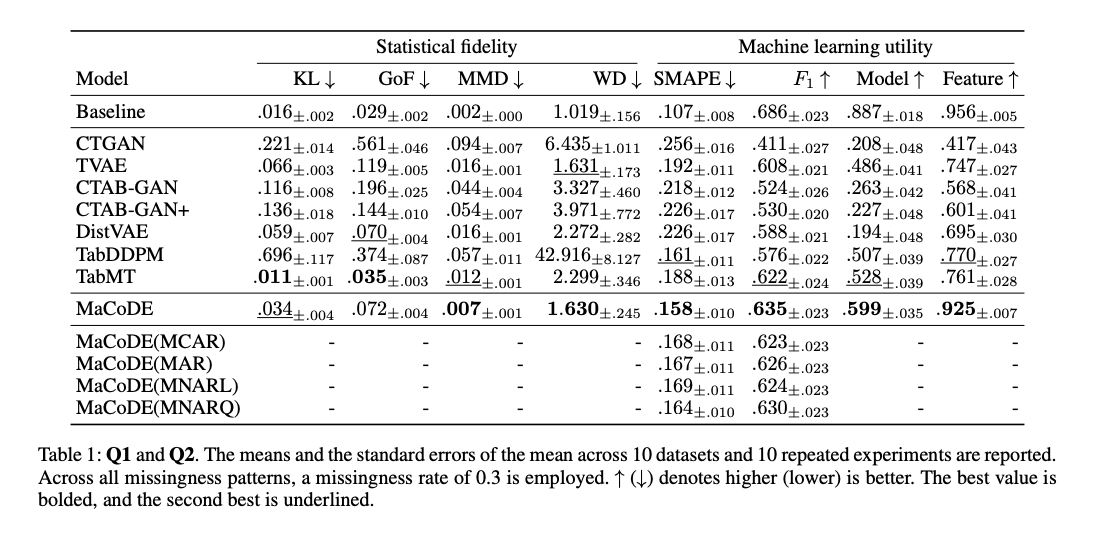
Q1. Synthetic Data Quality Evaluation

-Metric1. : Statistical Fidelity (통계적 유사도)
:실제 데이터와 합성 데이터의 분포가 얼마나 비슷한 지 측정
- KL Divergence (Kullback-Leibler 발산) -> 어떤 분포 p,q가 있을 때 이들이 얼마나 비슷한 분포인지 표현하는 measure, 분포의 entropy와 비교하는 분포 간의 cross entropy값을 반영한다.
- Goodness-of-Fit (GoF) 검정
연속형 데이터 : Kolmogorov - Smirnov (KS) 이표본 검정 통계량
범주형 데이터 : 카이제곱 검정 통계량
- MMD (Maximum Mean Discrepancy)
- WD (1-Wasserstein Distance)
-Metric2. : MLu (Machine Learning utility)
: 제안된 모델이 생성한 합성 데이터를 가지고 학습했을 때 성능을 측정.
4가지 지표 (Hansen et al. 2023에서 제안됨):
-회귀 성능 (SMAPE: 대칭 평균 절대 백분율 오차)
-분류 성능 (F₁-score)
-모델 선택 성능 (Model)
-특징 선택 성능 (Feature)

Q2. 결측값 상황에서 고품질 합성 데이터 평가

모델이 결측값이 존재하는 상황에서도 고품질 합성 데이터를 생성할 수 있는지 평가함.
이를 위해, 결측값이 있는 훈련데이터를 기반으로 모델을 학습시킨 후, 합성 데이터를 생성하고 테스트 세트에서 회귀 및 분류 성능을 평가한다.
전체 훈련 데이터가 필요한 다른 평가 지표들과는 달리, 테스트 세트만으로 평가가 가능한 지표를 사용해 성능을 비교한다.

Q3. Multiple Imputation의 효과 평가

: bias, coverage, the length of confidence interval

평가지표를 좀 정리해 보아씀.

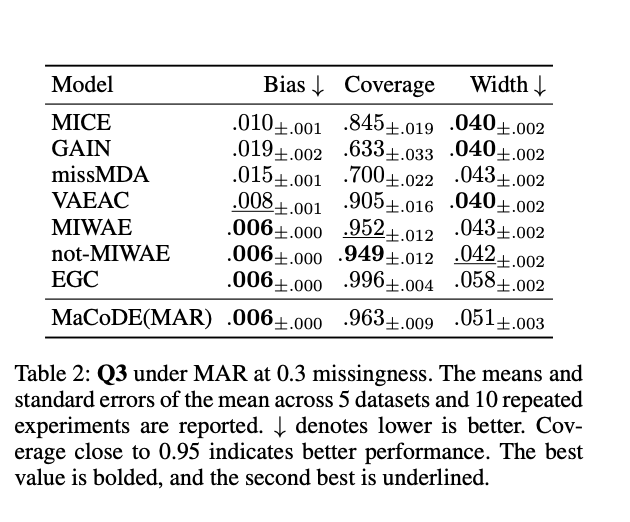
위 결과는 다중 대체 성능 평가를 보여주는 것으로, missing rate 30%인 MAR(Missing At Random) 조건 하에서 수행된 실험이다. 이 실험은 5개의 데이터셋에 대해 10회 반복해서 평균과 표준오차를 보고하고 있다.

-> MaCoDE 모델은 편향이 매우 낮음. -> 대체된 값의 평균이 실제 평균가 크게 다르지 않음
-> 신뢰구간 coverage도 기준치를 초과함 -> 신뢰구간이 실제 평균을 포함하는 비율이 높음
-> 신뢰구간의 평균길이 적절함

4.3 Results

#### Q1. 합성 데이터 품질 평가 결과 - MaCoDE는 통계적 분포 유사성 및 머신러닝 유틸리티 측면에서 항상 가장 높은 성능을 기록함. - feature selection을 포함한 다운스트림 머신러닝 작업에서도 우수한 성능을 보임. - 이는 MaCoDE가 조건부 분포 기반의 합성 데이터 생성 방법을 통해 원본 데이터의 통계적 충실도를 유지하면서도, 학습 모델을 위한 합성 데이터를 효과적으로 생성할 수 있음. - 특히, feature selection downstream task에서 뛰어난 성능을 입증함.

여기서 feature selection 성능이 좋은 이유?
-> MaCoDE가 조건부 분포를 정확히 추정하기 때문

Q2. missing data에서의 성능

  • 결측 데이터 유형 ? (MCAR: 완전 무작위 결측, MAR: 무작위 결측, MNAR: 비무작위 결측)
  • 결측률이 존재하는 상황에서도 고품질 합성 데이터를 생성하고, 머신러닝 성능 저하 없이 테스트셋에서 좋은 결과를 냄.

Q3. Multiple Imputation 성능

MaCoDE는 bias, coverage, CI 길이 기준으로 모든 비교 모델들과 유사하거나 더 우수한 성능을 보임. -> 이는 결측 데이터부터로의 통계적으로 유효한 추론을 가능하게 한다는 뜻.

5. Conclusions and Limitations

결론.

이 논문은 tabular data를 위한 새로운 합성 데이터 생성 접근 방식을 제안한다.
제안한 MaCoDE 모델은

  • 비매개적 조건부 밀도 추정을 기반
  • MLM 기반 접근 방식과 통합.
  • high statistical fidelity + Machine learning utility 모두 달성

실험 결과

다양한 결측 메커니즘 상황에서도 고품질 합성 데이터 생성

한계점

MaCoDE는 현재 Lipschitz 연속성 가정 하에서 작동한다. 따라서 연속형 분포의 폭넓은 범위를 다루는 데 한계가 존재함.

따라서 앞으로의 과제는 ?

  • 더 다양한 연속형 분포를 수용하는 모델 확장
  • Lipschitz 연속성 가정을 넘는 일반화된 구조 설계가 필요함.
profile
yeorurirurariru
다음 포스트

[Paper Review] Deep Learning based Recommender System : A Survey and New Perspectives

0개의 댓글