Manifold

Manifold?

manifold는 고차원 데이터가 있을 때 이 데이터를 잘 아우르는 저차원 구조를 의미합니다.고차원 공간 속에서 데이터가 놓여 있는 복잡하고 비선형적인 저차원 구조를 manifold라고 하며 이를 통해 다양한 효과를 기대합니다.

Manifold Learning을 사용하는 이유

1. Data Compression
2. Data Visualization
3. Curse of Dimensionality
4. Discovering most important features

1. Data Compression

Variational Autoencoders, Neural Image Compression with Recurrent Neural Networks, End-to-end Optimized Image Compression 등의 논문에서는 JPEG 방식보다 Manifold learning을 통해 더 효율적인 압축이 가능하다는 것을 보여주고 있습니다. 특히 VAE는 단순한 압축을 넘어 데이터의 분포를 학습하여 잠재 공간에서 새로운 데이터를 생성할 수 있는 능력을 제공합니다. 이와 같은 Autoencoder 기반의 모델들은 고차원 데이터를 저차원 잠재 공간으로 매핑하여 데이터의 중요한 정보를 보존하면서도 효율적으로 압축할 수 있습니다.

2. Data Visualization

Manifold Learning은 데이터를 시각화하는 데 매우 유용합니다. 대표적으로 t-SNE나 UMAP같은 방법들이 manifold learning을 통해 데이터를 저차원으로 시각화하는 데 사용됩니다. 이러한 시각화는 데이터에 대한 직관적인 이해를 높이며 머신러닝 결과물에 대한 해석하는데 도움이 됩니다.

3. Curse of Dimensionality

먼저 차원의 저주란 데이터의 차원이 증가할수록 해당 공간의 크기가 기하급수적으로 증가하기에 동일한 개수의 데이터의 밀도는 차원이 증가할수록 급속도로 희박해집니다.
따라서 차원이 증가할수록 데이터의 분포를 분석하거나 모델 추정에 필요한 샘플 데이터의 개수가 기하급수적으로 증가하게 됩니다.
이렇게 정보량이 희박한 상황에서 모델링을 진행하게 되면 예측값이 잘 나오지 않는 경우가 많습니다.
그래서 고차원의 공간에서 데이터를 잘 아우르는 subspace를 찾게 되면 데이터가 잘 밀집되어 있는 훌륭한 차원을 찾아낼 수 있습니다.

👏 즉, 고차원 데이터의 밀도는 낮지만, 이들의 집합을 포함하는 저차원의 매니폴드가 있을 것이고 이 저차원의 매니폴드를 벗어나는 순간 급격히 밀도는 낮아집니다.

manifold 공간은 본래 고차원 공간의 subspace이기에 차원 수가 상대적으로 작아집니다.
이는 차원 축소(Dimension Reduction)를 가능케합니다.
차원 축소가 잘 되었다면 이는 매니폴드 공간을 잘 찾았다는 것을 의미합니다.
본래 고차원 공간에서 각 차원들을 잘 설명하는 새로운 특징을 축으로 하는 공간을 찾았다는 뜻으로 해석할 수 있습니다.

4. Discovering most important features

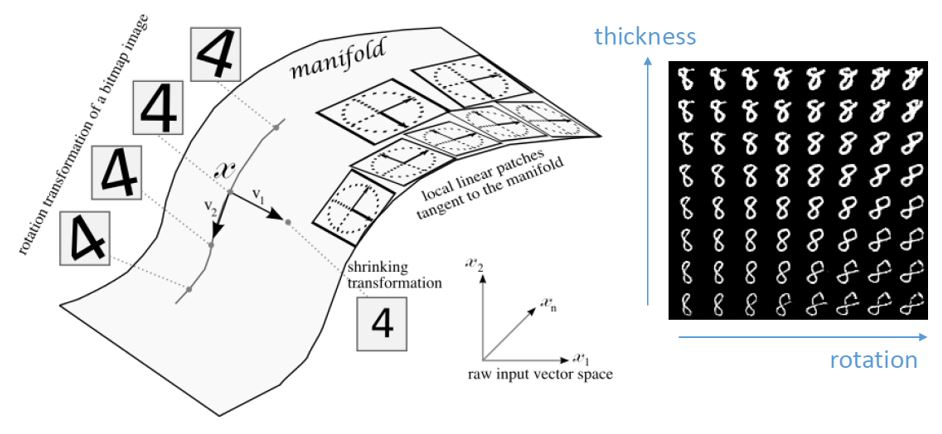
위 그림은 MNIST 손글씨 데이터 입니다. 이는 28 * 28의 784차원 이미지 데이터입니다.
이 데이터를 2차원으로 축소하였을 때 x축은 rotation 회전, y축은 thickness 두께를 나타냅니다.
매니폴드 공간에서 이 두 개의 축은 두 개의 특징(feature)을 의미하고 이를 변경하게 되면 변화되는 이미지 형태를 획득할 수 있습니다.

👏 고차원 데이터의 manifold 좌표들을 조정해보면 manifold의 변화에 따라 학습 데이터도 유의미하게 조금씩 변화는 것입니다.

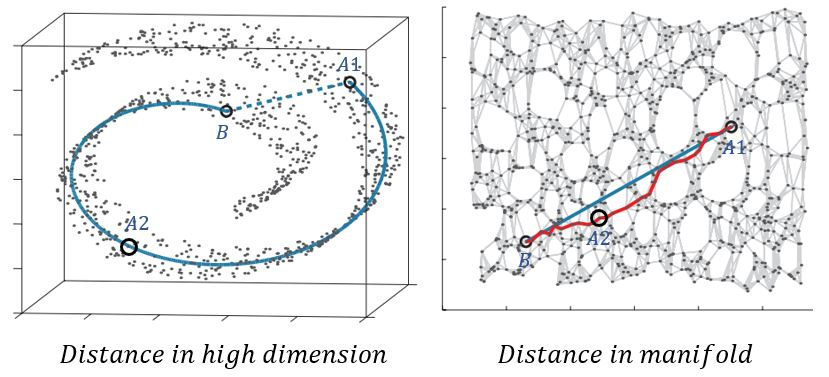
고차원 공간에서 보면 상대적으로 B와 A1사이의 거리는 B와 A2사이의 거리보다 가깝습니다.
그러나 manifold 공간에서는 A2가 A1보다 B에 더 가깝습니다.
이는 이미지 데이터 픽셀 간의 거리는 A1과 B가 더 가까울 수 있으나 의미적인 유사성 관점에서는 A2와 B가 더 가까울 수 있다는 것을 이야기합니다.

위의 이미지를 보시면 중간의 그림을 좌우 그림을 통해 예측한 것입니다.
왼쪽의 고차원 공간에서 이미지는 팔과 골프채가 2개로 좌우 이미지 픽셀의 중간을 보여주고 있고 오른쪽의 manifold 공간에서 이미지는 의미적으로 중간에 있는 모습을 보여주고 있습니다.
이렇듯 manifold를 잘 찾으면 의미적인 유사성을 잘 보존할 수 있고 유사한 데이터를 획득하여 학습 데이터에 없는 데이터를 획득할 가능성 또한 열리게 됩니다.