Option을 나눌 때, 이분법적으로 보기 위해서는 Path-Independent-Option과 Path-Dependent-Option 두 가지로 보는 것이 편합니다.
이번 장에서는 Path-Dependent-Option에 대해 알아 볼 거예요.
Path-Dependent-Option에는 여러 가지 종류가 있는데요, 크게 Complex- Path-Dependent-Option이랑 Exotic-Path-Dependent-Option으로 나눠져요.
그 중에서도 우리가 식을 만들어서 이해할 수 있는 부분은 Exotic 한 거라서..
왜냐하면, 대부분 우리가 Black-Scholes 공식을 이용해서 옵션의 가치를 구할 수 있겠지만, 실무에서는 반드시 표준화된 내용으로 계약이 이루어지지 않기 때문에, 조금 수정된 형태의 Exotic Option을 주로 이용해요.
그럼 Exotic Option의 종류를 알아봅시다.
Digital Option
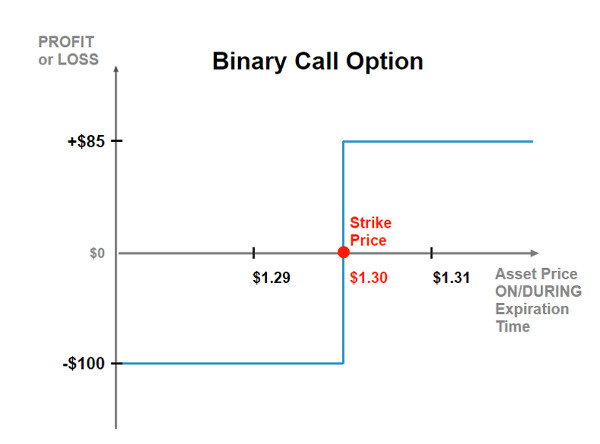
디지털 옵션은 비연속적인 현금 흐름을 갖는 옵션입니다.
디지털 콜 옵션은 주가가 행사가격 이상으로 상승하면, 사전에 약정한 일정 금액 (Q Q Q
반대로, 디지털 풋 옵션은 주가가 행사가격 아래로 내려가면, 사전에 약정한 일정 금액을 받는 옵션입니다.
매도자가 많아도, 일정 가격 이하로는 팔려고 하지 않고, 매수자도 일정 수준 이하로 가격이 낮아지지 않는 이상 사려고 하지 않는 상황에서, 매수 또는 거래 포기 둘 중 하나를 선택하도록 구조화된 양자 택일형 옵션.
좀 극단적이죠?.. 그래서 하나의 독립된 상품으로 거래되기 보다는 여러 가지 형태의 옵션과 조합을 이루어서 거래되는 것이 보통입니다.
그림에서 보시다시피, 이진법의 Binary를 붙여서 Binary Call Option이라고 이야기하기도 합니다.
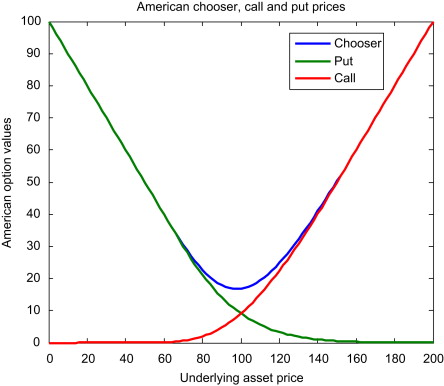
Chooser Option
매입 시점에는 콜/풋 여부를 정하지 않고, 매입 후 일정 시점에 가서 매입자가 유리한 방향으로 콜/풋 여부를 선택할 수 있도록 한 옵션.
(중요) Barrier Option
배리어 옵션은 옵션의 잔존기간동안 기초 자산의 가격이 계약 시점에 미리 정해놓은 일정한 수준에 도달하는가에 따라 Payoff가 결정되는 옵션입니다.
기본적인 형태로 Knock-In 옵션과 Knock-Out 옵션이 있는데요,
Knock-In Option : 기초 자산의 가격이 정해진 배리어에 도달할 때부터 옵션의 효력이 발생한다.
Knock-Out Option : 기초 자산의 가격이 정해진 배리어에 도달하면 옵션으로서의 효력이 소멸되어 버린다.
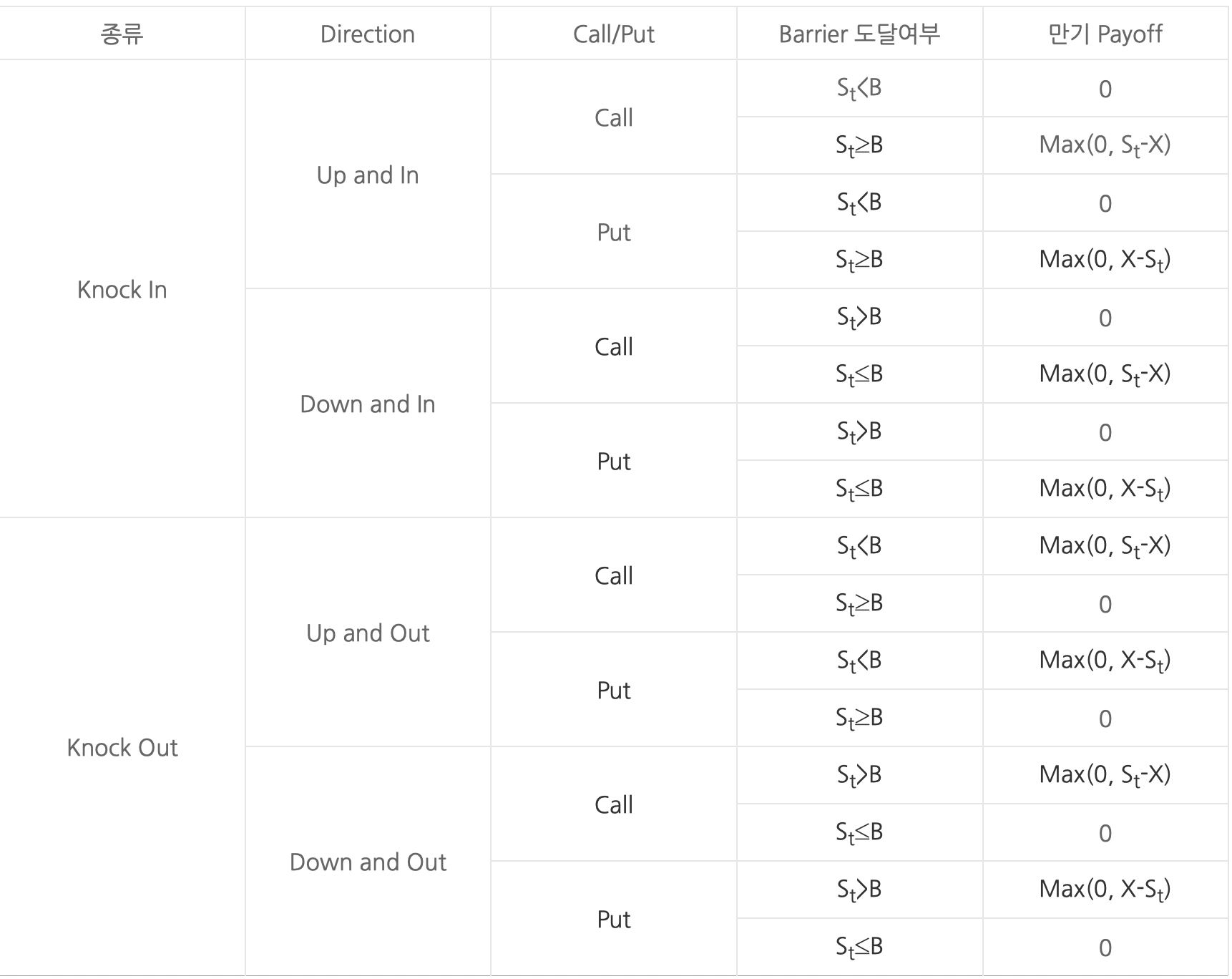
기초 자산의 가격이 하락하면서 도달하면 Down-and-In, Down-and-Out, 상승하면서 도달하면 Up-and-In, Up-and-Out.. 이렇게 얘기해요.
표를 가져오면,
이렇게 16가지의 Payoff가 존재하겠네요.
(중요) Asian Option
아시안 옵션은 행사 또는 만기 시 Payoff가 옵션의 잔존기간동안의 기초자산의 평균가격에 의존하는 옵션입니다. 이 평균 가격을 어떻게 구하느냐에 따라서, Arithmetic Asian Option과 Geometric Asian Option이 나눠집니다.
우리가 이미 알고 있듯이, 콜옵션의 payoff는 max ( 0 , S a v g − K ) \max(0,S_{avg} - K) max ( 0 , S a v g − K )
그런데 위에 설명했듯이, 저 S a v g S_{avg} S a v g
우리가 만기일 T와 strike price(목표가) K를 가지고 있다고 해봅시다.
Geometiric Asian Option
Geometric Average 는
G T = ( ∏ i = 1 N S t i ) 1 N G_T = (\prod_{i=1}^N S_{t_i})^{\frac 1 N} G T = ( i = 1 ∏ N S t i ) N 1 이렇게 구할 수 있을거고요.
우리는 계산의 편의성을 위해, 기초 자산의 가격이 log-normal distribution을 따른다고 하면, 산술 평균은 log-normal distribution을 따른다고 이야기할 수는 없겠지만.. 기하 평균은 log-normal dist.를 따른다고 이야기할 수 있어요.
그러면.. Black-Scholes 공식을 사용하여 풀 수 있겠네요.
C G E O M E T R I C − A s i a n = exp ( − r T ) ( exp ( a + 1 2 b ) N ( x ) − K N ( x − b ) ) C_{GEOMETRIC-Asian} = \exp (-rT) (\exp (a+\frac 1 2 b)N(x) - KN(x-\sqrt {b})) C G E O M E T R I C − A s i a n = exp ( − r T ) ( exp ( a + 2 1 b ) N ( x ) − K N ( x − b ) ) a = ln ( G t ) + N − m N ( ln ( S ) + ν ( t m + 1 − t ) + 1 2 ν ( T − t m + 1 ) ) a = \ln (G_t) + \frac {N-m} N (\ln (S) + \nu (t_{m+1} - t) + \frac 1 2 \nu (T - t_{m+1})) a = ln ( G t ) + N N − m ( ln ( S ) + ν ( t m + 1 − t ) + 2 1 ν ( T − t m + 1 ) ) b = ( N − m ) 2 N 2 σ 2 ( t m + 1 − t ) + σ 2 ( T − t m 1 ) 6 N 2 ( N − m ) ( 2 ( N − m ) − 1 ) b = \frac {(N-m)^2} {N^2} \sigma^2 (t_{m+1} - t) + \frac {\sigma^2 (T - t_{m_1})} {6N^2} (N-m) (2(N-m)-1) b = N 2 ( N − m ) 2 σ 2 ( t m + 1 − t ) + 6 N 2 σ 2 ( T − t m 1 ) ( N − m ) ( 2 ( N − m ) − 1 ) ν = r − δ − 1 2 σ 2 \nu = r- \delta - \frac 1 2 \sigma^2 ν = r − δ − 2 1 σ 2 x = a − ln ( K ) + b b x = \frac {a - \ln (K) + b} {\sqrt {b}} x = b a − ln ( K ) + b 여기서 G t G_t G t m m m
Arithmetic Asian Option
그럼 이 때, Arithmetic Average 는
A T = 1 N ∑ i = 1 N S t i A_T = \frac 1 N \sum_{i=1}^N S_{t_i} A T = N 1 i = 1 ∑ N S t i 로 구할 수 있고,max ( 0 , A T − K ) \max(0,A_T - K) max ( 0 , A T − K )
Turnbull & Wakeman's Approximation
위의 설명에서, 산술평균은 log-normal distribution을 따르지 않기 때문에 Black-Scholes를 못 쓴다고 했었죠?
이러한 문제를 해결하기 위해, Turnbull & Wakeman은 산술평균의 1,2차 적률을 계산하고, 산술평균이 이와 같은 적률을 가지는 log-normal distribution을 가진다고 가정하여 Asian Option의 근사값을 구하려고 했어요.
위의 C G E O M E T R I C − A s i a n C_{GEOMETRIC-Asian} C G E O M E T R I C − A s i a n
옵션의 가치는
C = exp ( − r t ) [ M 1 N ( d 1 ) − X N ( d 2 ) ] C = \exp (-rt) [M_1 N(d_1) - XN(d_2)] C = exp ( − r t ) [ M 1 N ( d 1 ) − X N ( d 2 ) ] Payoff는
P = exp ( − r t ) [ X N ( − d 2 ) − M 1 N ( − d 1 ) ] P = \exp (-rt) [XN(-d_2) - M_1N(-d_1)] P = exp ( − r t ) [ X N ( − d 2 ) − M 1 N ( − d 1 ) ] where
M 1 = exp ( ( r − q ) t ) − 1 ( r − q ) t S M_1 = \frac {\exp((r-q)t) - 1} {(r-q)t} S M 1 = ( r − q ) t exp ( ( r − q ) t ) − 1 S M 2 = 2 exp ( [ 2 ( r − q ) + σ 2 ] t ) S 2 ( r − q + σ 2 ) ( 2 r − 2 q + σ 2 ) t 2 + 2 S 2 ( r − q ) t 2 ( 1 2 ( r − q ) + σ 2 − exp ( ( r − q ) t ) r − q + σ 2 ) M_2 = \frac {2 \exp ([2(r-q)+\sigma^2]t) S^2} {(r-q+\sigma^2) (2r-2q+\sigma^2)t^2} + \frac {2S^2} {(r-q)t^2} (\frac 1 {2(r-q)+\sigma^2} - \frac {\exp ((r-q)t)} {r-q+\sigma^2}) M 2 = ( r − q + σ 2 ) ( 2 r − 2 q + σ 2 ) t 2 2 exp ( [ 2 ( r − q ) + σ 2 ] t ) S 2 + ( r − q ) t 2 2 S 2 ( 2 ( r − q ) + σ 2 1 − r − q + σ 2 exp ( ( r − q ) t ) ) σ A 2 = 1 t ln ( M 2 M 1 2 ) {\sigma_A}^2 = \frac 1 t \ln ( \frac {M_2} {{M_1}^2}) σ A 2 = t 1 ln ( M 1 2 M 2 ) d 1 = l n ( M 1 X ) + σ A 2 t 2 σ A t d_1 = \frac {ln (\frac {M_1} X) + \frac {\sigma_A^2 t} 2} {\sigma_A \sqrt {t}} d 1 = σ A t l n ( X M 1 ) + 2 σ A 2 t d 2 = d 1 − σ A t d_2 = d_1 -\sigma_A \sqrt{t} d 2 = d 1 − σ A t 여기서 M 1 M_1 M 1 M 2 M_2 M 2
Clicket (Ratchet) Option
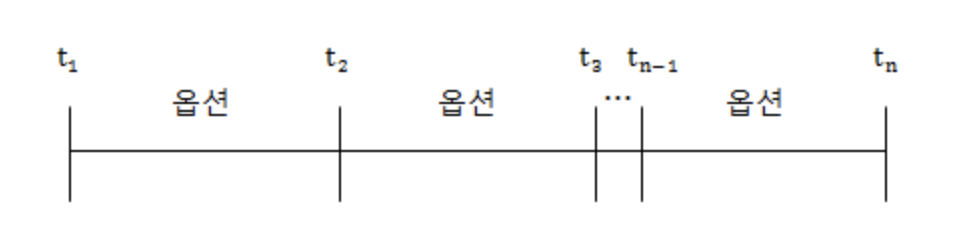
클리켓 옵션(래칫 옵션)은 옵션의 잔존 기간동안 일정한 시점마다 행사가격을 주기적으로 재설정하는 옵션입니다.
즉, 재설정 시점의 기초자산 가격을 새로운 행사가격으로 설정하여 다음 재설정 시점까지의 행사가격으로 사용하는 것입니다.
재설정 시의 옵션의 내재가치는 이미 실현된 것으로 간주하여 옵션 발행자는 옵션 매입자에게 그 지급을 보장하게 됩니다. 옵션의 가격은 연속적인 옵션의 합으로 구할 수 있습니다.
C = ∑ i = 1 n − 1 S exp ( − q t i ) [ exp ( − q ( t i + 1 − t i ) ) N ( d 1 ) − exp ( − r ( t i + 1 − t i ) ) N ( d 2 ) ] C = \sum_{i=1}^{n-1} S \exp(-qt_i) [\exp(-q(t_{i+1} - t_i)) N(d_1) - \exp(-r(t_{i+1} - t_i)) N(d_2)] C = i = 1 ∑ n − 1 S exp ( − q t i ) [ exp ( − q ( t i + 1 − t i ) ) N ( d 1 ) − exp ( − r ( t i + 1 − t i ) ) N ( d 2 ) ] P = ∑ i = 1 n − 1 S exp ( − q t i ) [ exp ( − r ( t i + 1 − t i ) ) N ( − d 2 ) − exp ( − q ( t i + 1 − t i ) ) N ( − d 1 ) ] P = \sum_{i=1}^{n-1} S \exp(-qt_i) [\exp(-r(t_{i+1} - t_i)) N(-d_2) - \exp(-q(t_{i+1} - t_i)) N(-d_1)] P = i = 1 ∑ n − 1 S exp ( − q t i ) [ exp ( − r ( t i + 1 − t i ) ) N ( − d 2 ) − exp ( − q ( t i + 1 − t i ) ) N ( − d 1 ) ] d 1 = ( r − q + σ 2 2 ) ⋅ ( t i + 1 − t i ) σ t i + 1 − t i d_1 = \frac {(r-q+\frac {\sigma^2} 2) · (t_{i+1} - t_i)} {\sigma \sqrt {t_{i+1} - t_i}} d 1 = σ t i + 1 − t i ( r − q + 2 σ 2 ) ⋅ ( t i + 1 − t i ) d 2 = d 1 − σ t i + 1 − t i d_2 = d_1 - \sigma \sqrt {t_{i+1} - t_i} d 2 = d 1 − σ t i + 1 − t i Lookback Option
룩백 옵션은
콜옵션의 경우, 보유자가 만기일 이전에 실현된 기초자산의 가격 중, 가장 낮은 가격으로 매입할 수 있고,
약간 가격이 비싸다는 단점이 있지만, 아메리칸 옵션에서 발생할 수 있는 '행사오류', 유러피안 옵션에서 만기에만 권리를 행사함으로서 발생할 수 있는 '최적유동성의 실현불가능성'을 만회할 수 있습니다.
위의 설명에 의하면, Payoff는
max ( 0 , max ( S t i ; i = 1 , . . . , N ) − K ) \max(0,\max(S_{t_i} ; i = 1,...,N)-K) max ( 0 , max ( S t i ; i = 1 , . . . , N ) − K ) 가 될 거고요.
이제 기초자산의 가격과 분산을 계산해볼까요?
이 기초자산의 가격에 대한 분산이 V = σ 2 V = \sigma^2 V = σ 2
그러면 우리는 Stochastic Differential Equations (SDE)
d S = r S d t + σ S d z 1 dS = rS dt + \sigma S dz_1 d S = r S d t + σ S d z 1 d V = α ( V ‾ − V ) d t + ξ V d z 2 dV = \alpha (\overline{V} - V)dt + \xi \sqrt{V} dz_2 d V = α ( V − V ) d t + ξ V d z 2 를 얻을 수 있는데요, 이 때 d z 1 dz_1 d z 1 d z 2 dz_2 d z 2
Wiener Process :Δ t \Delta t Δ t Δ t \Delta t Δ t
Volatility가 constant하다고 가정하면,
C c a l l = G + S exp ( − δ T ) N ( x + σ T ) − K exp ( − r T ) N ( x ) − S B ( exp ( − r T ) ( E S ) B N ( x + ( 1 − B ) σ T ) − exp ( − δ T ) N ( x + σ T ) ) C_{call} = G+S\exp(-\delta T)N(x+\sigma \sqrt{T}) - K\exp(-rT)N(x) - \frac S B (\exp (-rT) (\frac E S)^B N(x+(1-B)\sigma \sqrt{T}) - \exp(-\delta T) N(x+\sigma \sqrt{T})) C c a l l = G + S exp ( − δ T ) N ( x + σ T ) − K exp ( − r T ) N ( x ) − B S ( exp ( − r T ) ( S E ) B N ( x + ( 1 − B ) σ T ) − exp ( − δ T ) N ( x + σ T ) ) Where
E = K , G = 0 ( K ≥ M ) E = K , G= 0 (K\geq M) E = K , G = 0 ( K ≥ M ) E = M , G = exp ( − r T ) ( M − K ) ( K < M ) E = M , G = \exp(-rT) (M-K) (K<M) E = M , G = exp ( − r T ) ( M − K ) ( K < M ) B = 2 ( r − δ ) σ 2 B = \frac {2(r-\delta)} {\sigma^2} B = σ 2 2 ( r − δ ) x = ln ( S E ) + ( ( r − δ ) − 1 2 σ 2 ) T σ T x = \frac {\ln (\frac S E) + ((r-\delta) - \frac 1 2 \sigma^2) T} {\sigma \sqrt {T}} x = σ T ln ( E S ) + ( ( r − δ ) − 2 1 σ 2 ) T 이렇게 가치평가를 할 수 있습니다.
다음 게시물에서는 Random number를 만드는 방법에 대해서 이야기해볼게요.