1.5 Hedge sensitivities , Multiple stochastic Factors

Woohyuk Choi·2022년 7월 10일

금융공학

금융상품 가치 측정

목록 보기

5/6

오랜만에 글을 쓰게 됐네요. 이런 저런 일들이 겹쳐서 요즘 공부를 별로 하지 못했는데 이제부터라도 화이팅해서 해보도록 하겠습니다.

Hedge Sensitivities

우리는 이제 선물 Option에 대해 생각하려고 합니다. 일차원적인 선물계약에서는 진입 가격과 이후 시장에서 올랐는지 내렸는지에 따라 손익이 결정되지만, 옵션에서는 이야기가 좀 달라요.

이렇게 다양한 변동성이 존재합니다. (출처 : CME Groups , Option Delta)
이러한 다양한 지표들이 존재해요.
결국 말 그대로, Hedging을 할 때의 민감도를 나타내는 여러 지표들을 소개하려 합니다.
Delta, Gamma, Vega, Theta, Rho 이렇게 다섯 가지의 지표들이 존재하는데요,
각각이 무엇인지 한 번 볼까요?

Delta

먼저 델타부터 봅시다.

Delta : 기초가 되는 선물 가격의 변화로 인해 옵션 가격, 프리미엄에 생기는 변화.

수식으로 나타내면 이렇게 돼요.

delta = \frac {\partial C} {\partial S} \approx \frac {{C(S+\vartriangle S)} -{C(S -\vartriangle S)}} {2\vartriangle S}

예를 들어, 현재가가 1.00 이고, 델타 값이 0.50인 콜 옵션이 있다고 해봅시다. 델타 값이 여기서 의미하는 바는, "기초 자산인 '선물'의 변동폭이 얼마이건 간에, 나는 그 변동폭의 50%만 움직일래 !" 이걸 의미해요.

만약 선물 가격이 96에서 97.5로 상승했다면, 선물 가격의 변동폭은 1.5가 되겠죠? 여기서 델타 값을 적용하면 옵션 가격의 변동폭은 0.75가 될거고, 결국 옵션 가격은 1.75가 되겠네요.

콜 옵션의 델타값 : 0 ~ +1.00
풋 옵션의 델타값 : -1.00 ~ 0
선물 계약의 델타값 : 1.00

여기서 예시를 들면, 델타가 0.25인 콜 옵션 8개의 계약을 매도했다고 해봅시다. 그럼 여기서 델타 포지션은 -2.00이 되겠네요. 이걸 중립으로 만드려면 2개의 기초 선물 계약을 매수해서, 델타값을 0으로 만드는 방법을 택해야 하겠죠? 이런 식으로 중립을 유지합니다.

그런데, 콜 옵션에 롱 포지션을 가지면 양의 델타값이 나오겠지만, 숏 포지션을 가지면 음의 델타값이 나오겠네요. 풋 옵션도 숏 포지션을 가지면 양의 델타값이 나오고요.

Gamma

이제 감마를 볼까요?

이걸 설명하기 전에, 우리는 내가격, 외가격, 등가격에 대해 알아야 해요.

내가격 : 콜옵션에서 기초자산(지수·종목) 가격이 행사가격보다 높을 때(풋옵션에선 낮을 때)

등가격은 두 가격이 같을 때, 외가격은 내가격의 반대라고 생각하면 쉬울 것 같습니다.

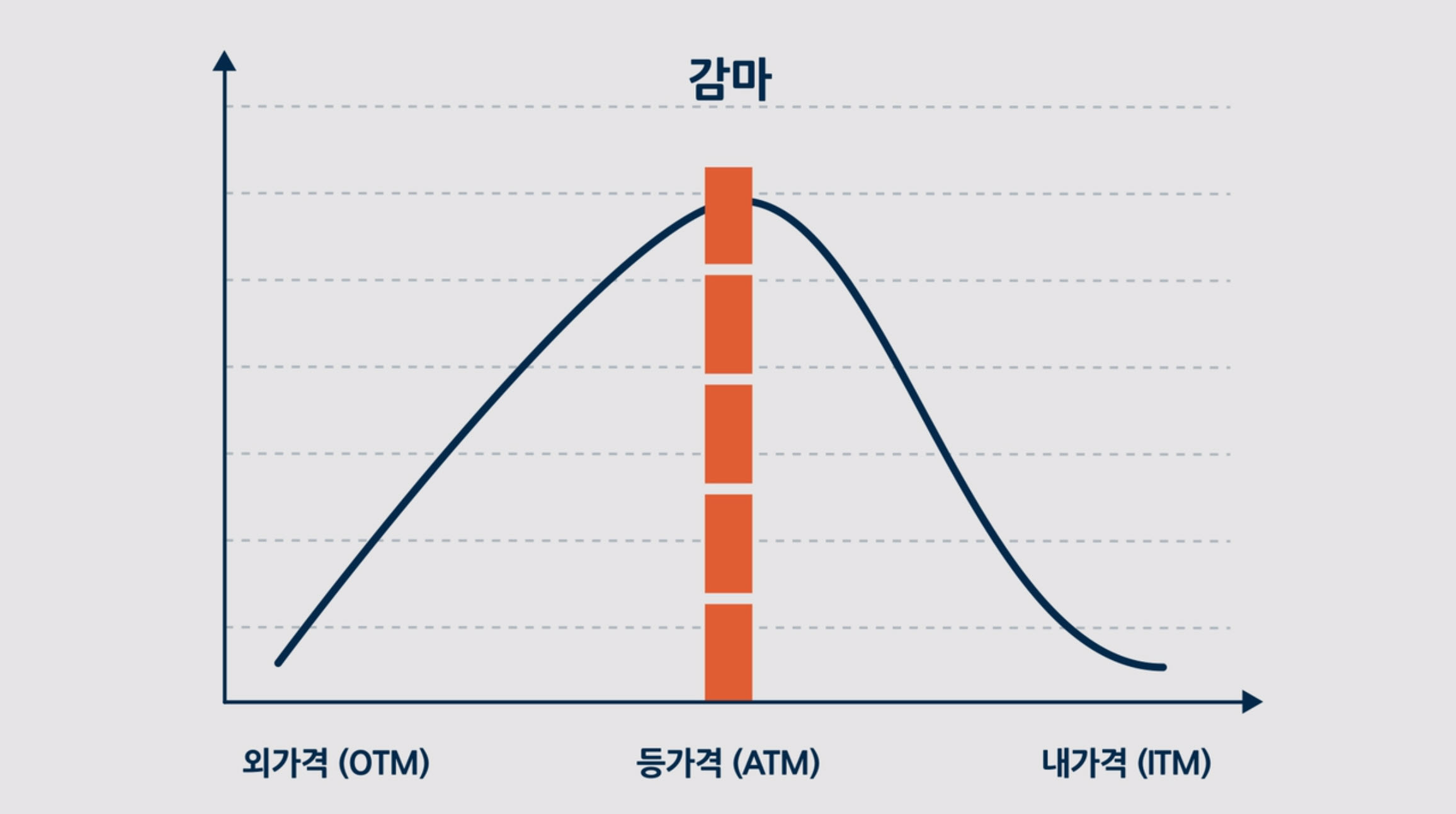
그렇다면 감마는 무엇일까요?

Gamma : 기초 선물 가격이 변할 때, 델타의 변화량.

gamma = \frac {\partial^2 C} {\partial S^2} \approx \frac {{C(S+\vartriangle S)} -2C(S)+{C(S -\vartriangle S)}} {\vartriangle S^2}

위의 정의와 같이, 감마는 보통 기초자산 가격의 1포인트 변화 당 델타의 변화로 나타냅니다.

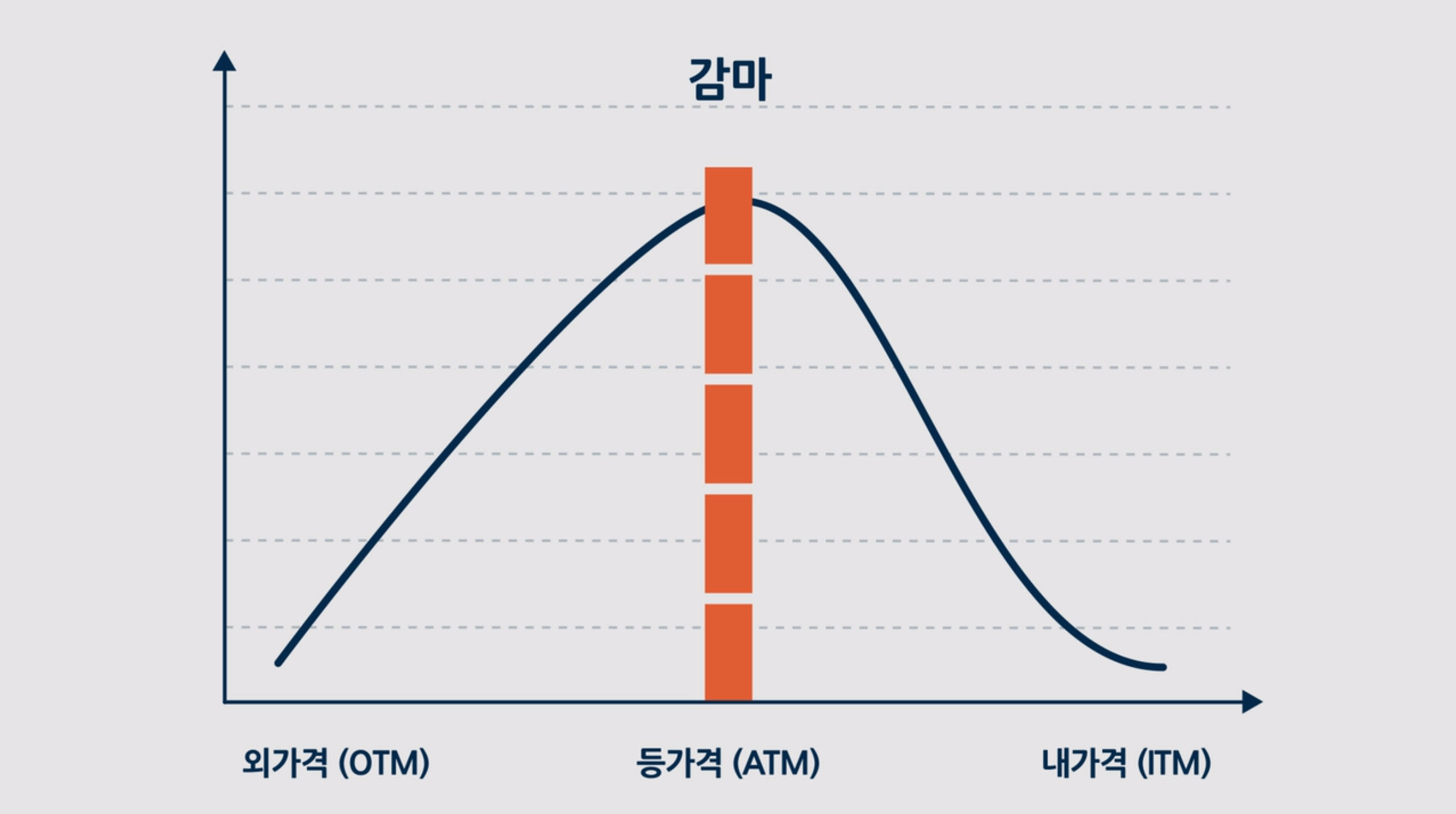
위 그래프를 보면 알 수 있듯, 등가격 옵션의 감마가 제일 높고, 멀어질수록 감마가 감소하는 것을 알 수 있습니다.

Vega

다음으로 우리가 볼 지표는 베가 입니다.

Vega : 내재 변동성에 대한 옵션의 민감도

vega = \frac {\partial C} {\partial \sigma} \approx \frac {{C(\sigma +\vartriangle \sigma)} -{C(\sigma -\vartriangle \sigma)}} {2\vartriangle \sigma}

예를 들어, 내재 변동성이 20에서 21.5로 변한다고 가정하면, 변동성이 1.5 증가한 것이 되겠죠? 이 때, 옵션의 베가값이 0.12라고 하면, 변동성의 변화인 1.5에 0.12를 곱한 0.18이 베가 효과가 되어 이전의 프리미엄 값에 0.18을 더해줘야 한다.. 이렇게 이해하면 될 것 같아요.

베가는 기초자산의 가격과 옵션 행사 가격이 같을 때, 즉 등가격일 때 가장 높고, 만기에 가까워질수록 하락하는 특징을 가집니다. 만기까지의 기간이 길수록, 옵션의 베가는 더 커집니다.

Theta

이제 세타 를 알아볼까요?

앞에서, 델타와 감마는 기초자산의 가격 변동이 옵션의 가격에 미치는 영향을 측정하는 지표였어요.

그럼 이제 우리가 궁금해지는건, 시간에 따라 얘가 어떻게 변하느냐.. 이거가 되는거죠.

Theta : 시간에 따른 옵션 가격의 민감도

그래서,

theta = \frac {\partial U} {\partial t} \approx \frac {{C(r+\vartriangle r)} -{C(t)}} {\vartriangle t}

이렇게 되고,
세타는 등가격 옵션에서 가장 크며 외가격이나 내가격의 정도가 심할수록 작아집니다.
등가격이나 등가격에 가까운 옵션에서 세타의 절대치는 옵션이 만기에 가까워질 수록 커집니다.
또, 내가격이나 외가격이 심한 옵션의 세타는 만기에 가까워질수록 작아집니다.

Rho

마지막으로 알아볼 로 는,

Rho : 이자율이 1포인트 움직임에 따라 옵션 가격이 얼마나 변하는지 측정한 값.

얘는 장기 옵션에 영향을 주고, 단기 옵션에 있어서는 큰 변화가 없습니다.

수식으로 나타내면 이렇게 돼요.

rho = \frac {\partial C} {\partial r} \approx \frac {{C(r+\vartriangle r)} -{C(r-\vartriangle r)}} {2\vartriangle r}

Psi

책에 있는 내용 말고, 하나 더 알아보면, 프사이 라는 지표도 존재하는데요,

Psi : 옵션가격의 배당의 변동에 대한 민감도

psi = \frac {\partial C} {\partial \delta}

Multiple Stochastic Factors

지금까지 우리가 얘기하고자 하는 것은 다 Monte Carlo Simulation에 대한 것이었죠?
때로는 이 복잡한 세상을 간소화해서 계산의 편의성을 도모하기도 하지만, 우리도 알다시피 이 세상은 꽤나 복잡해요..

제목에서 볼 수 있다시피, 우리는 다양한 Stochastic Factor들을 고려해야 하는데, 그 예시 중 좋은 것이 우리가 앞에서 배운 수식들이겠네요.

$S_1$ 과 $S_2$ 라는 두 자산의 차이에 대한 European Spread Option을 생각해봅시다. 우리는 Brownian Motion을 이야기 하면서 Geometric Brownian Motion $dz_1$ , $dz_2$ 을 정의했어요.

dS_1 = (r-\delta_1)S_1 dt + \sigma_1 S_1 dz_1

dS_2 = (r-\delta_2)S_2 dt + \sigma_2 S_2 dz_2

이 둘 사이의 Correlation을 $\rho$ 라고 합시다.

그럼 이 두 GBM, $dz_1$ , $dz_2$ 는 아래와 같은 관계를 가집니다.

dz_1 · dz_2 = \rho dt

그리고, 우리는 위 식의 결과를 알고 있죠? (시간을 T라 했을 때)

S_1,_T = S_1 exp(v_1 T + \sigma_1 z_1,_T) , v_1 = r-\delta_1 - \frac 1 2 \sigma_1^2

S_2,_T = S_2 exp(v_2 T + \sigma_2 z_2,_T) , v_2 = r-\delta_2 - \frac 1 2 \sigma_2^2

그리고! 우리는 지금 $dz_1$ , $dz_2$ 만 알고 있지, $z_1$ , $z_2$ 는 모르잖아요..;;

그래서 Correlation $\rho$ 를 갖는 Standard-Bivariate normal distribution을 따르는 $z_1$ , $z_2$ 를 생성해야 해요.

서로 독립인 정규분포를 따르는 $\epsilon_1$ , $\epsilon_2$ 가 있다고 하면,

z_1 = \epsilon_1

z_2 = \rho \epsilon_1 + \sqrt{1-\rho^2} \epsilon^2

이렇게 나타낼 수 있어요.

오늘은 책에 있는 내용 2개의 장을 다뤄봤는데, 이 중에서 Hedge Sensitivity를 나타내는 Option Greeks는 중요하니 복습하시는 것을 추천합니다!

Woohyuk Choi

Financial Engineering / Mathematics / Music

이전 포스트

1.4 Control Variates and Hedging

다음 포스트