깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)

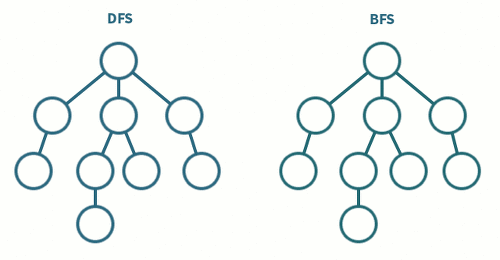
그래프를 탐색하는 방법에는 크게 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)이 있습니다.

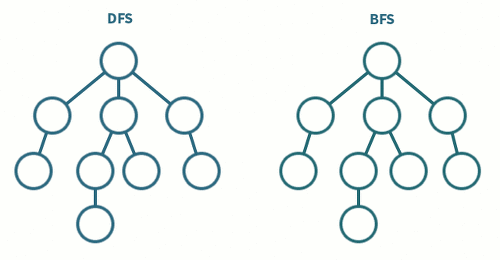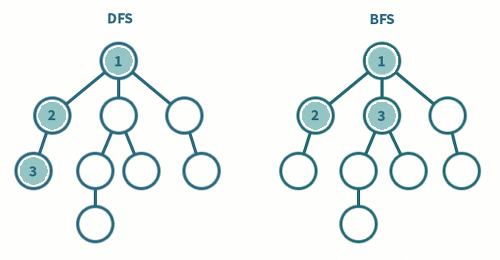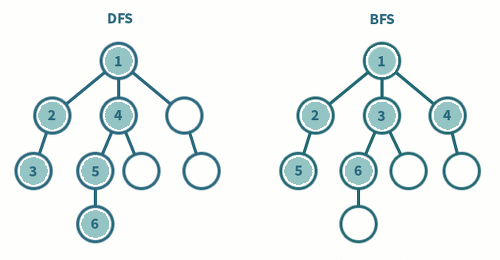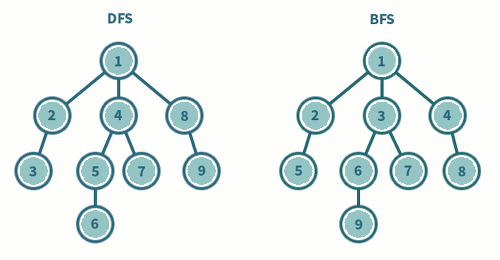
DFS(깊이우선탐색)	BFS(너비우선탐색)
현재 정점에서 갈 수 있는 점들까지 들어가면서 탐색	현재 정점에 연결된 가까운 점들부터 탐색
스택 또는 재귀함수로 구현	큐를 이용해서 구현

깊이 우선 탐색 (DFS, Depth-First Search)

한 경로의 끝까지 탐색한 후 다음 경로로 넘어가는 방식

특징

• 자기 자신을 호출하는 순환 알고리즘의 형태를 지닙니다. (재귀 or 스택)
• 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야합니다. (검사하지 않을 경우 무한루프에 빠질 수 있다. )
• 미로를 탐색할 때, 해당 분기에서 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로(새로운 분기)로 돌아와서 다른 방향으로 다시 탐색을 진행하는 방법과 유사합니다.
• 모든 노드를 방문하고자 할 때, 이 방법을 선택합니다.
• 너비우선탐색(BFS)보다 더 간단합니다.
• 검색 속도 자체는 너비우선탐색(BFS)에 비해서 느립니다.

Java로 DFS 구현

재귀(Recursion) 형태로 구현

예시 문제

https://school.programmers.co.kr/learn/courses/30/lessons/43162

public class Solution {
    // 인접 리스트를 사용한 그래프 표현
    List<List<Integer>> adjList = new ArrayList<>();
    boolean[] visited;

    public int solution(int n, int[][] computers) {
        int answer = 0;
        visited = new boolean[n];

        // 인접 리스트 초기화
        for (int i = 0; i < n; i++) {
            adjList.add(new ArrayList<>());
        }

        // 인접 리스트 구성
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (i != j && computers[i][j] == 1) {
                    adjList.get(i).add(j);
                }
            }
        }

        // 모든 노드에 대해 DFS 수행
        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                dfs(i);
                answer++;
            }
        }

        return answer;
    }

    private void dfs(int node) {
        visited[node] = true;
        for (int neighbor : adjList.get(node)) {
            if (!visited[neighbor]) {
                dfs(neighbor);
            }
        }
    }
}

Stack 자료구조 사용해서 구현

public class DFS {
    public static void dfs(List<List<Integer>> graph, int startNode) {
        int n = graph.size();
        // 방문처리에 사용 할 배열선언
        boolean[] visited = new boolean[n];
        // DFS 사용 할 스택
        Stack<Integer> stack = new Stack<>();
        int[] depth = new int[n];

		// 시작 노드를 스택에 넣어줍니다.
        stack.push(startNode);
        depth[startNode] = 0;

        // 스택이 비어있지 않으면 계속 반복
        while (!stack.isEmpty()) {
        	// 스택에서 하나를 꺼냅니다.
            int node = stack.pop();

			// 노드를 방문하지 않았을 경우에 방문처리
            if (!visited[node]) {
                visited[node] = true;
                System.out.println("Visiting node " + node + " at depth " + depth[node]);

				// 꺼낸 노드와 인접한 노드 찾기
                for (int neighbor : graph.get(node)) {
                	// 인접한 노드를 방문하지 않았을 경우에 스택에 넣습니다. 
                    if (!visited[neighbor]) {
                        stack.push(neighbor);
                        depth[neighbor] = depth[node] + 1;
                    }
                }
            }
        }
    }

    public static void main(String[] args) {
        int n = 7; // 노드의 개수
        List<List<Integer>> graph = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            graph.add(new ArrayList<>());
        }

        // 그래프 초기화
        graph.get(0).add(1);
        graph.get(0).add(2);
        graph.get(1).add(0);
        graph.get(1).add(3);
        graph.get(1).add(4);
        graph.get(2).add(0);
        graph.get(2).add(5);
        graph.get(2).add(6);
        graph.get(3).add(1);
        graph.get(4).add(1);
        graph.get(5).add(2);
        graph.get(6).add(2);

        dfs(graph, 0);
    }
}

출력결과

Visiting node 0 at depth 0
Visiting node 2 at depth 1
Visiting node 6 at depth 2
Visiting node 5 at depth 2
Visiting node 1 at depth 1
Visiting node 4 at depth 2
Visiting node 3 at depth 2

BFS( 너비 우선 탐색 , Bread-First Search)

루트 노드(혹은 다른 임의의 노드)에서 시작한 인접 노드를 먼저 탐색하는 방법

특징

• BFS는 재귀적으로 동작하지 않습니다.
• 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야한다는 것입니다. (이를 검사하지 않을 경우 무한루프에 빠질 수 있다. )
• BFS는 방문한 노드들을 차례로 저장한 후 꺼낼 수 있는 자료 구조인 큐를 사용합니다.
  • 즉, 선입선출 원칙으로 탐색합니다.
• 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법입니다.
• 깊게(deep) 탐색하기 전에 넓게(wide) 탐색하는 것입니다.
• 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 이 방법을 사용합니다.

Java로 BFS 구현

예시 문제
https://school.programmers.co.kr/learn/courses/30/lessons/1844

class Solution {
	// 상하좌우 이동을 위한 방향 배열
    int[] dx = { -1, 1, 0, 0 };
    int[] dy = { 0, 0, -1, 1 };

    public int solution(int[][] maps) {
        int n = maps.length;
        int m = maps[0].length;
         // 방문 여부를 나타내는 배열
        boolean[][] visited = new boolean[n][m];
        Queue<Node> queue = new LinkedList<>();

		// 시작 지점을 큐에 넣음
        queue.offer(new Node(0, 0, 1));

        while (!queue.isEmpty()) {
            Node currentNode = queue.poll();
            int x = currentNode.x;
            int y = currentNode.y;
            int depth = currentNode.depth;
            
             // 도착 지점에 도달한 경우 최단 거리를 반환
            if (x == n - 1 && y == m - 1) {
                return depth;
            }

			// 상하좌우로 이동
            for (int i = 0; i < 4; i++) {
                int newX = x + dx[i];
                int newY = y + dy[i];

				// 유효한 범위 내에 있고, 벽이 아니며 아직 방문하지 않은 경우
                if (newX >= 0 && newX < n && newY >= 0 && newY < m && !visited[newX][newY] && maps[newX][newY] == 1) {
                    visited[newX][newY] = true;
                    // 다음 위치를 큐에 추가
                    queue.offer(new Node(newX, newY, depth + 1));
                }
            }
            
        }

        return -1;
    }

    private class Node {
        int x;
        int y;
        int depth;

        public Node(int x, int y, int depth) {
            this.x = x;
            this.y = y;
            this.depth = depth;
        } 
    }
}

출력결과

maps															answer
[[1,0,1,1,1],[1,0,1,0,1],[1,0,1,1,1],[1,1,1,0,1],[0,0,0,0,1]]	11

깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS) 활용한 문제 유형/응용

DFS, BFS은 특징에 따라 사용에 더 적합한 문제 유형들이 있습니다.

1. 그래프의 모든 정점을 방문하는 것이 주요한 문제

   단순히 모든 정점을 방문하는 것이 중요한 문제의 경우 DFS, BFS 두 가지 방법 중 어느 것을 사용하셔도 상관없습니다.

2. 경로의 특징을 저장해둬야 하는 문제

   예를 들면 각 정점에 숫자가 적혀있고 a부터 b까지 가는 경로를 구하는데 경로에 같은 숫자가 있으면 안 된다는 문제 등, 각각의 경로마다 특징을 저장해둬야 할 때는 DFS를 사용합니다. (BFS는 경로의 특징을 가지지 못합니다)

3. 최단거리 구해야 하는 문제

   미로 찾기 등 최단거리를 구해야 할 경우, BFS가 유리합니다.
   왜냐하면 깊이 우선 탐색으로 경로를 검색할 경우 처음으로 발견되는 해답이 최단거리가 아닐 수 있지만,
   너비 우선 탐색으로 현재 노드에서 가까운 곳부터 찾기 때문에경로를 탐색 시 먼저 찾아지는 해답이 곧 최단거리기 때문입니다.

이밖에도

• 검색 대상 그래프가 정말 크다면 DFS를 고려
• 검색대상의 규모가 크지 않고, 검색 시작 지점으로부터 원하는 대상이 별로 멀지 않다면 BFS 사용

출처 : https://namu.wiki/w/%EB%84%88%EB%B9%84%20%EC%9A%B0%EC%84%A0%20%ED%83%90%EC%83%89,
https://bbangson.tistory.com/42,
https://codingnojam.tistory.com