이분 탐색 / 이진 탐색 (Binary Search)

정렬된 배열 또는 리스트에 적합한 고속 탐색 방법이다.

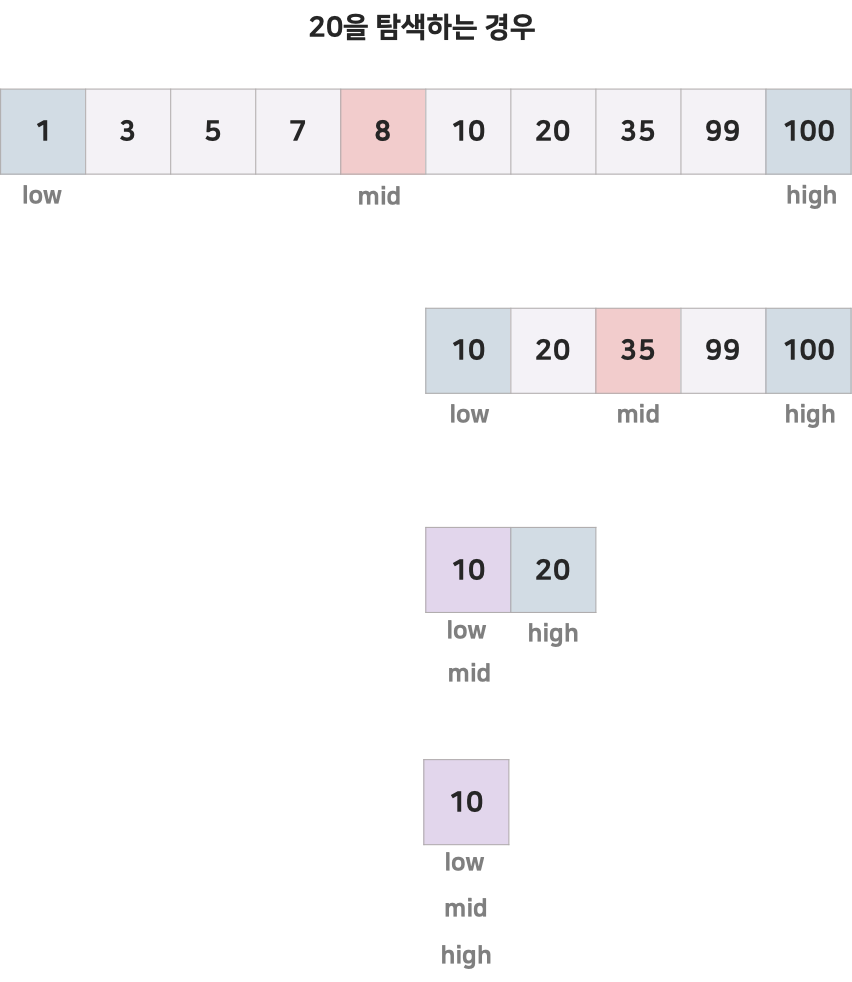
• 배열의 중앙에 있는 값을 조사하여 찾고자 하는 항목이 왼쪽 또는 오른쪽 부분 배열에 있는지를 알아내어 탐색의 범위를 반으로 줄인다.
• 찾고자 하는 값이 속해있지 않은 부분은 전혀 고려할 필요가 없기 때문에, 매 단계에서 검색해야 할 리스트의 크기를 반으로 줄일 수 있다.
• 이러한 방법을 반복적으로 사용해 탐색하는 방법이 이진 탐색이다.
• 데이터의 삽입이나 삭제가 빈번할 시에는 적합하지 않고, 주로 고정된 데이터에 대한 탐색에 적합하다.

---

탐색법

1. 처음 범위는 인덱스 0부터 끝까지이다. 이 때 중간 인덱스를 mid로 한다.(이 때 배열 / 리스트는 정렬되어 있어야한다.)

2. mid의 값와 찾는 원소를 비교한다.
   2-1. 찾는 원소와 mid의 값이 같다면 탐색 종료한다.
   2-2. mid의 값 < 찾는 원소 일 때 left는 mid + 1로 하여 2)를 다시 반복한다.
   2-3. mid의 값 > 찾는 원소 일 때 right는 mid - 1 로 하여 2)를 다시 반복한다.

3. 만약 right > left가 된다면 해당 배열에 찾는 원소가 없는 것이다.

---

재귀로 구현

int binarySearch1(int key, int low, int high) {
	int mid;

	if(low < high) {
		mid = (low + high) / 2;

		if(key == arr[mid]) { // 탐색 성공 
			return mid;
		} else if(key < arr[mid]) {
			// 왼쪽 부분 arr[0]부터 arr[mid-1]에서의 탐색 
			return binarySearch1(key ,low, mid);  
		} else {
			// 오른쪽 부분 - arr[mid+1]부터 arr[high]에서의 탐색 
			return binarySearch1(key, mid+1, high); 
		}
	}

	return -1; // 탐색 실패 
}

---

반복문으로 구현

int binarySearch2(int key, int low, int high) {
	int mid;

	while(low < high) {
		mid = (low + high) / 2;

		if(key == arr[mid]) {
			return mid;
		} else if(key < arr[mid]) {
			high = mid;
		} else {
			low = mid + 1;
		}
	}

	return -1; // 탐색 실패 
}

---

시간복잡도

순차적 탐색	이분 탐색
O(n)	O(log n)

참고 : https://minhamina.tistory.com/127