플로이드-워셜 알고리즘 (Floyd-Warshall)

a·2024년 1월 2일

알고리즘 플로이드 워셜

알고리즘

목록 보기

12/17

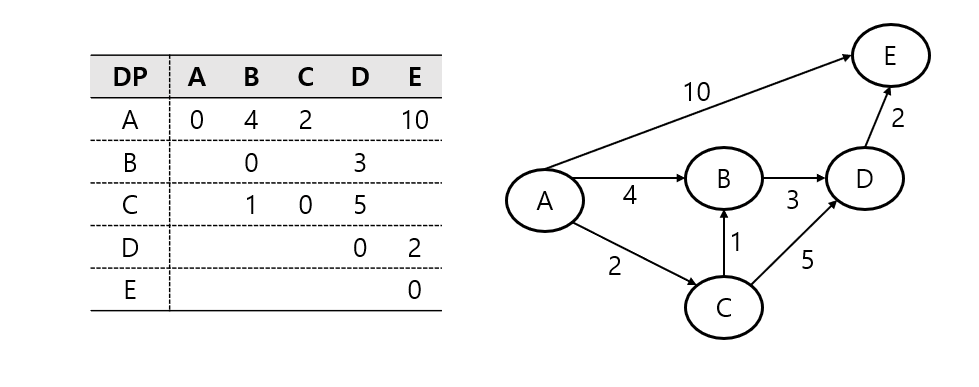
Floyd-Warshall 알고리즘 이란?

모든 노드간에 최단거리를 구하는 알고리즘
다익스트라, 벨만포드는 한 노드에서 모든노드까지의 최단경로
Floyd-Warshall은 모든노드에서 모든노드까지의 최단 경로
벨만포드와 같이 가중치에 음수가 있어도 가능
음수 순환 사이클이 없는 그래프에서, 모든 점에서 모든 점까지의 최단거리를 구하는 알고리즘
시간복잡도 : O(N³) (N:노드의 수)

시간복잡도
각 중간 정점 k에 대해 모든 i, j 쌍에 대해 계산하여, 3중 for문을 통해 모든 경우의 수를 비교하기에 총 n∗n∗n=n³회 계산이 이루어지고, 각 계산은 O(1) 시간 걸린다.
따라서 시간복잡도는 O(n³)이다.

플로이드-워셜 알고리즘이 DP인 이유
최적 부분 구조로 작은 문제를 해결하고, 중복된 부분 문제를 반복적으로 계산하지 않고, 메모이제이션을 통해 이전 결과를 재사용함에 있다.

플로이드 워셜 탐색과정

DP 2차원 배열을 각 정점 사이의 가중치로 초기화한다. 가중치가 없는 경우 INF (Integer.MAX_VALUE)로 설정한다.
각 중간 정점 k에 대하여 시작 정점 i와 끝 정점 j의 가능한 모든 조합을 반복문으로 탐색한다.
(현재 거리 > 중간 정점 k를 거친 거리 ) D[i][j] = min(D[i][k] + D[k][j], D[i][j])이면 DP를 업데이트한다.
그래프의 모든 정점에 대해 2- 3단계를 반복한다.

동작 예

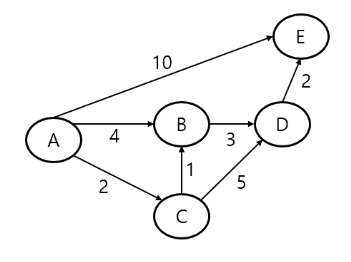
2차원 인접행렬을 구성한다.
이 때는 자기 자신을 가는 경우 뿐이니 자기 자신에 가중치 0을 대입한다.

	A	B	C	D	E
A	0	∞	∞	∞	∞
B	∞	0	∞	∞	∞
C	∞	∞	0	∞	∞
D	∞	∞	∞	0	∞
E	∞	∞	∞	∞	0

주어진 그래프의 간선 정보를 바탕으로 초기 인접 행렬을 생성하면 다음과 같다.
여기서 ∞는 두 정점 사이에 직접적인 경로가 없음을 나타낸다.

	A	B	C	D	E
A	0	4	2	∞	10
B	∞	0	∞	3	∞
C	∞	1	0	5	∞
D	∞	∞	∞	0	2
E	∞	∞	∞	∞	0

플로이드 워셜 알고리즘을 적용하여 최단 거리 행렬을 계산하면 다음과 같다.

	A	B	C	D	E
A	0	3	2	6	8
B	∞	0	∞	3	5
C	∞	1	0	4	6
D	∞	∞	∞	0	2
E	∞	∞	∞	∞	0

이 행렬에서 정점 A에서 정점 E까지의 최단 거리인 A -> C -> B -> D -> E로 8을 나타낸다.

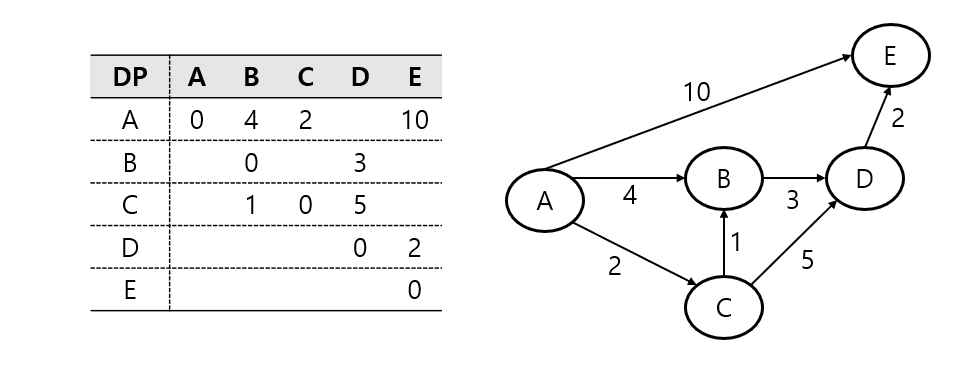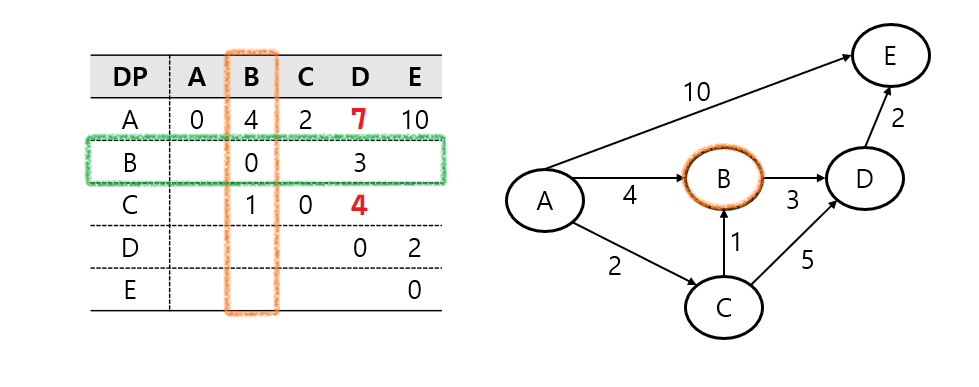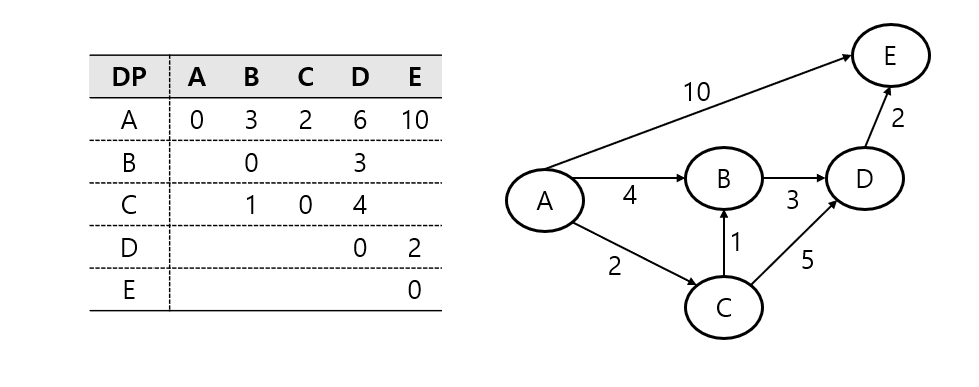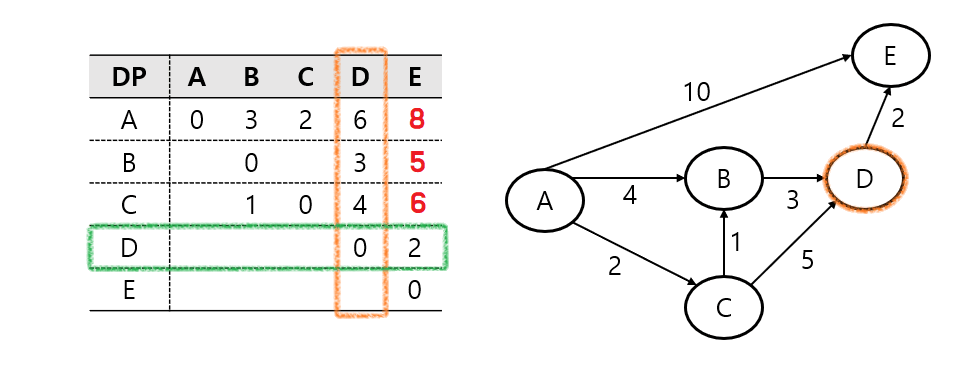
플로이드 워셜 알고리즘은 모든 정점 쌍의 최단 경로 찾기를 목표로 하며, INF 값이 사라지지 않더라도 다른 모든 정점을 거치는 경우를 고려한 후에 종료되는 알고리즘임을 알 수 있음.

플로이드 워셜 장단점

플로이드 워셜 장점:

Dijkstra의 알고리즘과 달리 가중치가 음수여도 처리할 수 있다.
방향 그래프와 무방향 그래프 모두에서 작동한다.
구현하고 이해하는 것이 매우 간단하다.

플로이드 워셜 단점:

시간 복잡도는 O(n³)이므로 큰 그래프의 경우 속도가 느려진다.
중간 결과를 저장하려면 많은 양의 메모리를 필요로 한다.
가중치의 합이 음수인 사이클을 갖는 그래프에서는 작동하지 않는다.

플로이드 워셜 알고리즘 자바 구현

https://www.acmicpc.net/problem/11404
위 문제 풀이 방식입니다.

public class FloydWarshall {
    public static void main(String[] args) throws IOException {
    Scanner sc = new Scanner(System.in);
    int n = sc.nextInt();
    int m = sc.nextInt();

    int[][] graph = new int[n + 1][n + 1];

    for (int i = 1; i <= n; i++) {
        Arrays.fill(graph[i], Integer.MAX_VALUE);
        graph[i][i] = 0;
    }

    for (int i = 0; i < m; i++) {
        int a = sc.nextInt();
        int b = sc.nextInt();
        int c = sc.nextInt();
        
        if (graph[a][b] > c) {
          graph[a][b] = c;
        }
    }

      for (int k = 1; k <= n; k++) {  // 경유 노드 확인
            for (int i = 1; i <= n; i++) {  // 출발지
                if (i == k) continue;  // 출발지와 경유지가 같으면 다음 탐색
                for (int j = 1; j <= n; j++) {  // 도착지
                    if (j == i || j == k) continue;  // 출발지와 도착지가 같거나 도착지가 경유지이면 다음 탐색
                    if (graph[i][k] != Integer.MAX_VALUE && graph[k][j] != Integer.MAX_VALUE) { // 오버플로우가 발생하여 음수가 될 수 있다 
                    graph[i][j] = Math.min(graph[i][k] + graph[k][j], graph[i][j]);  // 경유하거나 직접가거나 더 짧은 경로로 대체
                }
            }
        }
        

        for(int i = 1 ; i <= n ; i ++) {
            for(int j = 1 ; j <= n ; j ++) {
                if(graph[i][j] == Integer.MAX_VALUE) {
                    System.out.print(0 + " ");
                } else {
                    System.out.print(graph[i][j] + " ");
                }
            }
            System.out.println();
        }
    }
}

플로이드-워셜 알고리즘은 주로 최단 경로를 찾는 데 사용되지만, 그래프의 모든 노드 간의 관계를 탐색하는 데 매우 유용합니다. 선수 간의 승리 관계와 같이 이진 관계(이기는 경우와 지는 경우)를 다루는 데 적합합니다.

class Solution {
    public int solution(int n, int[][] results) {
        int answer = 0;
        int[][] graph = new int[n + 1][n + 1];

        for (int[] result : results) {
            graph[result[0]][result[1]] = 1;
            graph[result[1]][result[0]] = -1;
        }

        for (int k = 1; k <= n; k++) {
            for (int i = 1; i <= n; i++) {
                if (i == k) continue;
                for (int j = 1; j <= n; j++) {
                    if (j == k || j == i) continue;
                    if (graph[i][k] == 1 && graph[k][j] == 1) {
                        graph[i][j] = 1; 
                        graph[j][i] = -1;
                    }
                }
            }
        }

        for (int i = 1; i <= n; i++) {
            int cnt = 0;
            for (int j = 1; j <= n; j++) {
                if (graph[i][j] != 0) {
                    cnt++;
                }
            }
            if (cnt == n - 1) {
                answer++;
            }
        }
        return answer;
    }
}

플로이드-워셜 알고리즘 사용

모든 정점 쌍의 최단 거리를 필요로 하는 상황
음의 가중치를 가진 간선이 있는 경우
밀집 그래프 처리

시간 복잡도는 O(V^3)으로, 정점의 수가 많은 밀집 그래프에서는 계산 시간이 많이 걸립니다. 하지만, 간선의 수가 많은 밀집 그래프에서는 다른 알고리즘(예: 다익스트라)보다 효율적
데이터 분석 및 네트워크 최적화 등에서 효율적으로 사용

인접 행렬 vs 인접 리스트

플로이드-워셜 알고리즘은 주로 인접 행렬을 사용하여 구현한다. 각 정점 쌍에 대해 다른 모든 정점을 거쳐 가는 경우를 고려하므로, 인접 행렬이 이러한 연산을 수행하기 더 편리하다.

인접 행렬

각 정점 쌍의 거리를 쉽게 참조하거나 업데이트할 수 있다.
행렬의 행과 열은 각각 시작 정점과 도착 정점을 나타내며, 각 셀의 값은 해당 정점 쌍의 거리를 나타낸다.

인접 리스트

그래프의 간선 정보를 리스트로 저장하는데, 특정 정점에서 직접 연결된 정점들을 찾는 데 유용하다.
즉, "정점 A에서 어디로 갈 수 있나요?"라는 질문에 쉽게 답할 수 있다.
따라서, 모든 정점 쌍에 대해 계산을 수행해야 하는 플로이드-워셜 알고리즘에는 덜 적합하다.

결론적으로, 플로이드-워셜 알고리즘은 인접 행렬을 사용하여 구현하는 것이 일반적이다.

참고
https://olrlobt.tistory.com/43
https://chb2005.tistory.com/80
https://velog.io/@jhno96/JAVA-%ED%94%8C%EB%A1%9C%EC%9D%B4%EB%93%9C-%EC%99%80%EC%83%AC-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98