python Data Structure-Tree 트리

BackEnd_Ash.log·2020년 7월 30일

python data Structure tree

알고리즘

목록 보기

7/14

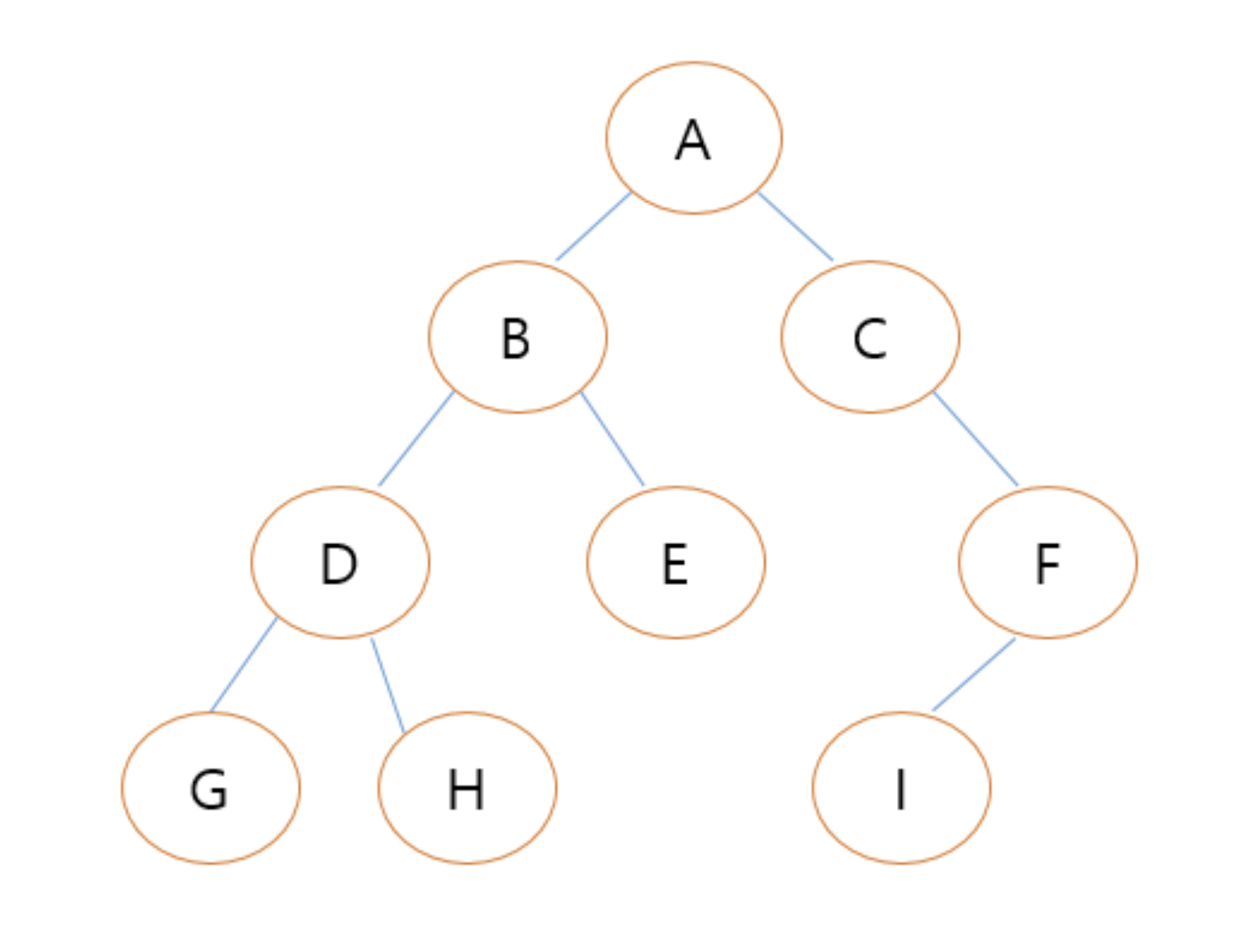
📌트리 ??

하나의 뿌리에서 위로 뻗어 나가는 형상처럼 생겼다
트리는 자식도 트리고 또 그 자식도 트리다.

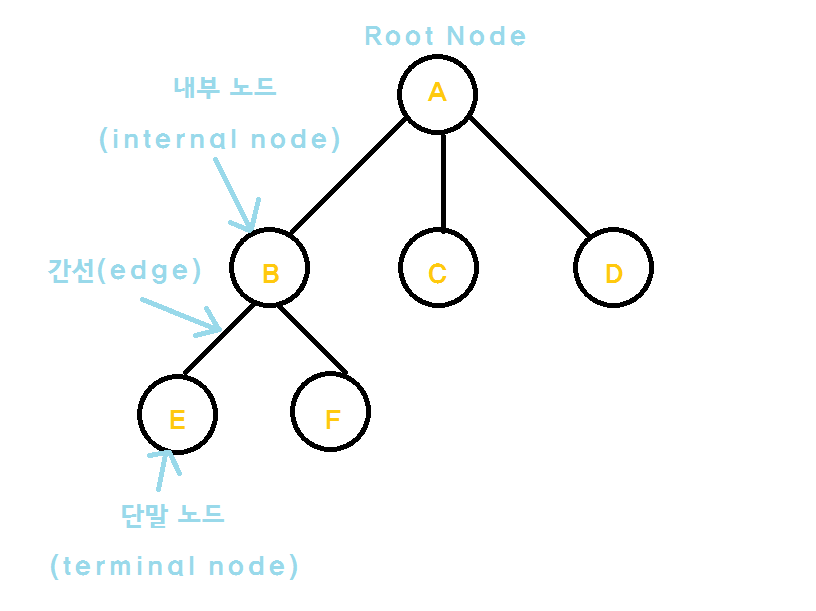
👉트리의 명칭

트리는 항상 루트(root) 에서부터 시작된다.
루트는 자식 노드를 가지며 , 간선(Edge) 으로 연결되어 있다.
자식 노드의 개수는 차수 라고 한다.
크기는 자신을 포함한 모든 자식 노드의 개수다.
높이는 현재 위치에서부터 리프까지의 거리 , 깊이는 루트에서부터 현재 노드까지의 거리이다.

👉그래프 vs 트리

트리는 순환 구조를 갖지 않는 그래프이다

핵심은 순환 구조가 아니라는 데 있다.

트리는 특수한 형태의 그래프의 일종이다.

크게 그래프의 범주에 포함이 된다.

트리는 그래프와 달리 어떠한 경우에도 한번 연결된 노드가 다시 연결되는 법이 없다.

👉Binary Tree

트리 자료구조는 이진 트리 와 이진 탐색트리 이다.

이진 트리는 한 노드가 자식 노드를 두 개 이하만 갖는 트리 입니다.

이진 트리의 노드도 데이터부분과 참조 부분으로 이루어져 있습니다.

다만 참조가 두개 입니다.

왼쪽 자식 노드를 가리키는 참조와 오른쪽 자식 노드를 가리키는 참조입니다.

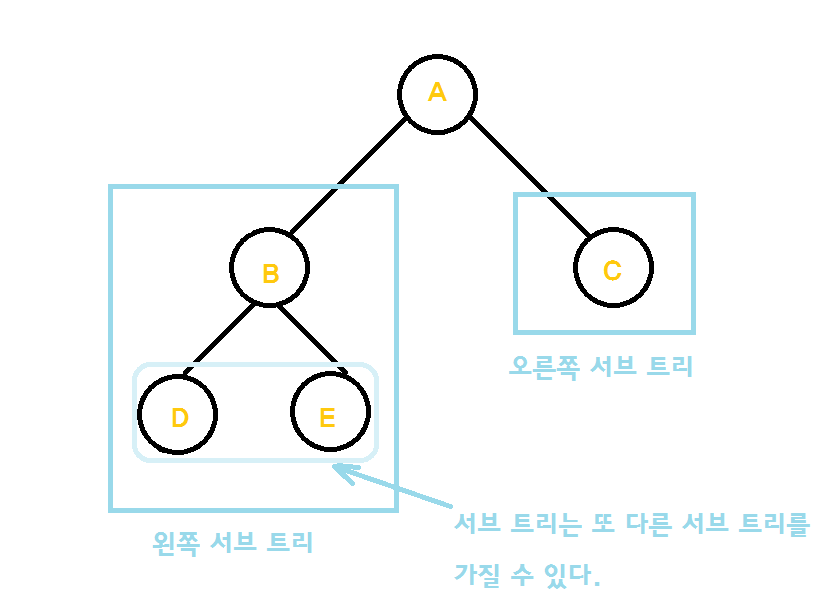
정 이진 트리 ( Full Binary Tree )

정 이진트리는 모든 노드가 0 개 또는 2개의 자식 노드를 갖는다.

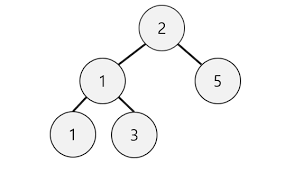
완전 이진 트리 ( Complete Binary Tree )

완전 이진 트리는 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며 , 마지막 레벨의 모든 노드는 가장 왼쪽부터 채워져 있다.

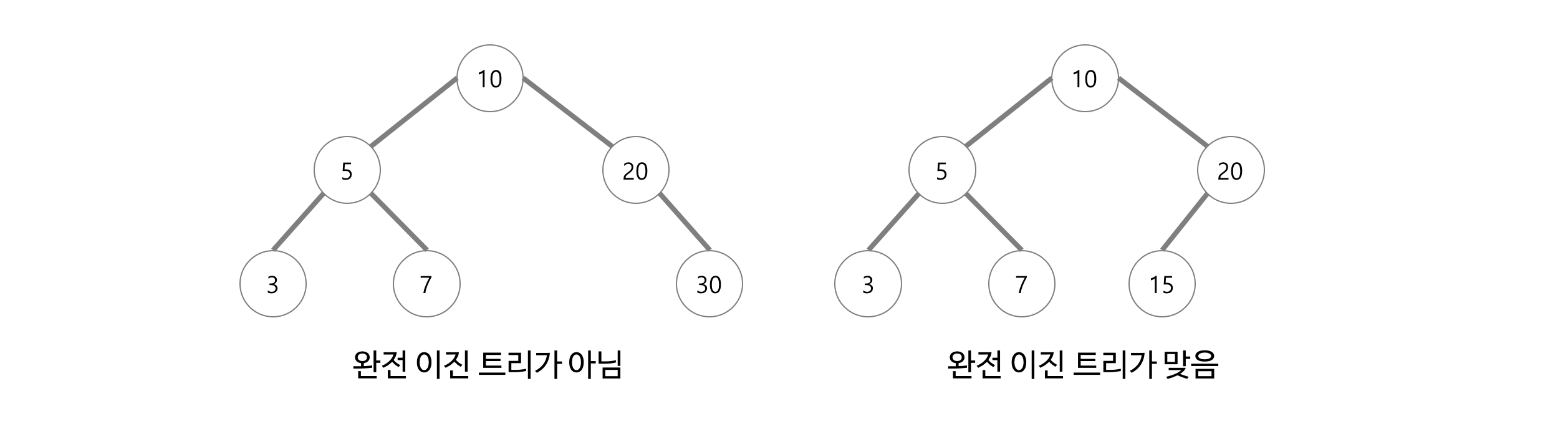
포화 이진 트리 ( Perfect Binary Tree )

포화 이진트리는 모든 노드가 2개의 잣기노드를 갖고있으며 , 모든 리프 노드가 동일한 깊이 또는 레벨을 갖는다.문자 그대로 , 가장 완벽한 유형의 트리다.

👉Non-Binary Tree

대표적인 사용처는 trie 자료구조이다.
trie 는 컴퓨터에서 검색을 뜻하는 retrieval 에서 온 단어이다.

Prefix tree 라고도 하는데 직관적이고 부르기도 쉬워서 이렇게 부르는 사람도 꽤 있다.

Trie 에서 어떤 문자열을 검색할 때의 시간 복잡도는 O(m) 밖에 안된다.
그래서 다른 자료구조에 비해 문자열을 검색하는데 특화된 자료구조임을 알 수 있다.

📌트리 노드 구현

이진 트리를 구현하려면 먼저 그 재료가 되는
Node 클래스를 정의해야 한다.

트리 노드 클래스는 멤버가 세 개입니다.

데이터를 담는 data
왼쪽 자식노드를 가리키는 left
오른쪽 자식노드를 가리키는 right

class Node:

    def __init__(self, data):
        self.left = None
        self.right = None
        self.data = data

    def PrintTree(self):
        print(self.data)  # 10


root = Node(10)
root.PrintTree()

트리에 삽입하려면 위에서 만든 동일한 노드 클래스를 사용하고 트리에 삽입 클래스를 추가해야한다.
삽입 함수는 노드의 값을 상위 노드(부모 노드)와 비교하고 이를 왼쪽 노드 또는 오른쪽 노드로 추가하기로 결정한다. 마지막으로 PrintTree 함수를 사용하여 트리를 출력한다.

class Node:

    def __init__(self, data):

        self.left = None
        self.right = None
        self.data = data

    def insert(self, data):
        # Compare the new value with the parent node
        if self.data:
            if data < self.data:
                if self.left is None:
                    self.left = Node(data)
                else:
                    self.left.insert(data)
            elif data > self.data:
                if self.right is None:
                    self.right = Node(data)
                else:
                    self.right.insert(data)
        else:
            self.data = data

    # Print the tree
    def PrintTree(self):
        if self.left:
            self.left.PrintTree()
        print(self.data),
        if self.right:
            self.right.PrintTree()


# Use the insert method to add nodes
root = Node(12)
root.insert(6)
root.insert(14)
root.insert(3)

root.PrintTree()