[알고리즘] 동적계획법 (Dynamic Programming, DP)

"한번 계산한 문제는 다신 계산하지 않도록 한다!!"

👑 DP 개념: "기억하며 풀기"

-> 큰 문제를 작은 문제로 쪼개서 그 답을 저장해두고 재활용
(* 했던 계산을 또 하는 그러한 번거로움을 해결해줌)

-> 동적 계획법으로 구할 수 있는 것은 백트랙킹, 재귀로도 구할 수 있음. BUT, 백트랙킹은 모든 경우의 수를 검사하므로 동적계획법이 더 빠름.

👑 분할 정복과의 차이점

-> 주어진 문제를 하위 문제로 해결하고, 연계적으로 큰 문제를 해결한다는 공통점
BUT,

• 분할 정복: 하위 문제가 동일하게 중복되지 않는 경우
• DP: 하위 문제가 동일하게 중복되는 경우

ex>

• 병합정렬 (분할 정복): 작은 하위 문제로 쪼개지지만, 중복되는 하위 문제가 발생하지 않음
• 피보나치 (DP): 중복적인 하위 문제가 발생 함

👑 DP의 사용 조건

1. 겹치는 부분 문제 (Overlapping subproblems)
   : 동일한 작은 문제들이 반복하여 나타나야 함

2. 최적 부분 구조 (Optimal substructure)
   : 부분 문제의 최적 결괏값을 사용해, 전체 문제의 최적 결괏값을 낼 수 있어야 함

👑 DP 사용하기

1) DP로 풀 수 있는 문제인지 확인: 위의 두 조건 확인 (작은 문제들이 반복하여 나타나는 지, 부분 최적값을 전체 최적 값을 구할 때 사용할 수 있는지)
2) 문제의 변수 파악: 현재 변수에 따라 그거에 따른 결괏값을 구하고 재사용하게 되는 것이다.
3) 변수 간 관계식 만들기(점화식): 피보나치 수열에서는 f(n) = f(n-1) + f(n-2)
4) 메모하기(memoization or tabulation): 배열을 만들어, 작은 문제의 결괏값을 저장한다.
5) 기저 상태 파악하기: 가장 작은 문제의 상태를 파악한다.
6) 구현하기:

• bottom-up: 반복문
• top-down: 재귀

👑 DP 파이썬 구현

-> 분할정복 알고리즘과 비슷!
1. bottom-up: 반복문
:재귀아래에서 부터 계산을 수행 하고 누적시켜서 전체 큰 문제를 해결하는 방식
-> dp라는 배열을 만들고, dp[0]부터 시작해서 반복문으로 결괏값을 내고, 목표값인 dp[n]까지 전이시켜 사용
-> 수열과 같이 연속적이지 않은 자료가 주어졌을 때 유용

2. top-down: 재귀(메모제이션 기법)
   : dp[n]인 맨 위에서 부터 호출을 시작하여, dp[0]까지 도달한 후, 재귀를 통해 전이시켜 재활용하는 방식

-> 즉, bottom-up은 맨 아래값부터 값을 위로 전이시키며 차근차근 올라오는 거고, top-down은 무작정 목푯값부터 아래로 내려가면서, 재귀로 전이시키는 것
-> 2가지 방법으로 모두 풀 수 있는 문제가 있고, 한 가지 방법으로만 풀 수 있는 문제가 있음!! : dp문제를 많이 풀어보며, 경험적으로 알 수 있음

👑 DP 문제 예시

피보나치 수열

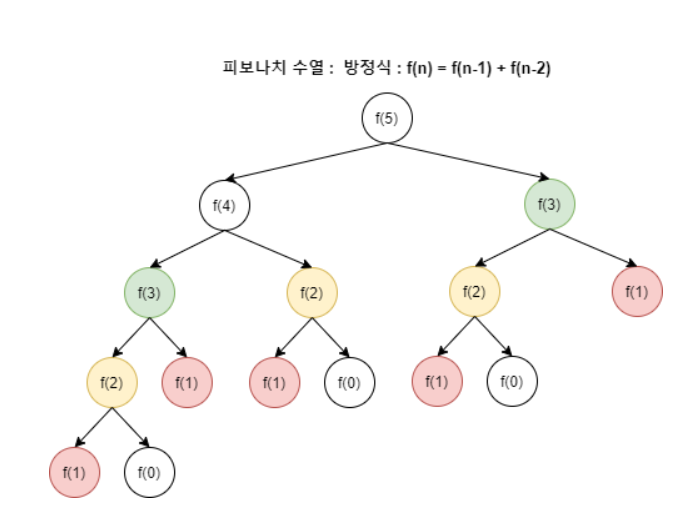
-> 재귀로 피보나치를 구현하는 경우, 같은 함수를 호출해야하는 경우의 수가 많아진다. -> 비효율적
--> 작은 문제의 결괏값을 저장해두었다가 재활용하자!

1. bottom-up 방식: 반복문
   

2. top-down 방식: 재귀- 메모제이션
   
   -> 메모제이션 기법(top-down: 재귀) 으로 피보나치 수열 구현함

------> 주로 bottom-up방식, 즉 반복문으로 해결하도록 하자!

⭕ 정리:
동적계획법은 작은 문제로 쪼개서 그 결괏값을 저정해서 재활용하기 위한 것이다. 분할정복과 헷갈릴 수 있다. 둘 다 하위 문제로 쪼갠다는 것은 같지만 동적계획법은 하위 문제가 중복적으로 반복되야 하고, 하위 문제의 최적값이 전체 결괏값의 최적값에 적용이 되어야 한다는 특징이 있다. 동적계획법 문제의 대표적인 예시는 피보나치 수열이다. 단지, 재귀로 풀 때에는 같은 함수를 여러 번 호출해야하기 때문에, 시간 복잡도나 공간복잡도 측면에서 비효율적이다.
동적계획법을 구현할 수 있는 방법은 2가지가 있다. 첫 번째는 bottom-up 방식으로 반복문을 통해 구현할 수 있는데, 수열과 같이 비연속적인 숫자들이 주어졌을 때 유용하다. dp[0]의 값부터 시작해서 값들을 전이시켜 가며 dp[n]까지 도달하는 것이다. 두 번째는 top-down 방식인데, 재귀를 통해 해결할 수 있다. 이는 dp[n]부터 시작한다. dp[0]까지 내려가서 값을 전이시켜 재활용하게 된다. 저장된 값을 메모리에서 가져와서 쓴다고 하여, 메모제이션 기법이라고도 한다.