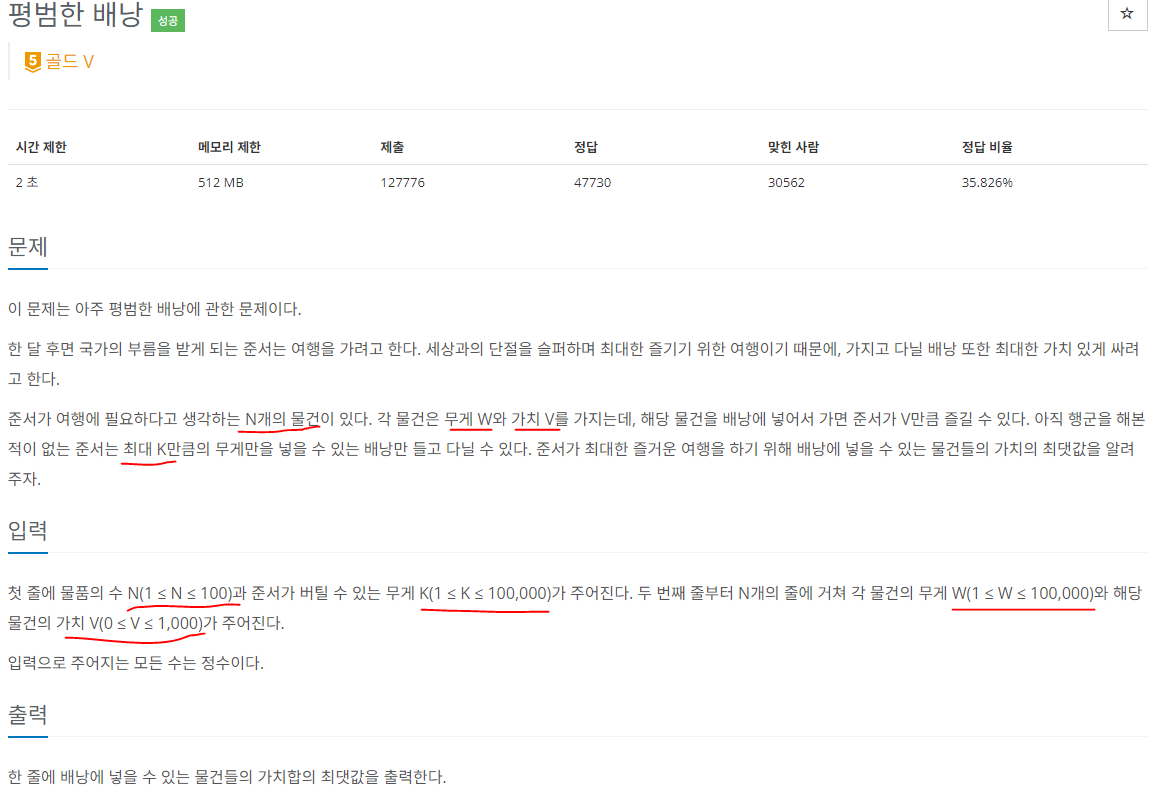
풀이

1차 시도(부분 집합)

처음엔 부분집합으로 시도를 하려고 했다
하지만 부분집합은 2^n
n = 100
2^100 =
절대 불가능 하다

2차 시도(그리디)

무게당 가격이 가장 비싼걸 넣어주려고 생각했다.
입력이
(6,13), (4,8), (3,6), (5,12)
무게 / 가격은 각각
2.17 2 2 2.4

(5.12)를 가장 먼저 넣어주게 되는데

이렇게 되면 얻는 이익은 12가 된다
하지만 (4,8), (3,6)을 넣으면 이익이 14로 답이 틀리다
이렇게 무게 당 가격이 가장 비싼걸 넣어주는 경우는 물건을 쪼개서 넣어주는 경우에 이 방법을 사용 할 수 있다.
이 방법은 Fractional Knapsack이라고 한다.

3차 시도(DP)

DP 조건

1. 최적 부분 구조(Optimal substructure)

   큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제 해결

2. 중복되는 부분 문제(Overlapping Subproblem)

   동일한 작은 문제를 반복적으로 해결

풀이

동일하게 (6,13), (4,8), (3,6), (5,12) 입력이 들어온다고 했을 때

이런 DP 테이블을 만들수 있다.
DP 테이블을 만드는 방법은 2가지다
그 상황에서 무게에 여유가 있어 물건을 선택하는 경우와, 물건을 선택하지 않는 경우

물건을 선택하지 않는 경우엔 이전 값을 그대로 사용하고
물건을 선택하는 경우엔 이전값과, 물건을 선택했을 때의 값을 비교해서 최대 값을 DP 테이블에 적어둔다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		
		int n = Integer.parseInt(st.nextToken()); // 물 품수
		int k = Integer.parseInt(st.nextToken()); // 최대 무게
		
		int [] w = new int[n+1];// 무게 담아줄 배열
		int [] v = new int[n+1]; // 가격 담아줄 배열
		int [][] dp = new int[n+1][k+1];
		
		for(int i = 1; i <=n; i++) {
			StringTokenizer str = new StringTokenizer(br.readLine());
			w[i] = Integer.parseInt(str.nextToken());
			v[i] = Integer.parseInt(str.nextToken());
		}
		for(int i = 1; i <=n; i++) {
			for(int j = 1; j<=k; j++) {
				//무게를 안 담을 경우
				if(w[i] > j) { // j: 해당 열에서 담 을 수 있는 최대 값 
					dp[i][j] = dp[i-1][j]; // 이전 값 넣어줌
				}
				else { //무게를 담을 경우
					// 이전값이랑 값을 담은 값중 최대값 을 넣어줌
					// 담았으니까 v[i] 담은 현재 값 + 아직 담 을 수 있는 무게가 남았네?
					// 그럼 그 무게 값 더해 줌 j - w[i] 
					dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j - w[i]] + v[i]); 
				}
			}
		}
		System.out.println(dp[n][k]);
	}
}