[알고리즘] 그래프

이상현·2020년 12월 1일
0

알고리즘_강의노트

목록 보기
8/8
post-thumbnail

그래프

정의

  • 현상이나 사물을 정점vertex과 간선edge으로 표현한 것
  • Graph G = (V, E)
    • V : 정점 집합
    • E : 간선 집합
  • 두 정점이 간선으로 연결되어 있으면 인접adjacent하다고 한다.
    • 간선은 두 정점의 관계를 나타낸다.

그래프의 예

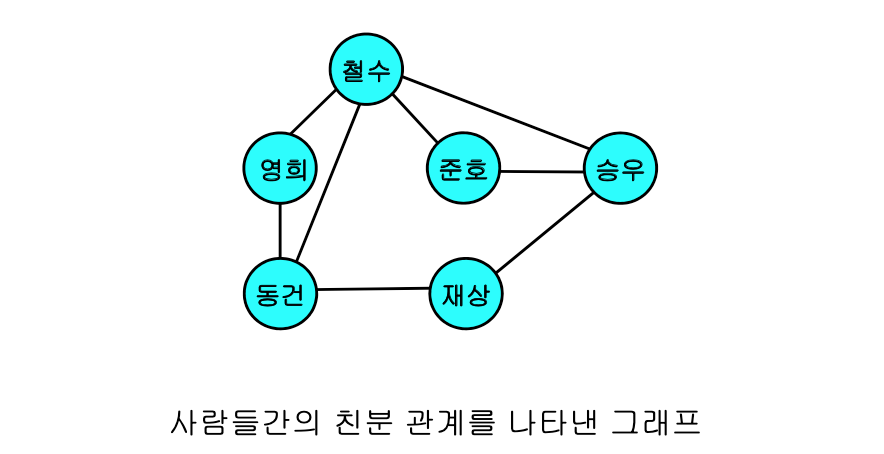
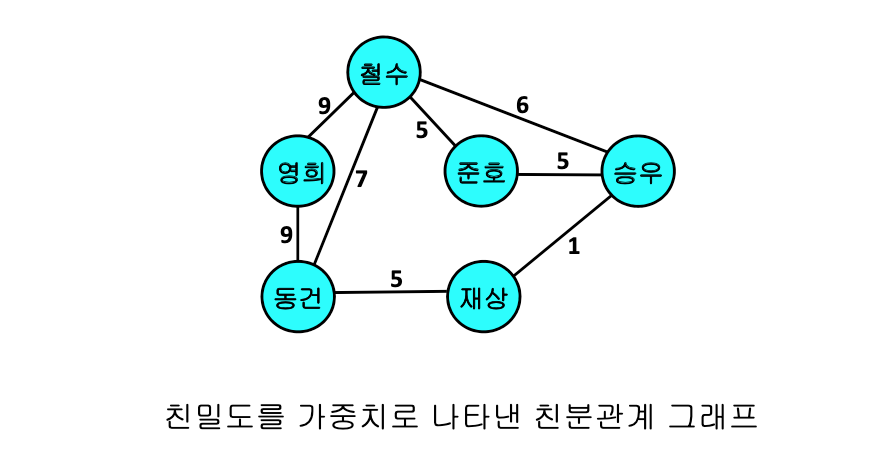
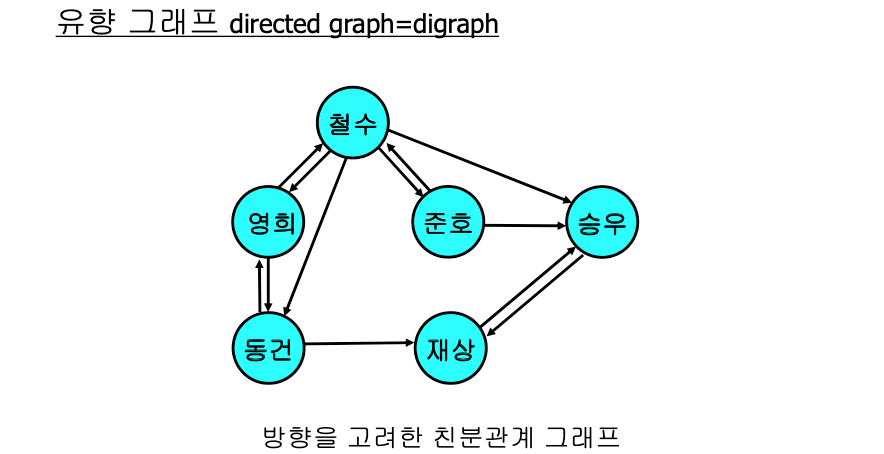
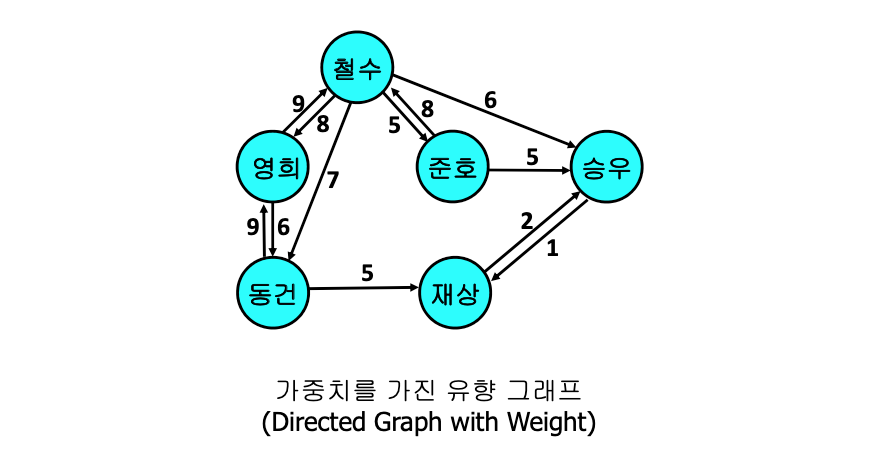
그래프의 표현

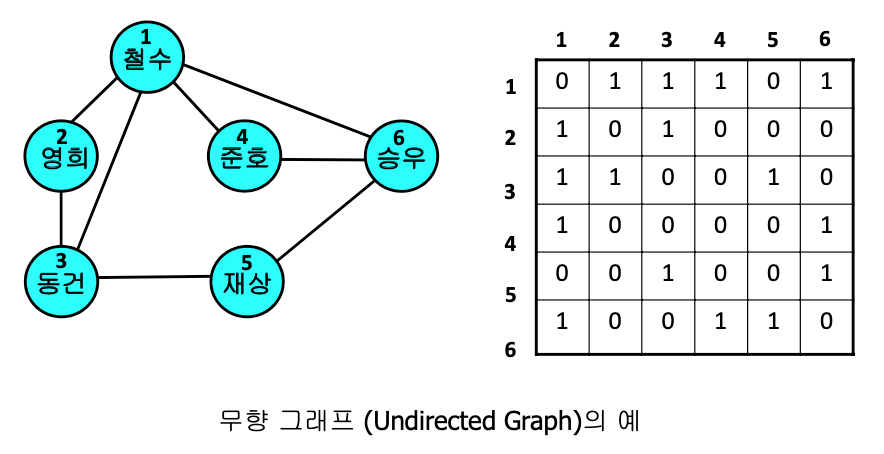
인접행렬

  • N * N 행렬로 표현 (N : 정점의 총 수)
    • 원소 (i, h) = 1 : 정점 i와 정점 j사이에 간선이 있음
    • 원소 (i, j) = 0 : 정점 i와 정점 j사이에 간선이 없음
  • 유향 그래프의 경우
    • 원소 (i, j)는 정점 i로부터 정점 j로 연결되는 간선이 있는지를 나타냄
  • 가중치 있는 그래프의 경우
    • 원소 (i, j)는 1 대신에 가중치를 가짐

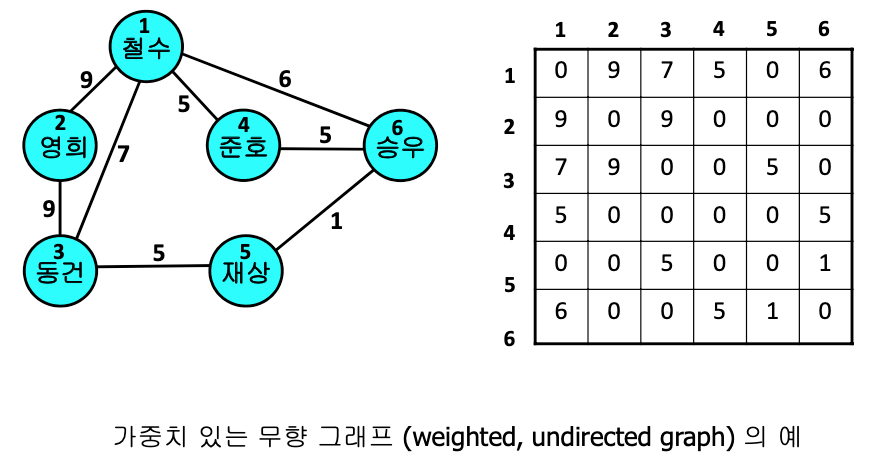
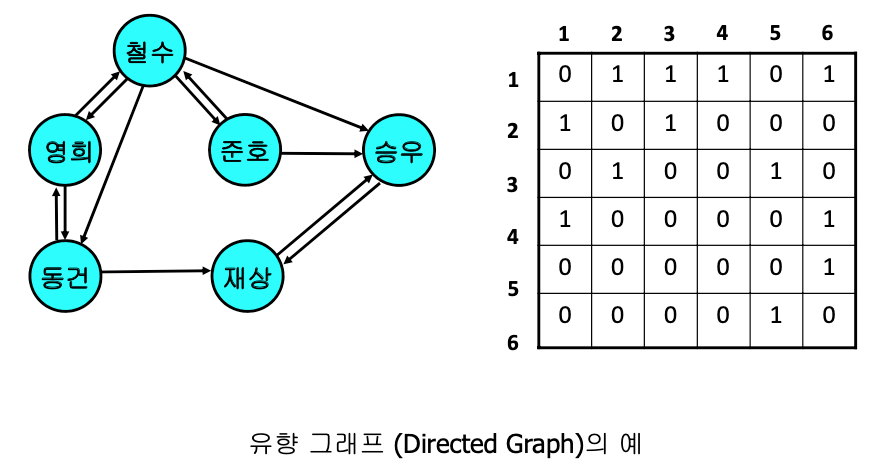
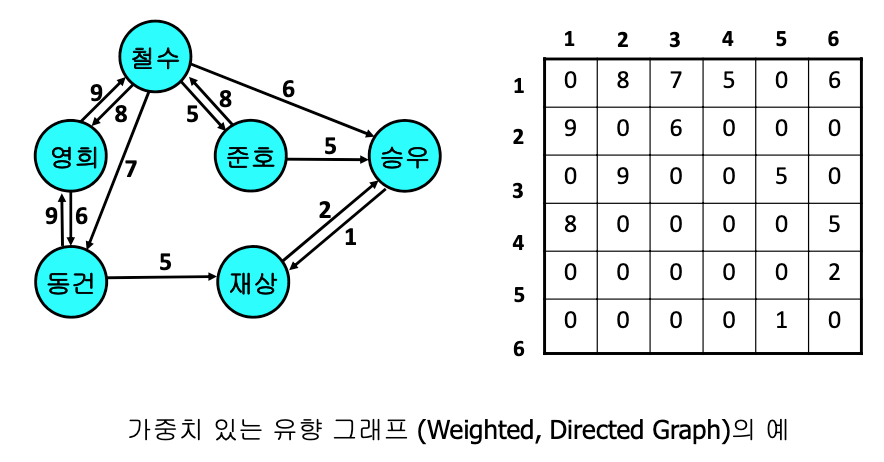
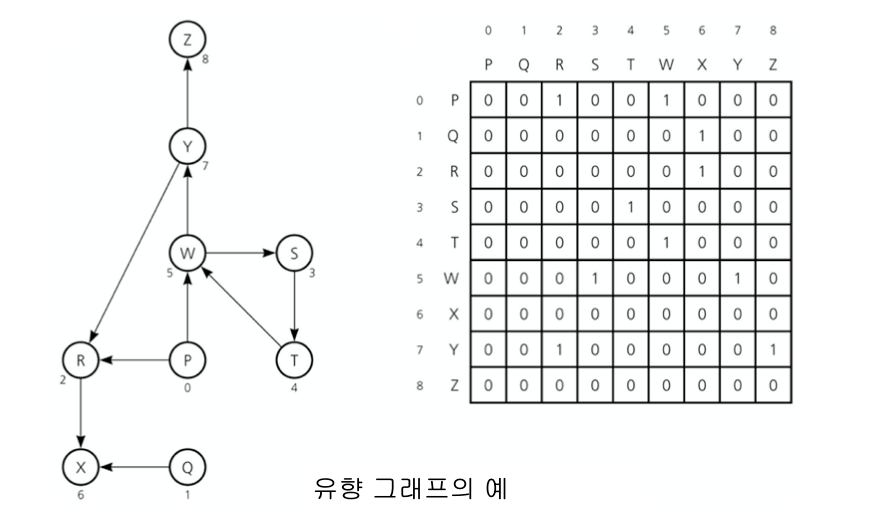
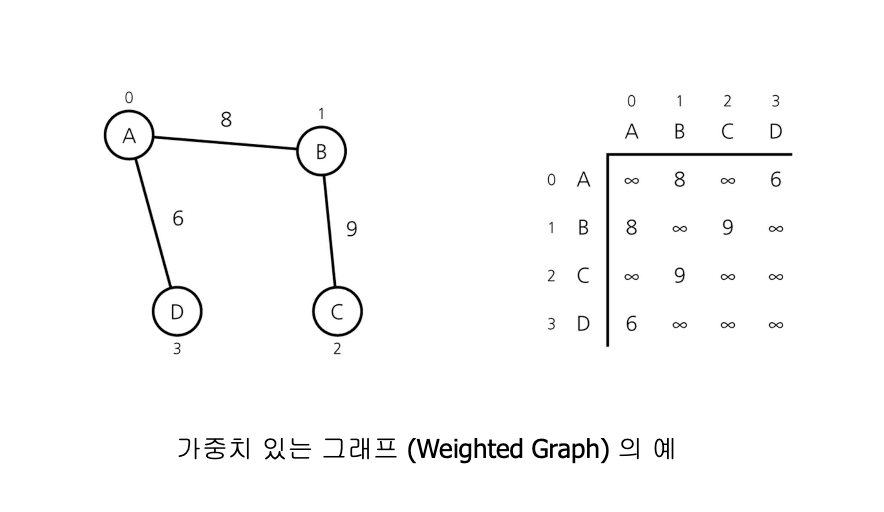
장점 : 인접행렬은 간선간의 밀도가 높은 경우에 유용하고, n^2 이상의 시간이 걸리는 알고리즘에서 적합하다.
단점 :반대의 경우 시간과 공간의 낭비가 발생한다.

인접리스트

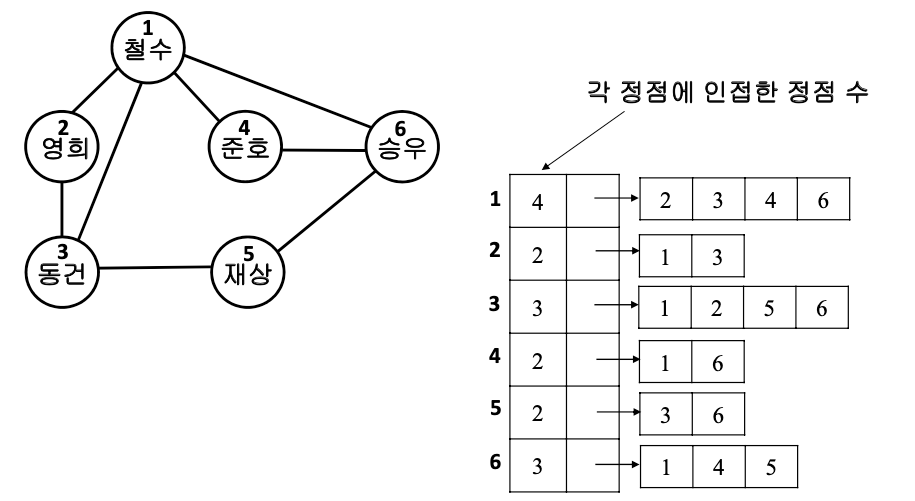
  • N개의 연결 리스트로 표현
  • i번째 리스트는 정점 i에 인접한 정점들을 리스트로 연결해 놓음
  • 가중치 있는 그래프의 경우
    • 리스트에 가중치도 보관한다.

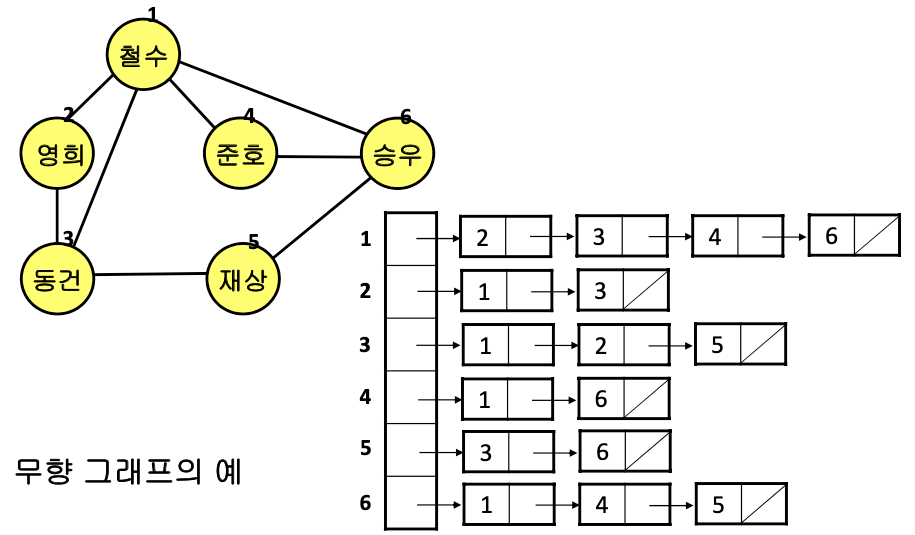
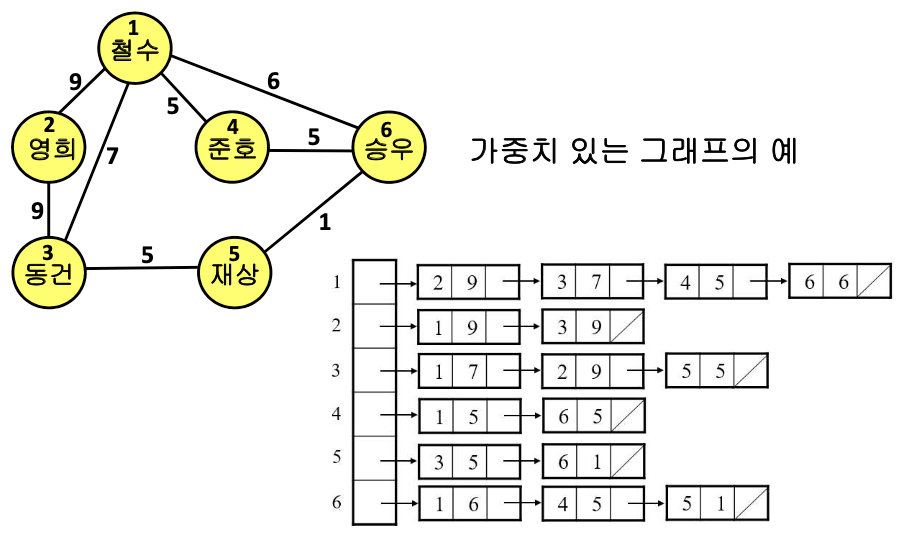
장점 : 행렬 표현에 비해 공간의 낭비가 없다. 모든 가능한 정점 쌍에 비해 간선의 수가 적을 때 유용하다.
단점 : 간선의 밀도가 높은 경우 리스트를 만드는 오버헤드가 커지고, 리스트에 탐색 시간도 존재한다.

인접 배열

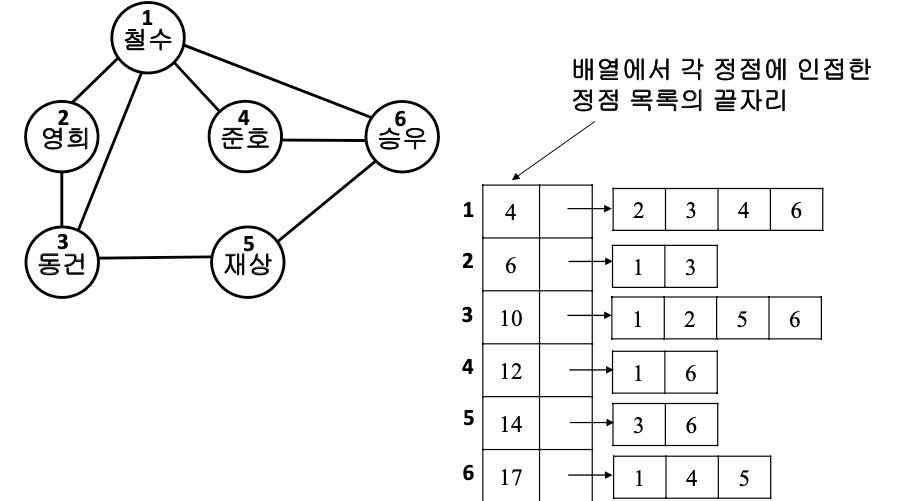
  • N개의 연결 배열로 표현
  • i번째 배열은 정점 i에 인접한 정점들의 집합
  • 가중치 있는 그래프의 경우
    • 리스트에 가중치도 보관한다.

그래프에서 모든 정점 방문하기

  • 대표적 두가지 방법
    • 깊이우선탐색 DFS (Depth-First Search)
    • 너비우선탐색 BFS (Breadth-First Search)

✨✨✨✨✨ 그래프 알고리즘의 기본 ✨✨✨✨✨

동일한 트리를 각각 DFS/BFS로 방문하기

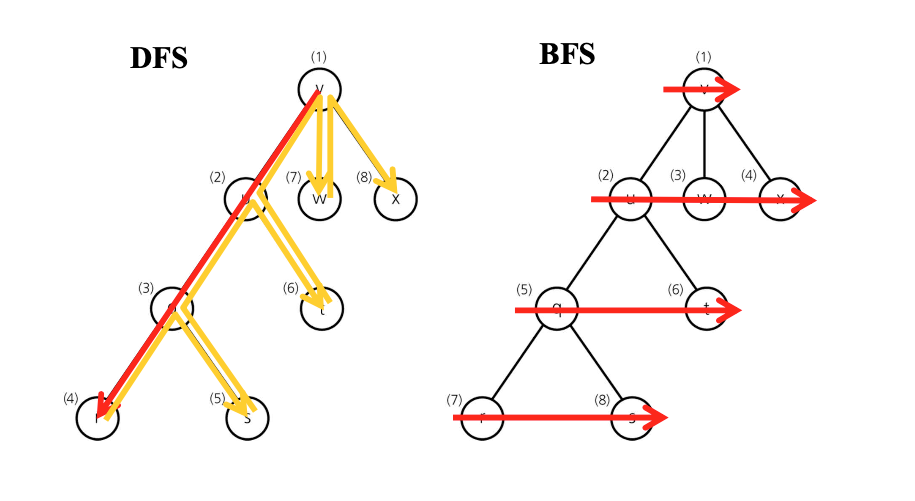
BFS 너비우선탐색

BFS(G, v) {
	for each v ∈ V - {s}
    	visited[v] <- NO;
        
    visited[s] <- YES;				// s : 시작 정점
    	enqueue(Q, s);				// Q : 큐
        while (Q != ∅) {
        	u <- dequeue(Q);
            for each v ∈ L(u)		// L(u): 정점 u의 인접 리스트
            	if (visited[v] = NO) then {
                	visited[u] <- YES;
                    enqueue(Q, V);
                 }
             }
         }
     }
 }
  • Queue를 이용하여 구현
  • 방문여부를 알려주는 visit 배열을 초기화
  • 시작 정점에 방문 기록, 큐에 삽입
  • 반복문 시작
    • 큐에서 반출
    • 반출한 정점에 인접한 정점을 탐색
      • 방문하지 않았던 정점이라면 방문 기록, 큐에 삽입

✔️ 수행시간 : ⊝(|V|+|E|)

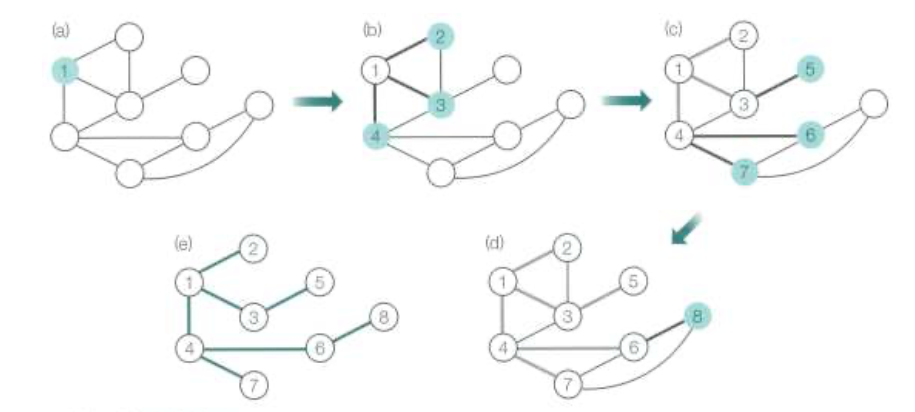
DFS 깊이우선탐색

DFS (v) {
	visited[v] <- YES;
    for each x ∈ L(v)		// L(v) : 정점 v의 인접리스트
   		if (visited[x] = NO) then DFS(x);
  • 재귀함수를 통해 구현

✔️ 수행시간 : ⊝(|V|+|E|)

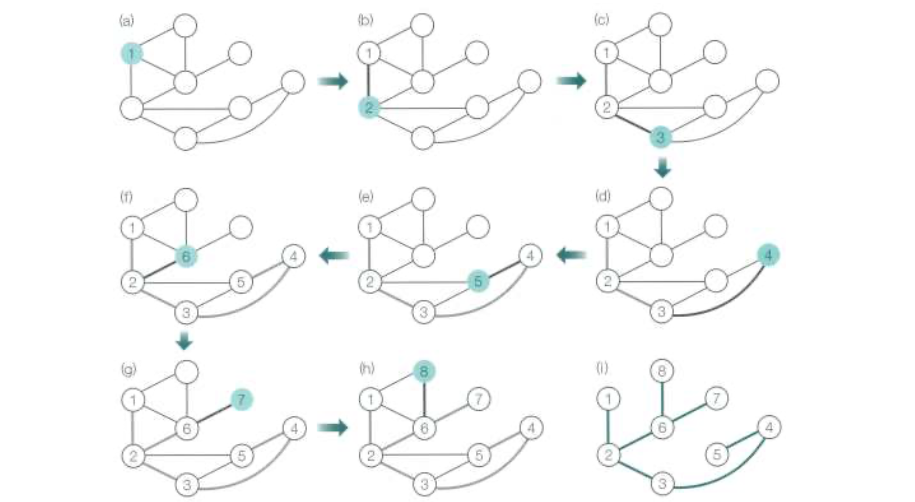
최단경로

  • 조건
    • 간선 가중치가 있는 유향 그래프
    • 무향 그래프는 각 간선에 대해 양쪽으로 유향 간선이 있는 유향 그래프로 생각할 수 있다.
      • 즉, 무향 간선 (u,v)는 유향 간선 (u,v)와 (v,u)를 의미한다고 가정하면 된다.
  • 두 정점 사이의 최단경로
    • 두 정점 사이의 경로들 중 간선의 가중치 합이 최소인 경로
    • 간선 가중치의 합이 음인 싸이클이 있으면 문제가 정의되지 않는다.
  • 단일 시작점 최단경로
    • 단일 시작점으로부터 각 정점에 이르는 최단경로를 구한다.
    • 다익스트라 알고리즘
      • 음의 가중치를 허용하지 않는 최단경로
      • 그리디 알고리즘
    • 벨만-포드 알고리즘
      • 음의 가중치를 허용하는 최단경로
  • 모든 쌍 최단경로
    • 모든 정점 쌍 사이의 최단경로를 모두 구한다.
      -> 플로이드-워샬 알고리즘 (Floyd's 알고리즘)

모든 쌍 최단경로

  • 모든 정점들간의 상호 최단거리 구하기
    • 구해야 할 최단 경로가 모두 n2n^2개
      (자신에게서 자신으로 경로를 포함)
  • 응용 예
    • 도로 지도
    • 네비게이션 시스템
    • 네트워크 커뮤니케이션

1. 동적프로그래밍을 이용

  • 사용하는 간선의 수와 관계되어 변수를 정의
  • dijmd_{ij}^m : 최대 m개의 간선을 사용해서 정점 i에서 정점 j에 이르는 최단 거리

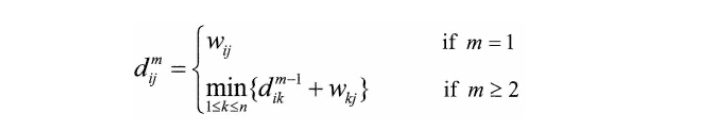
  • 최대 m개의 간선을 사용해서 정점 i에서 정점 j에 이르는 최단 거리 dijmd_{ij}^m 구하기
    --> 모든 정점 k에 대해 최대 m-1개의 간선을 사용해서 정점 k에 이르는 최단거리 dijm−1d_{ij}^{m-1} 에 wkjw_{kj}를 더한 값을 구한 다음 가장 짧은 것을 선택

  • 위 알고리즘은 계산과 구현이 쉬우나 시간이 오래 걸린다.
  • 아래의 알고리즘은 사용하면 변수를 덜 사용하여 구현이 가능하다.
  • dijkd_{ij}^k : 정점 집합 {1,2,3,...,k}에 속하는 정점들만 중간 정점으로 거쳐서 i에서 j에 이르는 최단 거리

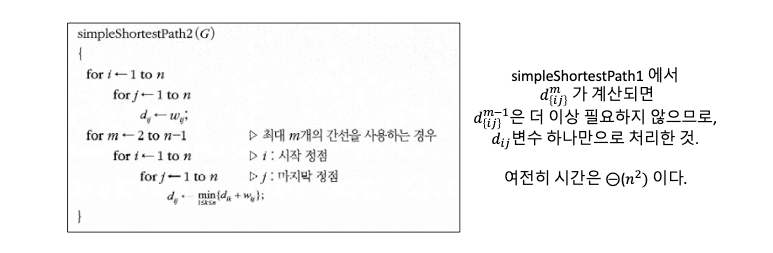
  • 위 알고리즘에서는 간선의 수와 관계지어 변수를 정의하였으나 여기서는 사용한 정점의 집합과 관계를 지었다. 관계식은 다음과 같다.

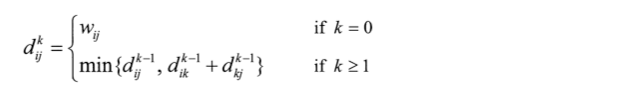
2. 플로이드 알고리즘

  • 그래프에서 최단경로의 길이의 표현 : 0<=k<=n인, dkd^k
    dijmd_{ij}^m = {v1,v2,...,vk}의 정점들 만을 통해서
    vi에서 vj로 가는 최단경로의 길이

  • 사용한 접점의 집합과 관계를 설정

  • 동적계획식 설계전략 - 자료구조

    • 그래프의 인접행렬식 표현 : W

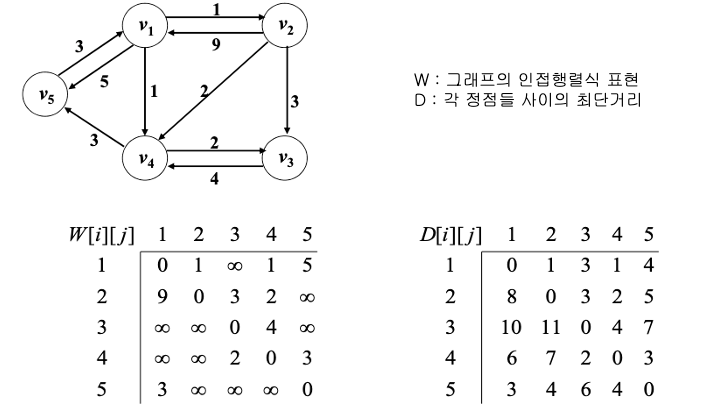
여기서, 0<=k<=5 일때, Dk[2][5]D^k[2][5]를 구해보자.

  • D0D^0 = W이고, Dn=DD^n=D 임은 분명하다. 따라서 D를 구하기 위해서는
    D0D^0을 가지고 DnD^n을 구할 수 있는 방법을 고안해야 한다.

DnD^n: n개의 정점들 사이에서의 최단 거리

  • 재귀관계식 구하기
    • Dk−1D^{k-1}을 가지고 DkD^k 를 계산할수 있는 재귀 관계식을 정립

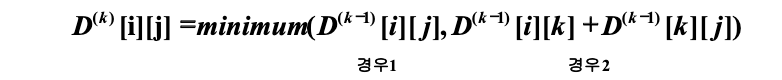
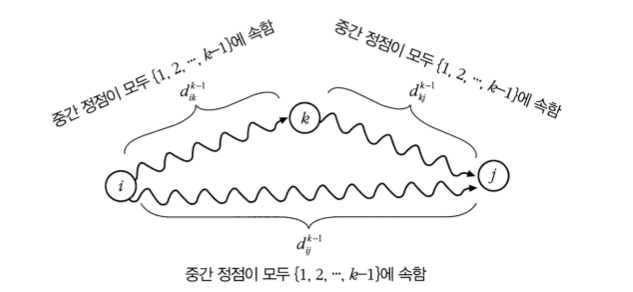
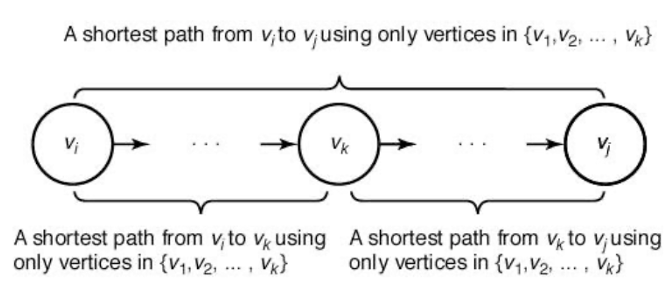
경우 1:{v1,v2,...,vk}의 정점들 만을 통해서 vi에서 vj로 가는 최단경로가 vk를 거치지 않는 경우.
보기 : D5[1][3]=D4[1][3]=3D^{5}[1][3] = D^{4}[1][3]=3

경우 2:{v1,v2,...,vk}의 점점들 만을 통해서 vi에서 vj로 가는 최단경로가 vk를 거치는 경우
보기 : D5[5][3]=D1[5][2]+D1[2][3]=4+3=7D^{5}[5][3] = D^{1}[5][2] + D^{1}[2][3] = 4 + 3 = 7
보기 : D2[5][4]D^{2}[5][4]

  • 상향식으로 k=1부터 n까지 다음과 같이 이 과정을 반복하여 해를 구한다.
    D0,D1,D2,...,DnD^{0},D^{1},D^{2},...,D^{n}

플로이드 알고리즘 1

  • 문제
    • 가중치 포함 그래프의 각 정점에서 다른 모든 정점까지의 최단거리를 계산하라
    • 입력
      • 가중치 포함, 방향성 그래프 W와 그 그래프에서의 정점의 수 n
    • 출력
      • 최단거리의 길이가 포함된 배열 D
  • 알고리즘
  void floyd ( int n, const number W[][], number D[][]) {
  	int i, j, k;
    D = W;
    for (k=1; k<=n; k++)
    	for (i=1; i<=n; i++)
        	for (j=1; j<=n; j++)
            	D[i][j] = minimum(D[i][j], D[i][k]+D[k][j]); // k루프
  }
  • 모든 경우를 고려한 분석
    • 단위연산 : for-j 루프안의 지정문
    • 입력크기 : 그래프에서의 정점의 수 n
      T(n)= n x n x n = n3n^3 ∈ ⊝(n3n^3)

플로이드 알고리즘 2

  • 문제

    • 가중치 포함 그래프의 각 정점에서 다른 모든 정점까지의 최단거리를 계산하고, 각각의 최단경로를 구하라.

    • 입력

      • 가중치 포함 방향성 그래프 W와 그 그래프에서의 정점의 수 n

    • 출력

      • 최단경로의 길이가 포함된 배열 D, 그리고 다음을 만족하는 배열 P

  • 알고리즘
void floyd2(int n, const number W[][], number D[][], index P[][]) {
	index i, j, k;
    
    for(i=1; i<=n; i++)
    	for(j=1; j<=n; j++)
        	P[i][j] = 0;
    D = W;
    for (k=1; k<=n; k++)
    	for(i=1; i<=n; i++)
        	for(j=1; j<=n; j++)
            	if ( D[i][k] + D[k][j] < D[i][j] ) {
		    P[i][j] = k;
                    D[i][j] = D[i][k] + D[k][j];
                }     
 }

profile
이상현
'당신을 한 줄로 소개해보세요'를 이 블로그로 대신 해볼까합니다.
이전 포스트

[알고리즘] 그리디 알고리즘

0개의 댓글