[알고리즘] 그리디 알고리즘

이상현·2020년 11월 7일
0

알고리즘_강의노트

목록 보기
7/8
post-thumbnail

그리디 알고리즘

개요

  • 눈앞의 이익만 취하고 보는 알고리즘
  • 현재 시점에 가장 이득이 되어 보이는 해를 선택하는 행위를 반복
  • 대부분 최적해와의 거리가 멀다
  • 드물게 최적해가 보장되는 경우가 있다.
do {
	우선 가장 좋아보이는 선택을 한다.
} until 문제의 끝까지
  • optimization 문제를 해결할 때 이용
    : DP 또는 Greedy를 사용해서 문제를 해결
    • DP : 재귀방정식을 사용해서 작은 문제로 쪼개어 해결
    • Greedy : 그 순간 가장 좋아보이는 선택을 한다. (Locally optimal)

그리디 알고리즘은 결정을 해야 할 때마다 그 순간에 가장 좋다고 생각되는 것을 해답으로 선택함으로써 최종적인 해답에 도달한다.

그 순간의 선택은 그 당시(local)에는 최적이다. 그러나 최적이라고 생각했던 해답들을 모아서 최종적인(global) 해답을 만들었다고 해서, 그 해답이 궁극적으로 최적이라는 보장이 없다.

따라서 그리디 알고리즘은 항상 최적의 해답을 주는지를 반드시 검증해야 한다.

설계 절차

1. Selection procedure (선정과정)

: 현재 상태에서 가장 좋으리라고 생각되는 (greedy criterion) 해답을 찾아서 해답 모음 (solution set)에 포함시킨다.

2. Feasibility check (적정성 점검)

: 새로 얻은 해답 모음이 적절한지를 결정한다.

3. Solution check (해답 점검)

: 새로 얻은 해답모음이 최적의 해인지를 결정한다.

Example

거스름돈 문제

  • problem : 동전의 개수가 가장 최소가 되도록 거스름 돈을 주는 문제
  • Greedy Algorithm
while (there are more coins and the instance is not solved) {
	Grab the largest remaining coin;	// 선정과정
    
    if ( adding the coin makes the change exceed the amount owed){
    	reject the coin;			// 적정성 점검
    }
    else
    	add the coin to the change;
    
    if ( the total value of the change equals the amount owed )
    	the instance is solved;			// 해답 점검
 }

그리디 알고리즘으로 최적해가 보장되지 않는 예

  1. 이진 트리의 최적합 경로 찾기

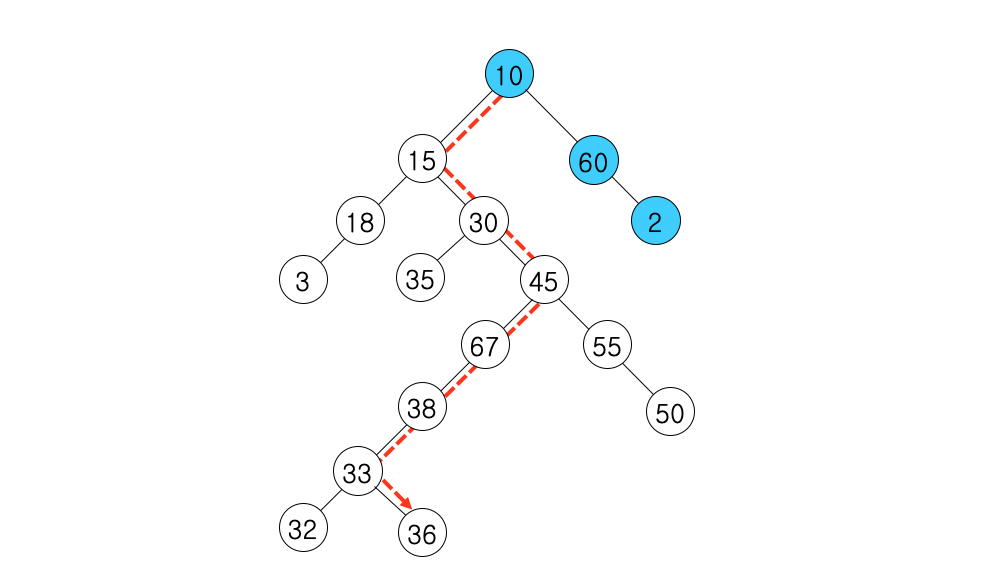
: 현재 상태에서의 최적만을 찾기 때문에, 비교하는 현재 노드의 자식노드를 고려하지 못함. 따라서 최종적으로 최적해가 아닐 가능성이 있다.

  1. 액면이 바로 아래 액면의 배수가 되지 않을 때의 거스름돈 문제

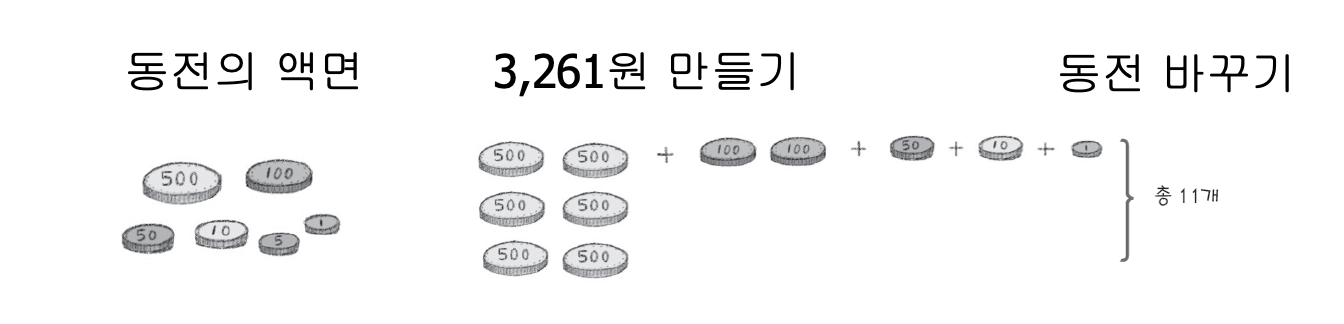
: 동전의 액면이
500원, 100원, 50원, 10원, 5원, 1원 으로 구성되어 있다.

  • 500원 = 100원 * 5
  • 100원 = 50원 * 2
  • 50원 = 10원 * 5
  • 10원 = 5원 * 2
  • 5원 = 1원 * 5
    와 같이 모든 액면이 바로 아래 액면의 배수가 된다면, 그리디 알고리즘으로 최적해가 보장된다.

하지만, 액면이 바로 아래 액면의 배수가 되지 않으면, 그리디 알고리즘으로 최적해가 보장되지 않게 된다.

: 동전의 액면이
500원, 400원, 100원, 75원, 50원 으로 구성되어 있다.

  • 500원 = 400원 * 1.xxx
  • 100원 = 75원 * 1.xxx
    으로 액면이 바로 아래 액면의 배수가 되지 않으면, 그리디 알고리즘으로 최적해가 보장되지 않는다.

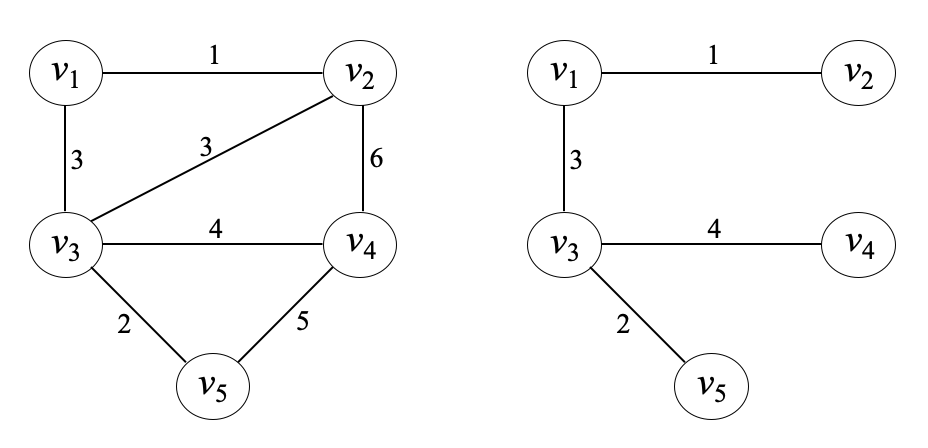
Spanning Tree

  • 연결된, 비방향성 그래프에서 G에서 순환경로를 제거하면서 연결된 부분그래프가 되도록 이음선을 제거
  • 따라서 신장트리는 G안에 있는 모든 정점을 다 포함하면서 트리가 되는 연결된 부분그래프

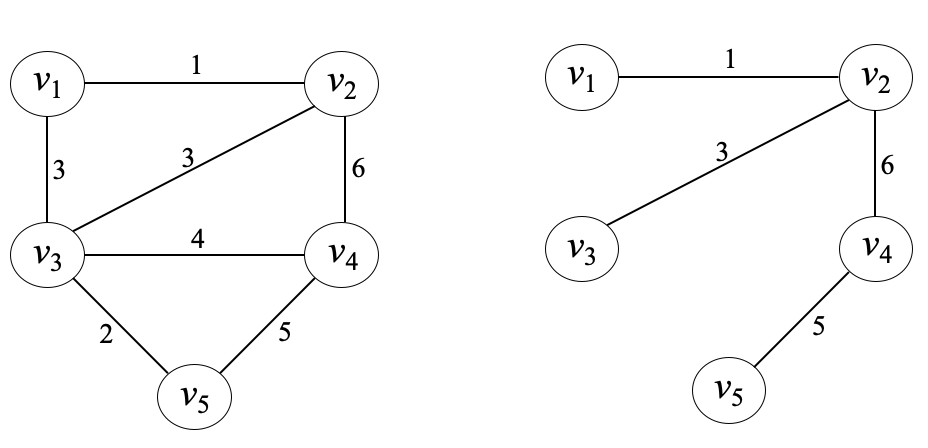
: 좌측은 연결된 가중치 비방향 그래프, 우측은 Spanning Tree의 예

Minimum Spanning Tree

  • 최소의 가중치를 가진 부분그래프는 반드시 트리가 되어야 한다. 왜냐하면, 트리가 아니라면, 분명히 순환경로(Cycle)가 있을 것이고, 그렇게 되면 순환경로 상의 한 이음선을 제거하면 더 작은 비용의 신장트리가 되기 때문이다.

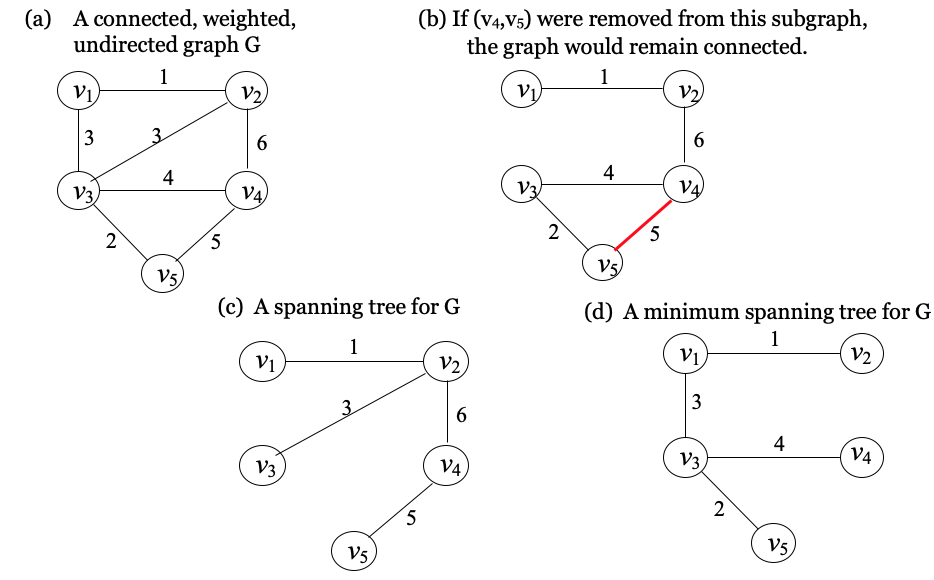
  • 관찰 : 모든 신장트리가 최소비용 신장트리는 아니다.

: 좌측은 연결되 가중치 비방향 그래프, 우측은 Minimum Spanning Tree의 예

과정

적용 예

  • 도로 건설 : 도시들을 모드 연결하면서 도로의 길이가 최소가 되도록 하는 문제
  • 통신 : 전화선의 길이가 최소가 되도록 전화 케이블 망을 구성하는 문제
  • 배관 : 파이프의 총 길이가 최소가 되도록 연결하는 문제

그리디 접근법을 사용한 MST 구하기

  • problem : 비방향성 그래프 G=(V,E)가 주어졌을 때, F⊆E를 만족하면서, (V,F)가 G의 최소비용신장트리(MST)가 되는 F를 찾는 문제.

  • Algorithm

F = ∅
while (the instance is not solved) {
	select an edge according to some locally	# selection procedure
    	optimal consideration;
       
    if (adding the edge to F dose not create a cycle)
    	add it;						# feasibility procedure
    if ( T = (V,F) is a spanning tree)			# solution check
    	the instance is solved;
}

Prim's Algorithm

  • Algorithm
F = ∅;			# initialize set of edges to empty
Y = {v1};		# initialize set of vertices to
				# contain only the first one

while ( the instance is not solved ) {
	select a vertex in V-Y that is nearest to Y;
    				# selection procedure and
				# feasibility check
    add the vertex to Y;
    add the edge to F;

	if ( Y==V )		# solution check
    	the istance is solved;
}

과정

예 1)

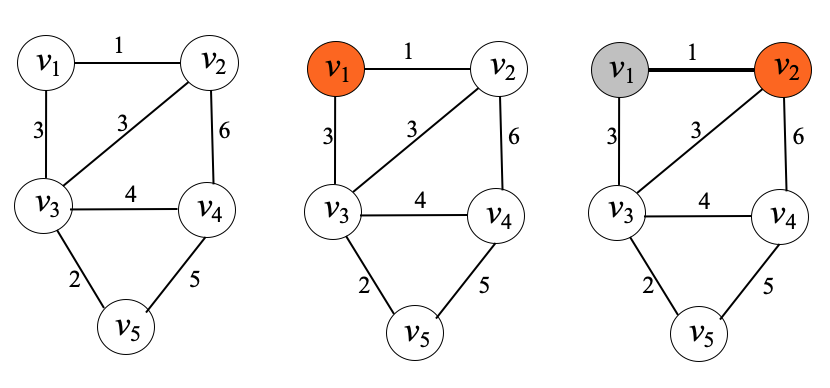
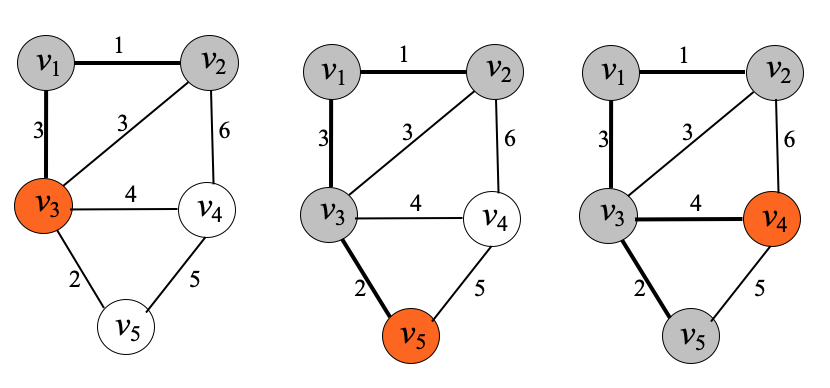
예 2)

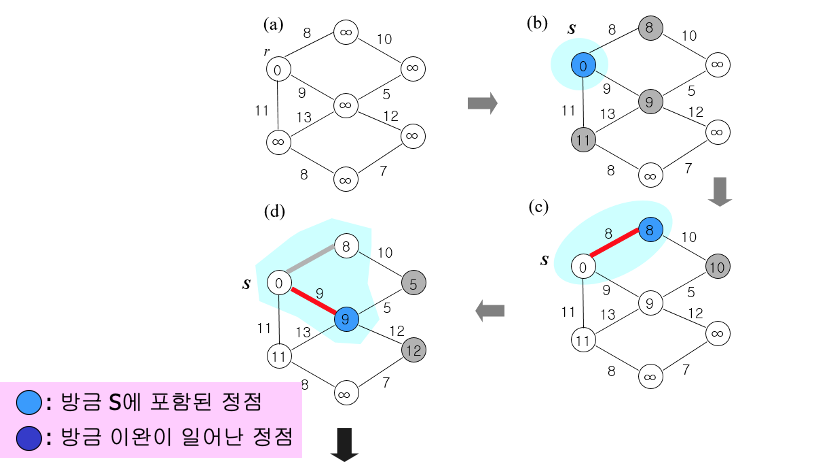
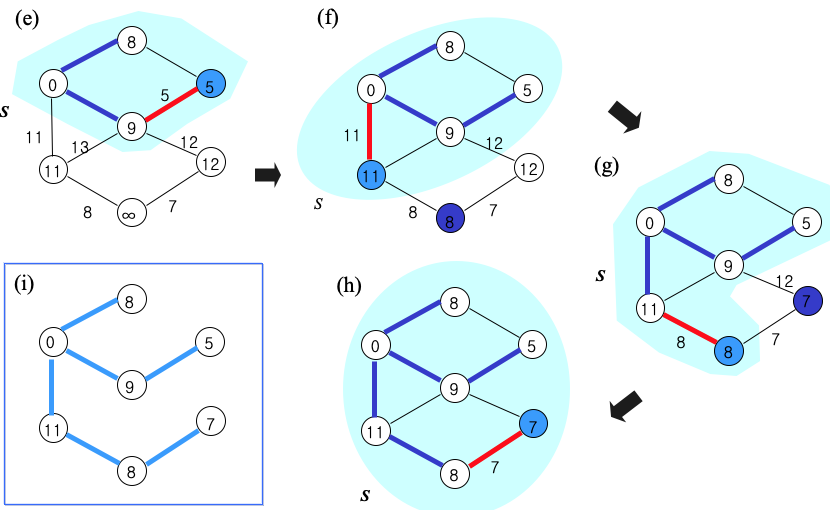
Code

void prim ( int n, const number W[][], set_of_edges& F){
	index i, vnear; number min; edge e;
    index nearest[2..n]; number distance[2..n]
    
    F=∅;
    for ( i=2; i<=n; i++ ){		# 초기화
    	nearest[i] = 1;			# vi에서 가장 가까운 정점을 v1으로 초기화
        distance[i] = W[1][i];
    }
    repeat(n-1 times) {			# n-1 개의 정점을 Y에 추가한다
    	min = "infinite";
        for (i=2; i<=n; i++)		# 각 정점에 대해서
        	if ( 0<=distance[i]<=min){ # distance[i]를 검사하여
            	min = distance[i];	# 가장 가까이 있는 vnear을
                vnear = i;		# 찾는다.
            }
        e = edge connecting vertices indexed by vnear and nearest[vnear];
        add e to F;
        distance[vnear] = -1;		# 찾은 노드를 Y에 추가한다.
        for ( i=2; i<=n; i++ )
        	if (W[i][vnear] < distance[i]){
            	distance[i] = W[i][vnear]; # Y에 없는 각 노드에 대해서
                nearest[i] = vnear; 	   # distance[i]를 갱신한다.
            }
    }
}

Every-case Time Complexity Analysis

  • 단위연산 : repeat-루프 안에 있는 두 개의 for-루프 내부에 있는 명령문
  • 입력크기 : 마디의 개수, n
  • 분석 : repeat-루프가 n-1번 반복되므로
    T(n) = 2(n-1)(n-1) ∈ ⊝(n2)(n^2)

최적여부의 검증 (Optimality Proof)

  • Prim의 알고리즘이 찾아낸 신장트리가 최소비용(minimal)인지를 검증
  • Definition : 비방향성 그래프 G=(V,E)가 주어지고, 만약 E의 부분집합 F에 MST가 되도록 이음선을 추가할 수 있으면, F는 유망하다(promising)라고 한다.
  • Lemma : G=(V,E)는 연결되고, 가중치 포함 비방향성 그래프라고 하고, F는 E의 유망한 부분집합이라고 하고, Y는 F안에 있는 이음선 들에 의해서 연결이 되어 있는 정점의 집합이라고 하자.
    이떄, Y에 있는 어떤 정점과 V-Y에 있는 어떤 정점을 잇는 이음선 중에서 가중치가 가장 작은 이음선을 e라고 하면, F∪{e}는 유망하다.
  • F가 유망하기 때문에 F⊆F'이면서 (V,F')가 최소비용신장트리가 되는 이음선의 집합 F'가 반드시 존재한다.
  • 경우 1 : 만일 e∈F'라면, F∪{e}⊆F'가 되고, 따라서 F∪{e}도 유망하다.
  • 경우 2 : 만일 e∉F'라면, (V,F')는 신장트리이기 때문에, F'∪{e}는 반드시 순환경로를 하나 포함하게 되고, e는 반드시 그 순환경로 가운데 한 이음선이 된다.
    • 그러면 Y에 있는 한 정점에서 V-Y에 있는 한 정점을 연결하는 어떤 다른 이음선 e'∈F'가 그 순환경로 안에 반드시 존재하게 된다.
    • 여기서 만약 F'∪{e}에서 e'를 제거하면, 그 순환경로는 없어지게 되며, 다시 신장트리가 된다. 그런데 e는 Y에 있는 한 정점에서 V-Y에 있는 한 정점을 연결하는 최소의 가중치(weight)를 가진 이음선이기 때문에, e의 가중치는 반드시 e'의 가중치보다 작거나 같아야 한다.(실제로 반드시 같게 된다.)
    • 그러면 F'∪{e}-{e'}는 최소비용신장트리(MST)이다.
    • 결론적으로 e'는 F안에 절대로 속할 수 없으므로 (F안에 있는 이음선들은 Y안에 있는 정점들 만을 연결함을 기억하라),
      F∪{e}⊆F'∪{e}-{e'}가 되고, 따라서 F∪{e} 유망하다.

증명

  • 정리 : Prim의 알고리즘은 항상 최소비용신장트리를 만들어 낸다.
  • 증명 (수학적귀납법)
    : 매번 반복이 수행된 후에 집합 F가 유망하다는 것을 보이면 된다.
    • 출발점 : 공집합은 당연히 유망하다.
    • 귀납가정 : 어떤 주어진 반복이 이루어진 후, 그때까지 선정하였던 이음선의 집합인 F가 유망하다고 가정한다.
    • 귀납절차 : 집합F∪{e}가 유망하다는 것을 보이면 된다. 여기서 e는 다음 단계의 반복 수행 시 전정된 이음선 이다.
      그런데, 위의 보조정리 1에 의하여 F∪{e}은 유망하다고 할 수 있다. 왜냐하면 이음선 e는 Y에 있는 어떤 정점을 V-Y에 있는 어떤 정점으로 잇는 이음선 중에서 최소의 가중치를 가지고 있기 때문이다.

Kruskal's Algorithm

  • Algorithm
F = ∅			# initialize set of edges
			# to empty
create disjoint subsets of V, one for each
vertex and comtaining only that vertex;

sort the edges in E in nondecreasing order;

While ( the instance is not solved ) {
	select next edge;	# selection procedure
    if ( the edge connects 2 vertices in disjoint subsets ) {
	    			# feasibility check
    	merge the subsets;
        add the edge to F;
    }
    if ( all the subsets are merged ) # solution check
    	the instnace is solved;
}

과정

예 1)

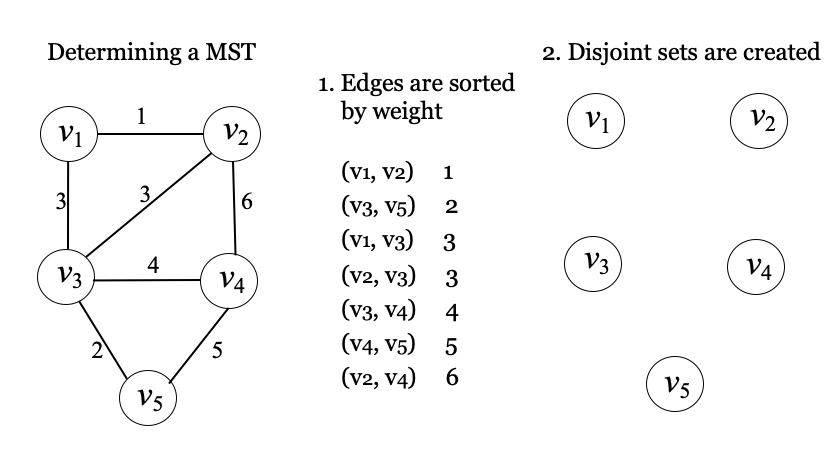
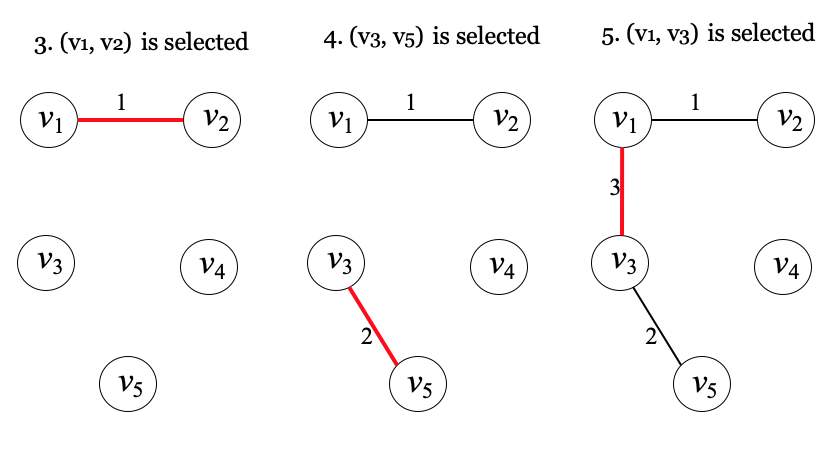
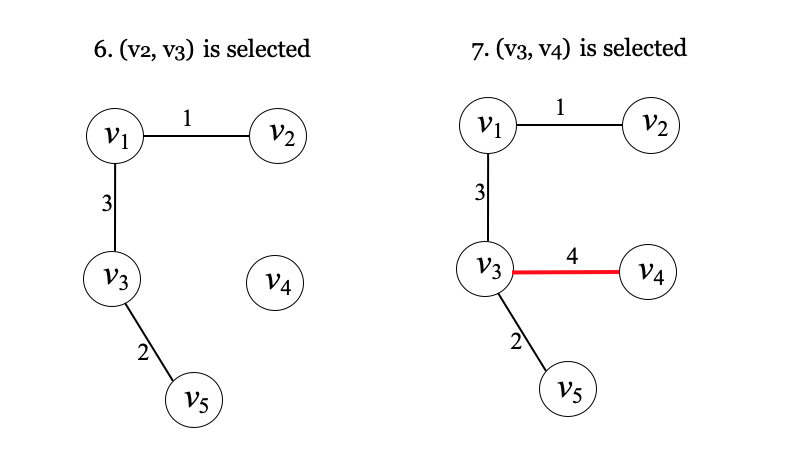
예 2)

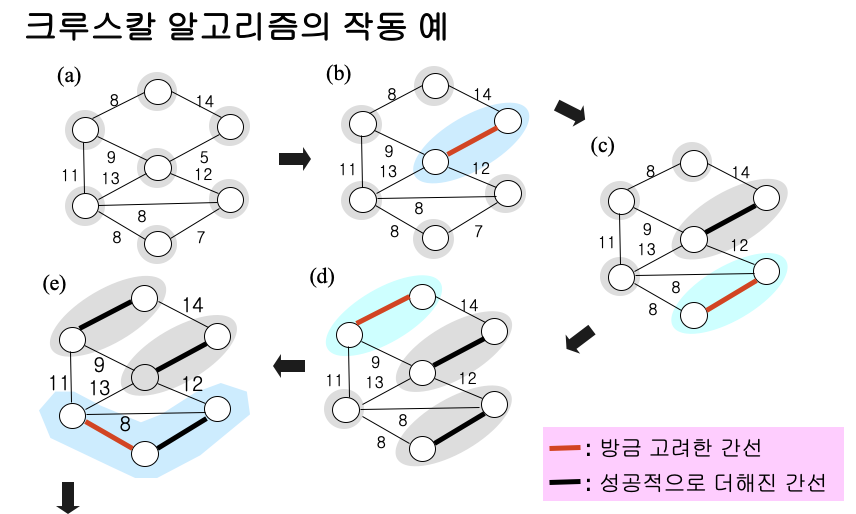
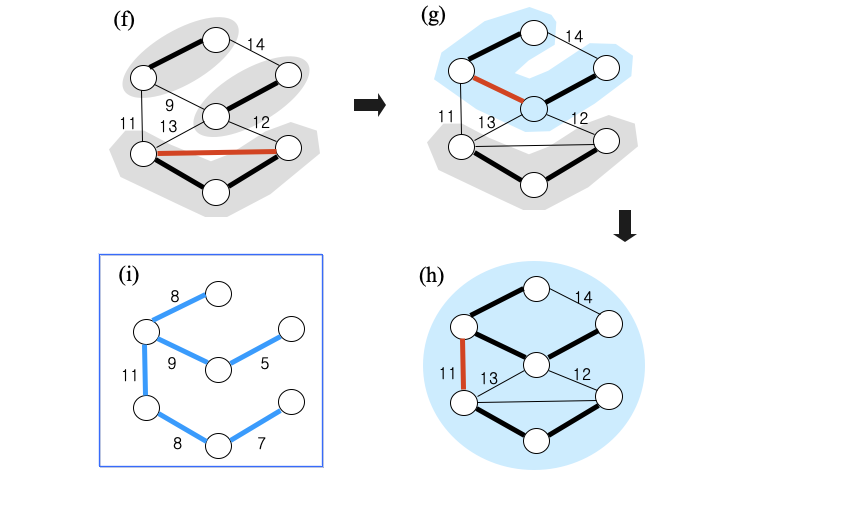
Code

void kruskal (int n, int m. set_of_edges E, set_of_edges& F) {
	index i,j;
    set_pointer p, q;
    edge e;
    
    Sort the m edges in E by weight in nondecreasing order;
    F = ∅;
    initial(n);		# n개의 서로소 부분집합을 초기화
    			# (하나의 부분집합에 1에서 n사이의 인덱스가 정확히 하나 포함됨)
    
    While (number of edges in F is less than n-1) {
    	e = edges with least weight not yet considered;
        i,j = indices of vertices connected by e;
        p = find(i);    # 인덱스 i가 포함된 집합의 포인터 p를 넘겨줌
        q = find(j);
        if ( !equal (p,q) {     # p와 q가 같은 집합을 가리키면 true를 넘겨줌 
        	merge(p,q);	# 두 개의 집합을 가리키는 p와 q를 합병
            add e to F;	
        }
    }
}

Worst-Case Time-Complexity Analysis

  • 단위연산 : 비교문
  • 입력크기 : 정점의 수 n과 이음선의 수 m
    1. 이음선들을 정렬하는데 걸리는 시간 : ⊝(m lg m)
    1. 반복문 안에서 걸리는 시간 : 루프를 m번 수행한다. 서로소인 집합 자료구조 (disjoint set data structure)를 사용하여 구현하고, find, equal, merge 같은 동작을 호출하는 횟수가 상수이면, m개의 이음선 반복에 대한 시간복잡도는 ⊝(m lg m)이다.
    2. n개의 서로소인 집합(disjoint set)을 초기화하는데 걸리는 시간 : ⊝(n)
  • 그런데 여기서 m>=n-1이기 때문에, 위의 1과 2는 3을 지배하게 되므로, W(m,n)=⊝(m lg m)가 된다.
  • 그러나, 최악의 경우에는 모든 정점이 다른 모든 정점과 연결이 될 수 있기 때문에, m=(n(n−1))/2)∈⊝(n2)m=(n(n-1))/2)∈⊝(n^2) 가 된다. 그러므로, 최악의 경우의 시간복잡도는
    W(m,n)∈⊝(n2lgn2)=⊝2n2lgn)=⊝(n2lgn)W(m,n)∈⊝(n^2 lg n^2)=⊝2n^2lgn)=⊝(n^2lgn)
  • 최적여부의 검증 (Optimality Proof)
    • Prim의 알고리즘의 경우와 비슷함.

두 알고리즘의 비교

최단경로 - Dijkstra's Algorithm

  • 가중치가 있는 방향성 그래프에서 한 특정 정점에서 다른 모든 정점으로 가는 최단경로 구하는 문제
  • 시작점 v1
  • 알고리즘
F = 0;
Y = {v1};
While ( the instance is not solved )
 # selection procedure
	select a vertex v from V-Y, that has a shortest path
 # and feasibility check
   	from v1, using only vertices in Y as intermediate;   
    
    add the new vertex v to Y;
    add the edge (on the shortest) that touches v to F;
 # solution check
    if( Y == V ) #
    	the instance is solved;

과정

예 1)

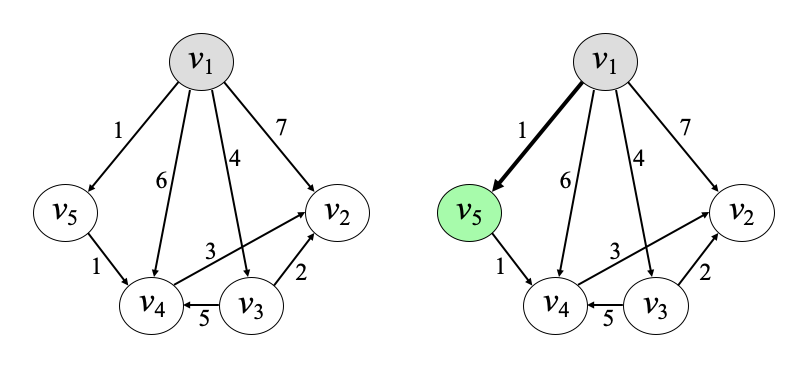
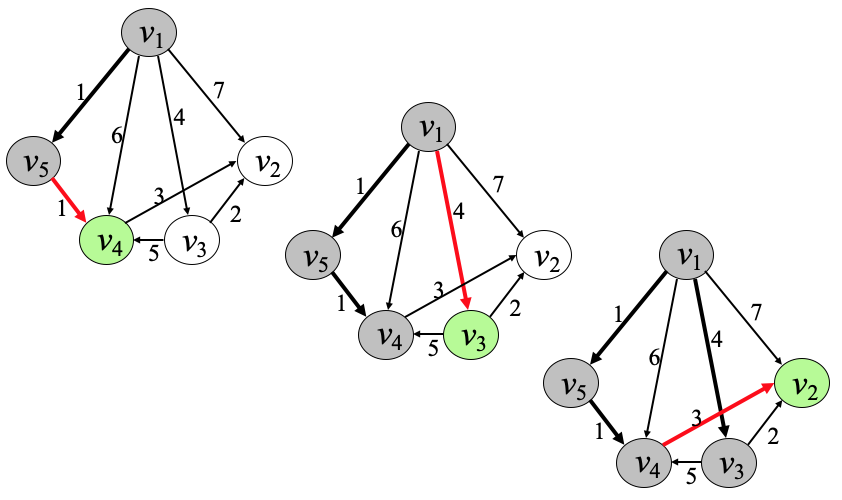
예 2)

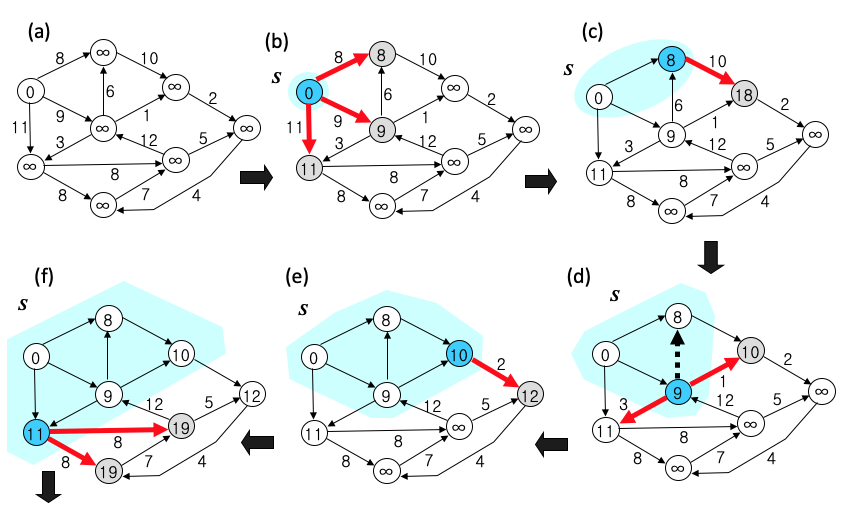
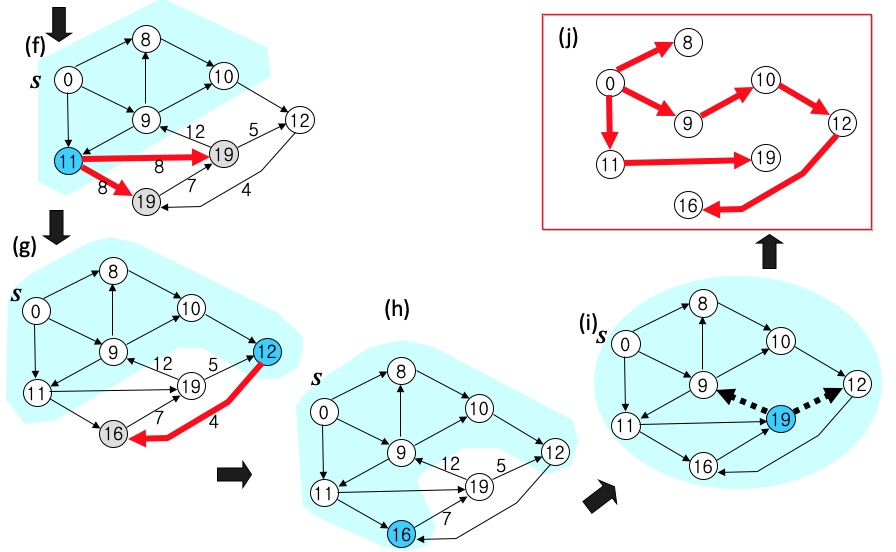
Code

void dijkstra ( int n, const number W[][], set_of_edges& F ) {
	index i, vnear; edge e;
    index touch[2..n]; number length[2..n];
    
    F=∅;
    for (i=2; i<=n; i++) {	# For all vertices, initialize v1 to be the last
    	touch[i] = 1;		# vertex on the current shortest path from v1,
        length[i] = W[1][i];	# and initialize length of that path to be the
    }				# weight on the edge from v1
    repeat(n-1 times) {		# Add all n-1 vertices to Y.
    	min = "infinite";
        for ( i=2; i<=n; i++ )	# Check each vertex for having shortest path.
        	if ( 0 <= length[i] <= min ){
            	min = length[i];
                vnear = i;
            }
        e = edge from vertex indexed by touch[vnear]
           to vertex indexed by vnear;
        add e to F;
        for ( i=2; i<=n; i++ )
            if ( length[vnear] + W[vnear][i] < length[i]) {
            	length[i] = length[vnear] + W[vnear][i];
                touch[i] = vnear; # For each vertex not in Y, update its shortest
            }			  # path. Add vertex indexed by vnear to Y.
        length[vnear] = -1;
    }
}

분석

  • T(n)=2(n−1)2∈⊝(n2)T(n) = 2(n-1)^2 ∈ ⊝(n^2)

최적 여부의 검증 (Optimality Proof)

  • Prim의 알고리즘의 경우와 비슷함.
profile
이상현
'당신을 한 줄로 소개해보세요'를 이 블로그로 대신 해볼까합니다.
이전 포스트

[알고리즘] 정렬

다음 포스트

[알고리즘] 그래프

0개의 댓글