[알고리즘] 점화식과 알고리즘 복잡도 분석

점화식의 이해

점화식 : 어떤 함수를 자신보다 더 작은 변수에 대한 함수와의 관계로 표현한 것

예) 병합 정렬의 수행 시간

mergeSort( A[ ], p, r){
	if (p < r) then {
    	q = floor(p+q)/2);    // p,q의 중간 지점 계산
        mergeSort(A, p, q);   // 전반부 정렬
        mergeSort(A, q+1, r); // 후반부 정렬
        merge(A, p, q, r);	  // 병합
    }
}

merge(A[ ], p, q, r){
	정렬되어 있는 두 배열 A[p ... q]와 A[q+1 ... r]을 합하여
   	정렬된 하나의 배열 A[p ... r]을 만든다.
}
        

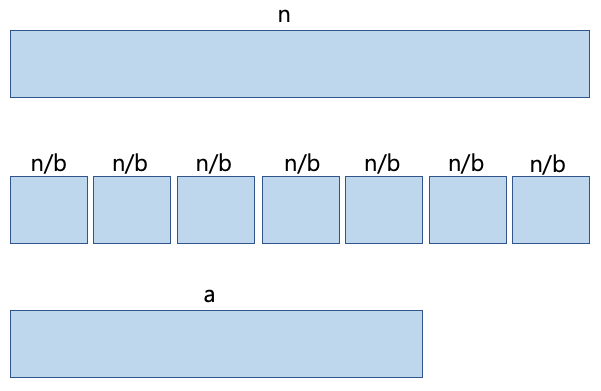
- 수행시간의 점화식 : T(n) = 2*T(n/2) + 오버헤드
✔️ 크기가 n인 병합 정렬 시간은 크기가 n/2인 병합정렬을 두 번하는 시간과 나머지 오버헤드를 더한 시간이다.

점화식 분석 방법

◼︎ 점화식의 점근적 분석 방법
1. 반복 대치
     : 더 작은 문제에 대한 함수로 반복해서 대치해 나가는 해법
2. 추정 후 증명
     : 결론을 추정하고 수학적 귀납법을 이용하여 증명하는 방법
3. 마스터 정리
     : 형식에 맞는 점화식의 복잡도를 바로 알 수 있다.

1. 반복 대치

: 더 작은 문제에 대한 함수로 반복해서 대치해 나가는 해법

(예1)

$T(n) = T(n-1) + c$ 이고,
$T(1)≤c$ 이면

$T(n) = T(n-1) + c$
         $=(T(n-2)+c)+c = T(n-2)+2c$
         $= (T(n-3)+c)+2c = T(n-3)+3c$
         ...
         $=T(1)+(n-1)c$
         $≤c+(n-1)c$
         $=cn$

$T(n)≤cn$ = $O(n)$

(예2)

$T(n) = 2T(n/2) + n$   ($2^k = n$이라고 가정) // $n=2^k=>log_2n = k$로 변환 가능
$T(1)=1$

$T(n) = 2T(n/2) + n$
          $=2(2T(n/2^2)+n/2)+n= 2^2T(n/2^2)+2n$
          $=2^2(2T(n/2^3)+n/2^2)+n= 2^3T(n/2^3)+3n$
          ...
          $=2^kT(n/2^k)+kn$   // 가정에 따라 변환
          $=n + nlogn$
          $=⊝(nlogn)$

2. 추정 후 증명

: 결론을 추정하고 수학적 귀납법을 이용하여 증명하는 방법

(예1)

$T(n) = 2T(n/2)+n$
추정 : $T(n)=O(nlogn), 즉 T(n)≤cnlogn$
증명 :
$T(n) = 2T(n/2) + n$
         $≤2c(n/2)log(n/2)+n$
         $=cnlogn - cnlog2+n$  // $log(n/m) = logn-logm$으로 변경 가능
         $=cnlogn + (-clog2+1)n$
         만약, $c=1/log2$ 라면
          $(1/log2)nlogn ≤ cnlogn$ 이 성립한다.

(예 2-1)

$T(n) = 2T(n/2)+1$
추정 : $T(n)=O(n), 즉 T(n)≤cn$
증명 :
$T(n) = 2T(n/2) + 1$
         $≤2c(n/2)+1$ ← 귀납적 가정 이용
         $=cn+1$
더 이상 진행 불가! ( $T(n)≤cn$ 을 만족하지 않음)

(예 2-2)

앞의 $T(n) = 2T(n/2)+1$
추정 : $T(n)≤cn-2$
증명 :
$T(n) = 2T(n/2) + 1$
         $≤2c(n/2-2)+1$ ← 귀납적 가정 이용
         $=cn-3$
         $≤cn-2$ 이 성립한다.
따라서 $T(n)=O(n)$ 를 만족한다.

3. 마스터정리

: 형식에 맞는 점화식의 복잡도를 바로 알 수 있다.

• $T(n)=aT(n/b)+f(n)$ 와 같은 모양을 가진 점화식은 마스터 정리에 의해 바로 결과를 알 수 있다.

• $n^{log_ba}=h(n)$ 이라 하자

  마스터정리는 일종의 devide and conquer. 기존의 n을 b개로 나누어 처리 후, a개를 합치는 방식.
  

  a: 합치는 개수, b: 나누는 개수, f(n): 병합시 소요되는 오버헤드 를 표현

◼︎ 근사버전
1. $lim_{n→∞}f(n)/h(n) = 0$ 이면 (h(n)이 크다면), $T(n) = ⊝(h(n))$ 이다.
2. $lim_{n→∞}f(n)/h(n) = ∞$ 이고 (f(n)이 크다면), 충분히 큰 모든 n에 대해 $af(n/b)≤f(n)$이면,
 $T(n) = ⊝(f(n))$이다.
3. $f(n)/h(n)=⊝(1)$이면, $T(n)= ⊝(h(n) logn)$ 이다.

(예)

• $T(n) = 2T(n/3)+c$
  • a=2, b=3, h(n)=$n^(log_32)$, f(n)=c
  • $T(n) = ⊝(n^{log_32})$
    
    
• $T(n) = 2T(n/4)+n$
  • a=2, b=4, h(n)=$n^(log_42)=1/2$, f(n)=n
  • $T(n) = ⊝(n)$
    
    
• $T(n) = 2T(n/2)+n$
  • a=2, b=2, h(n)=$n^(log_22)=n$, f(n)=n
  • $T(n) = ⊝(nlogn)$