[알고리즘] 차수 (Order)

• 입력의 크기가 충분히 큰 경우도 효율적인 알고리즘을 찾기위해서는 점근적 분석 방식을 이용한다.

◼︎ O : Big O, 점근점 상한
◼︎ Ω : Omega, 점근적 하한
◼︎ ⊝ : Theta, order, O⋂Ω

대표적인 복잡도

$2^n > n^3 > n^2 > nlog_2n > n > log_2n$

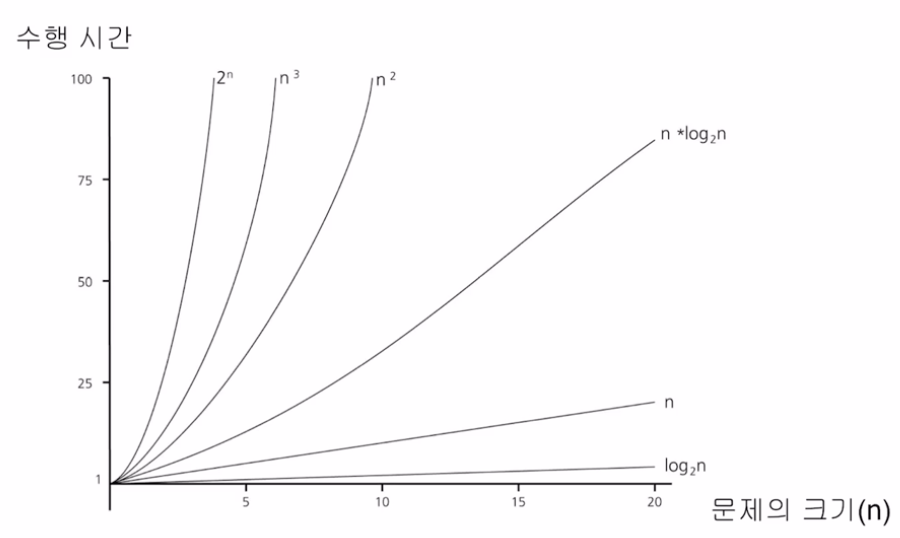
Big-O 표기법

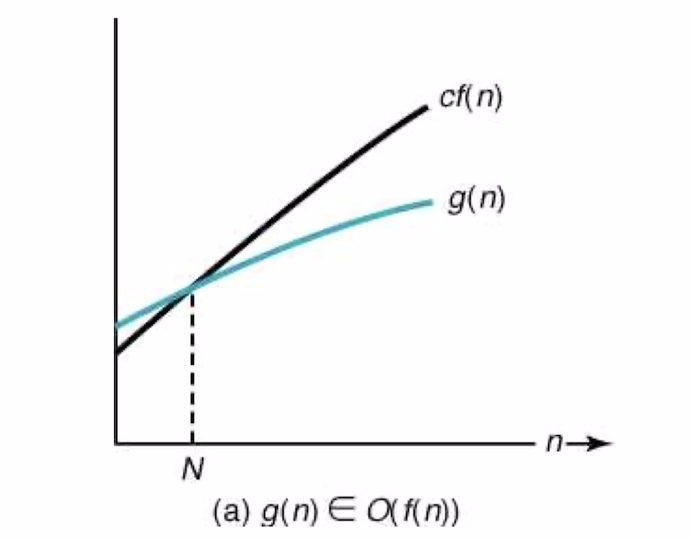
◼︎ 정의 : 주어진 복잡도 함수 f(n)에 대해서 g(n)∈O(f(n)) 이면 다음을 만족한다. (g(n): 분석된 결과)

n≥N인 모든 정수 n에 대해서 g(n)≤c*f(n)이 성립하는 실수 c>0와 음이 아닌 정수 N이 존재한다.

◼︎ 어떤 함수 g(n)이 O(f(n))에 속한다는 말은,
입력의 크기 n에 대해서 수행시간이 아무리 늦어도 f(n)은 된다. (f(n)이 상한이다.) 라고 말한다.
- 이 알고리즘의 수행시간은 f(n)보다 절대로 더 느릴 수는 없다.

Omega-표기법

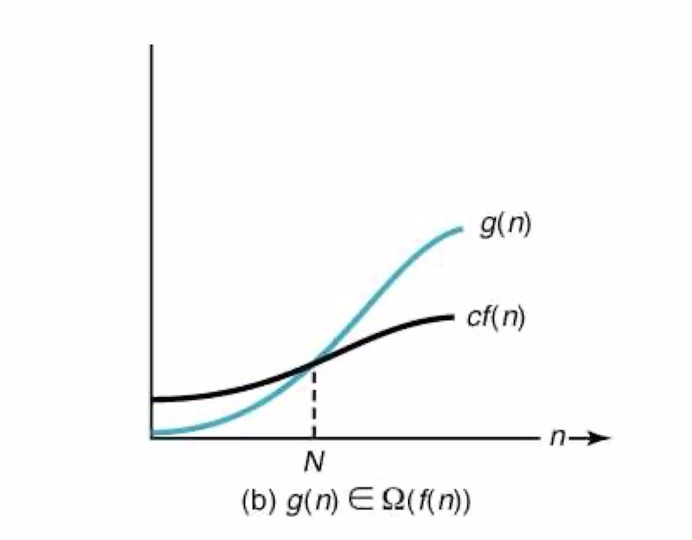
◼︎ 정의 : 주어진 복잡도 함수 f(n)에 대해서 g(n)∈Ω(f(n)) 이면 다음을 만족한다. (g(n): 분석된 결과)

n≥N인 모든 정수 n에 대해서 g(n)≥c*f(n)이 성립하는 실수 c>0와 음이 아닌 정수 N이 존재한다.

◼︎ 어떤 함수 g(n)이 Ω(f(n))에 속한다는 말은,
입력의 크기 n에 대해서 수행시간이 아무리 빨라도 f(n)밖에 되지 않는다. (f(n)이 하한이다.) 라고 말한다.
- 이 알고리즘의 수행시간은 f(n)보다 절대로 더 빠를 수는 없다.

Theta-표기법

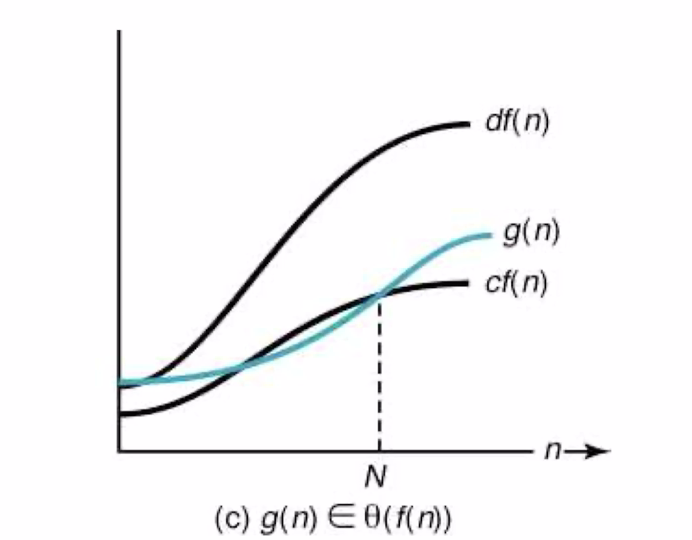
◼︎ 정의 : 주어진 복잡도 함수 f(n)에 대해서 ⊝(f(n) = O(g(n)) ⋂ Ω(f(n)) 이다.

n≥N인 모든 정수 n에 대해서 cf(n)≤g(n)≤df(n)이 성립하는 실수 c>0와 d>0, 그리고 음이 아닌 정수 N이 존재한다.