정렬
기초적인 정렬 알고리즘
- 평균적으로 의 시간이 소요되는 정렬 알고리즘들
- 선택정렬 (selection Sort)
- 버블정렬 (Bubble Sort)
- 삽입정렬 (Insertion Sort)
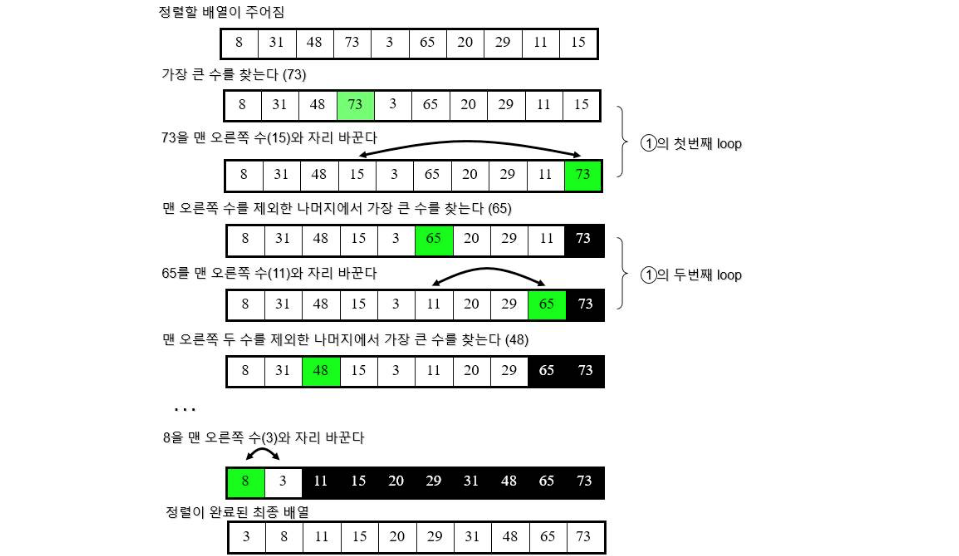
선택정렬 (Selection Sort)
- 각 루프마다
- 최대 원소를 찾는다.
- 최대 원소와 맨 오른쪽 원소를 교환한다.
- 맨 오른쪽 원소를 제외한다.
- 하나의 원소만 남을 때까지 위의 루프를 반복
재귀적 구조찾기

- 최대 원소를 찾고, 이를 맨 오른쪽 원소와 교환한다.
- 재귀적으로 이를 반복하는데 이때, 마지막 배열의 마지막 인덱스는 제외한 배열을 입력배열로 한다.
- 왜냐하면 마지막 인덱스는 이미 가장 큰 원소값으로 정렬되어있는 상태이므로 고려할 필요가 없기 때문
알고리즘

✓ 수행시간 :
➀ 의 for 루프는 n-1번 반복
➁ 에서 가장 큰 수를 찾기 위한 비교횟수 : n-1, n-2, ..., 2, 1
➂ 의 교환은 상수 시간 작업
작업 ➁가 가장 오랜시간이 걸리는 작업이다.
✔️ (n-1)+(n-2)+...+2+1 =
정렬 과정
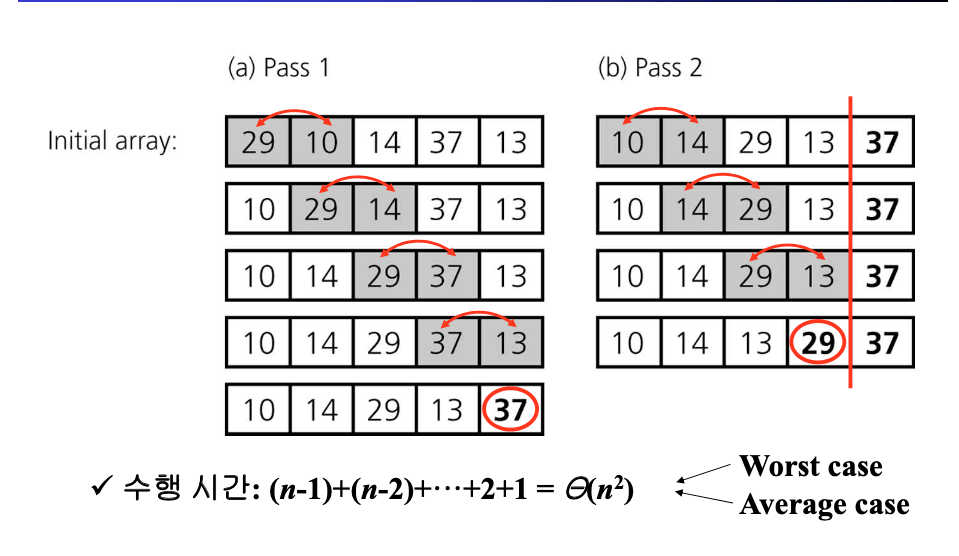
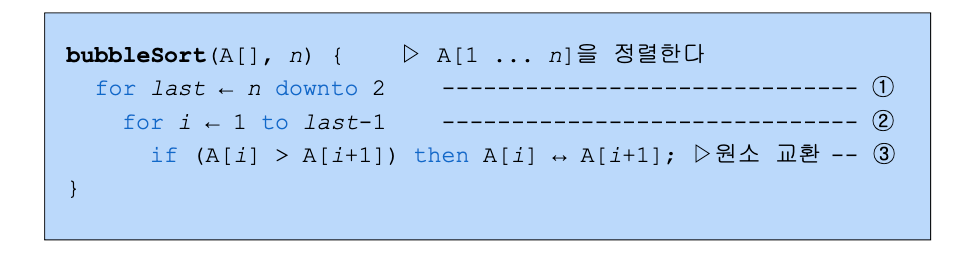
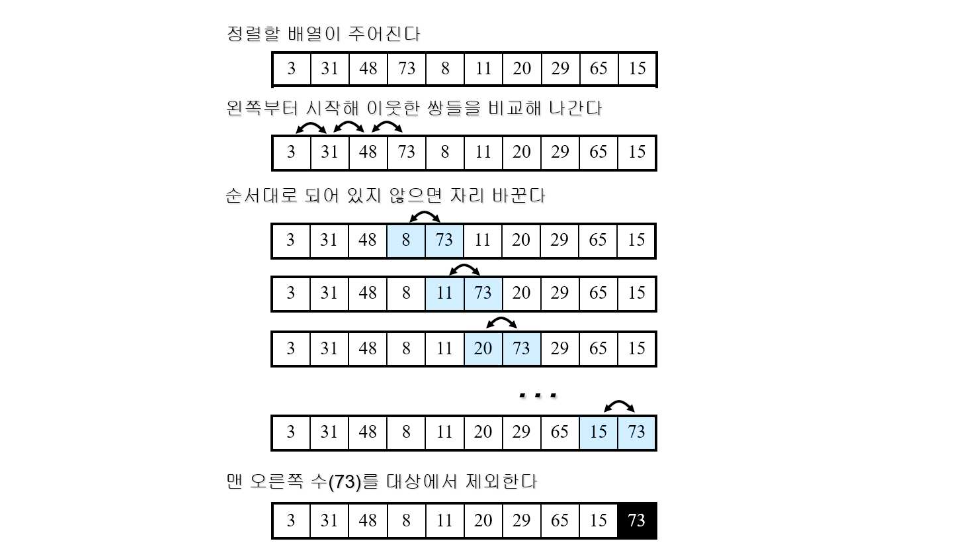
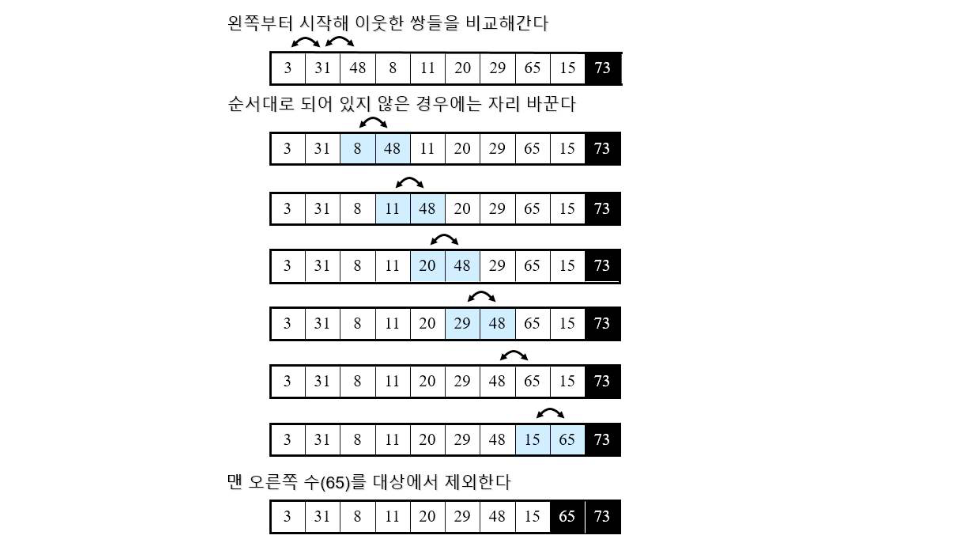
버블정렬 (Bubble Sort)
- 각 루프마다
- 이웃한 원소들간의 크기 비교
- 크기가 큰 원소가 좌측에 있다면, 원소를 교환
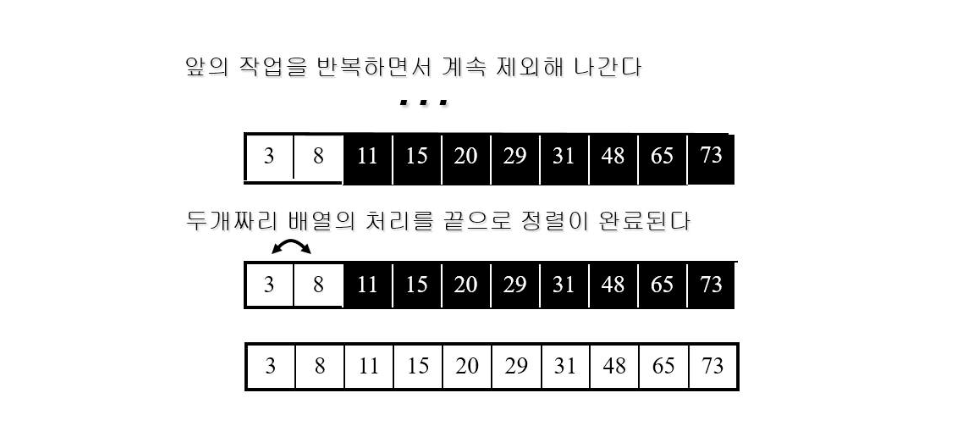
- 맨 오른쪽 원소를 제외한다.
- 하나의 원소만 남을 때까지 위의 루프를 반복
재귀적 구조찾기
- 최대 원소를 찾고, 이를 맨 오른쪽 원소와 교환한다.
- 재귀적으로 이를 반복하는데 이때, 마지막 배열의 마지막 인덱스는 제외한 배열을 입력배열로 한다.
- 왜냐하면 마지막 인덱스는 이미 가장 큰 원소값으로 정렬되어있는 상태이므로 고려할 필요가 없기 때문
알고리즘
✓ 수행시간 :
➀ 의 for 루프는 n-1번 반복
➁ 에서 가장 큰 수를 찾기 위한 비교횟수 : n-1, n-2, ..., 2, 1
➂ 의 교환은 상수 시간 작업
작업 ➁가 가장 오랜시간이 걸리는 작업이다.
✔️ (n-1)+(n-2)+...+2+1 =
정렬 과정
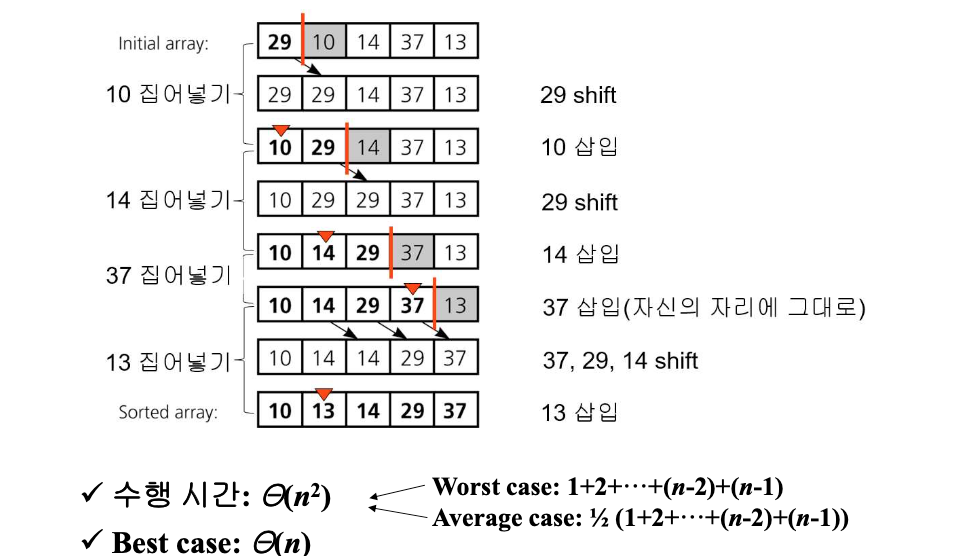
삽입정렬 (Insertion Sort)
- 각 루프마다
- 정렬되지 않은 원소를 하나 선택한다.
- 정렬된 원소들과 비교하여, 삽입될 적절한 위치를 탐색한다.
- 첫번째 선택시에는 정렬된 원소들이 없으므로 고려하지 않아도 된다.
- 적절한 위치를 발견하면, 기존의 원소를 shift하고 해당 위치에 삽입한다.
- 모든 원소가 정렬될 때까지 위 루프를 반복한다.
알고리즘

✓ 수행시간 :
➀ 의 for 루프는 n-1번 반복
➁ 의 삽입은 최악의 겨우 i-1회 비교
재귀호출이 아닌 반복문으로 구현한다.
✔️ Worst case :
✔️ Average case :
✔️ Best case : (#n-1번 반복)
고급 정렬 알고리즘
- 평균적으로 의 시간이 소요되는 정렬 알고리즘들
- 병합정렬 (Merge Sort)
- 퀵정렬 (Quick Sort)
- 힙정렬 (Heap Sort)
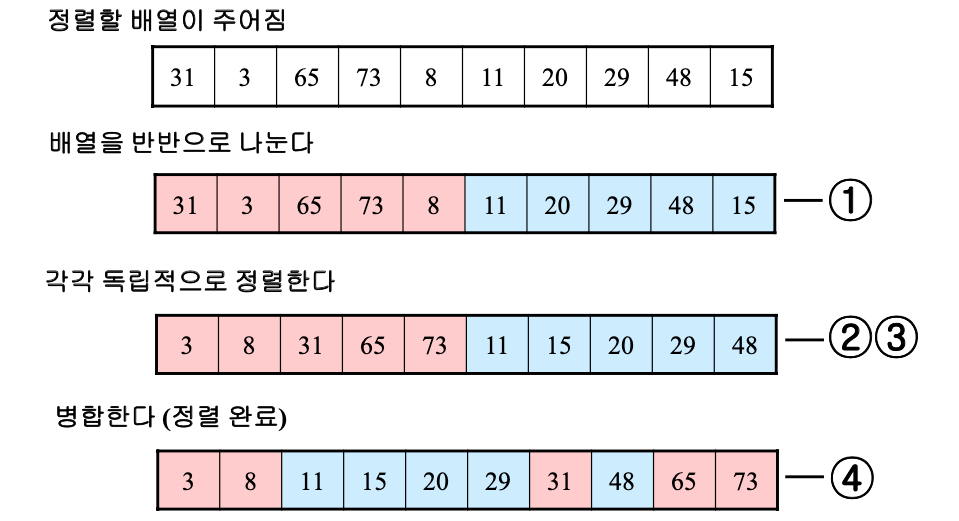
병합정렬
재귀적 구조찾기
- 주어진 배열을 반으로 나눈다.
- 나누어진 배열을 각각 독립적으로 정렬한다.
- 정렬을 마치면 나누었던 두 배열을 병합하면서 정렬한다.
- 위 동작을 재귀적으로 호출하여 전체 배열을 정렬한다.
알고리즘

정렬 과정
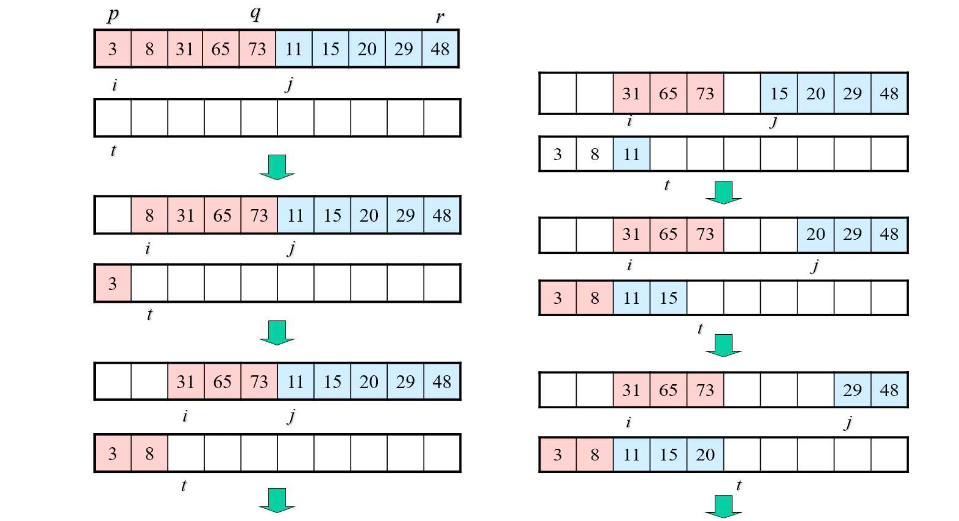
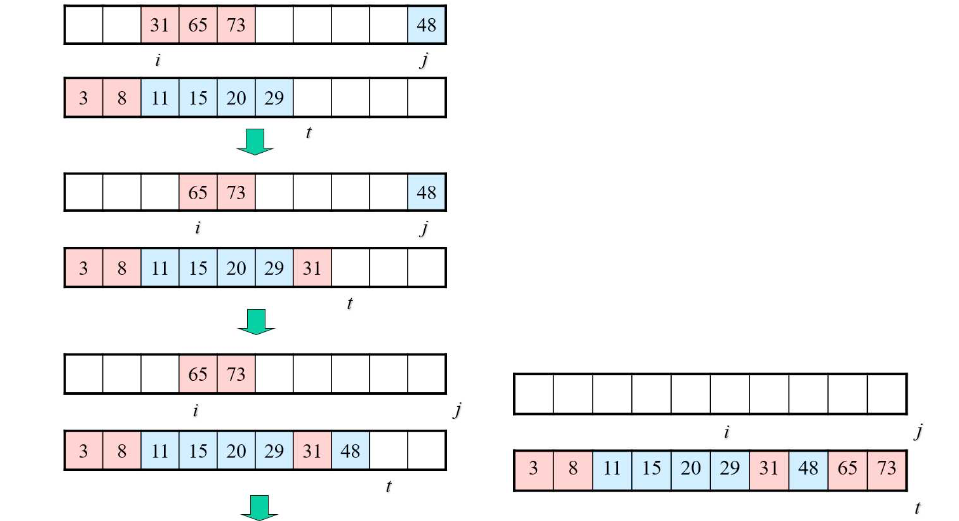
✔️ 수행 시간 :
퀵정렬
재귀적 구조찾기
- 기준 원소를 지정한다.
- 지정 원소를 기준으로 작은수는 왼쪽, 큰수는 오른쪽으로 분할한다.
- 위 동작을 재귀적으로 호출하여 왼쪽 배열을 정렬한다.
- 위 동작을 재귀적으로 호출하여 오른쪽 배열을 정렬한다.
알고리즘

정렬 과정

- 분할(partition) 과정

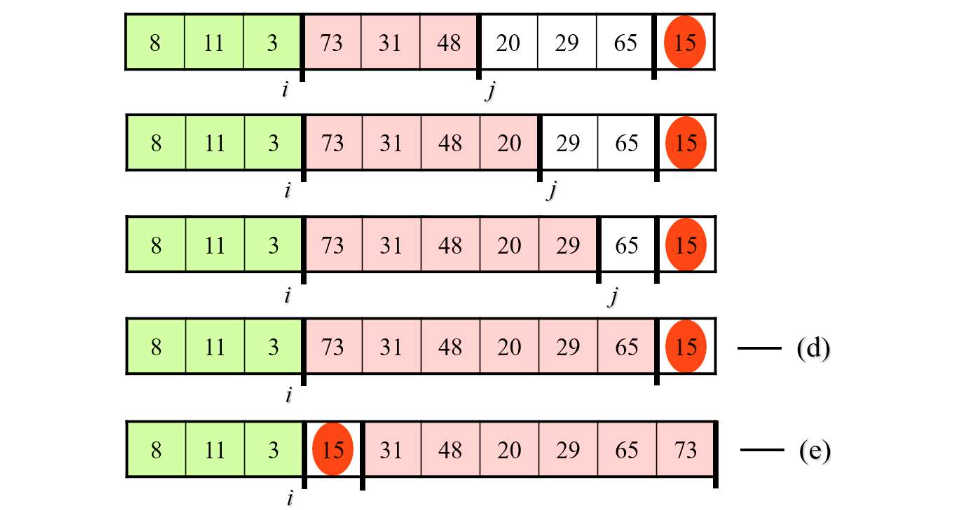
✔️ 수행 시간 :
힙 정렬
- 힙 (Heap)
: Complete binary tree로서 다음의 성질을 만족한다.- 각 노드의 값은 자신의 자식노드의 값보다 크지 않다.
- 힙정렬
: 주어진 배열을 힙으로 만든다음, 차례로 하나씩 힙에서 제거함으로써 정렬한다.
알고리즘

- buildHeap() 은 주어진 배열을 이용하여 힙을 만드는 함수이다.
- heapify() 는 현재 배열이 Heap의 성질을 만족하는지 확인하고, 만족하도록 원소를 교환하는 함수이다.
✔️ 최악의 경우에도 시간 소요!
배열을 이용한 힙 표현
- 힙은 배열을 이용해서 표현할 수 있다.
- i가 부모노드의 인덱스라면, 왼쪽 자식노드는 2i, 오른쪽 자식노드는 2i+1 로 표현 가능하다.
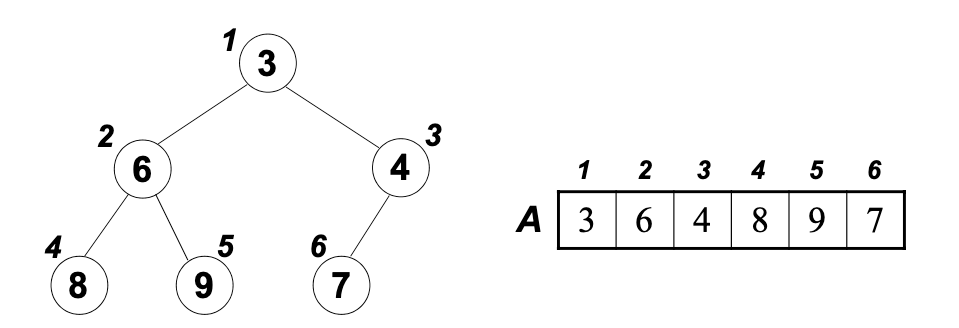
정렬 과정
-
주어진 배열을 이용하여 힙을 만든다.
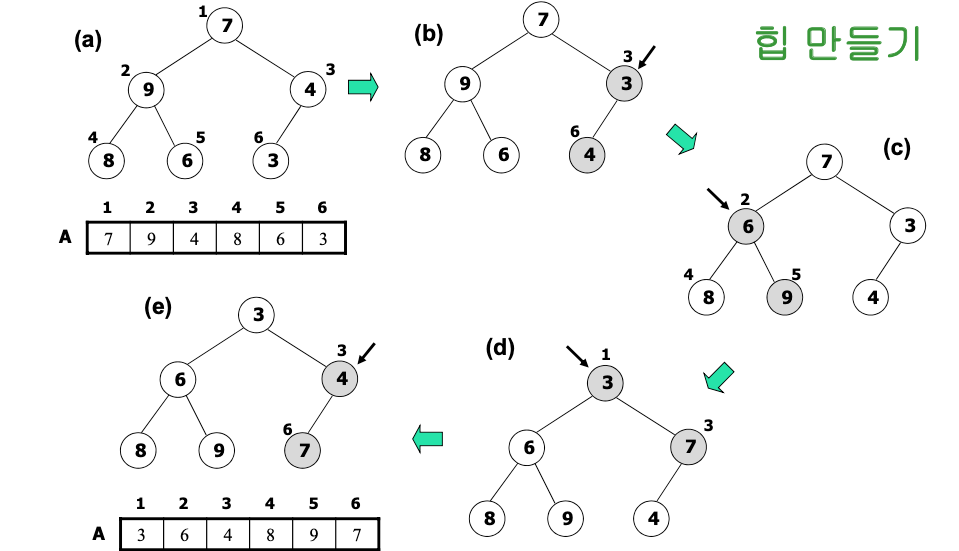
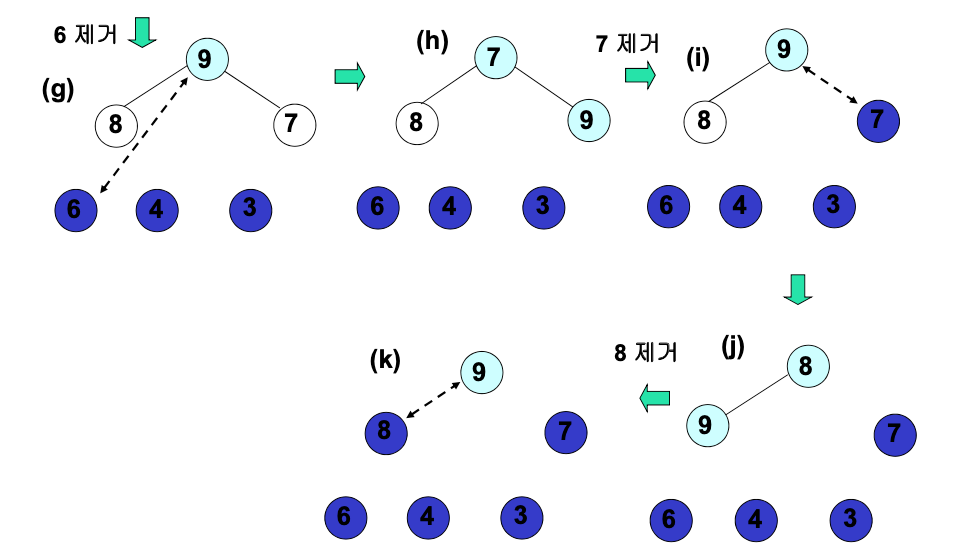
-
각 루프마다
- 첫번째 원소(가장 작은 원소)와 마지막 원소(가장 큰 원소)를 교환한다.
- 마지막 원소(가장 작은 원소)를 힙에서 제거한다.
- 힙의 성질을 만족하는 지 확인한다.
-
모든 원소가 힙에서 제거될 때까지 위 루프를 반복한다.

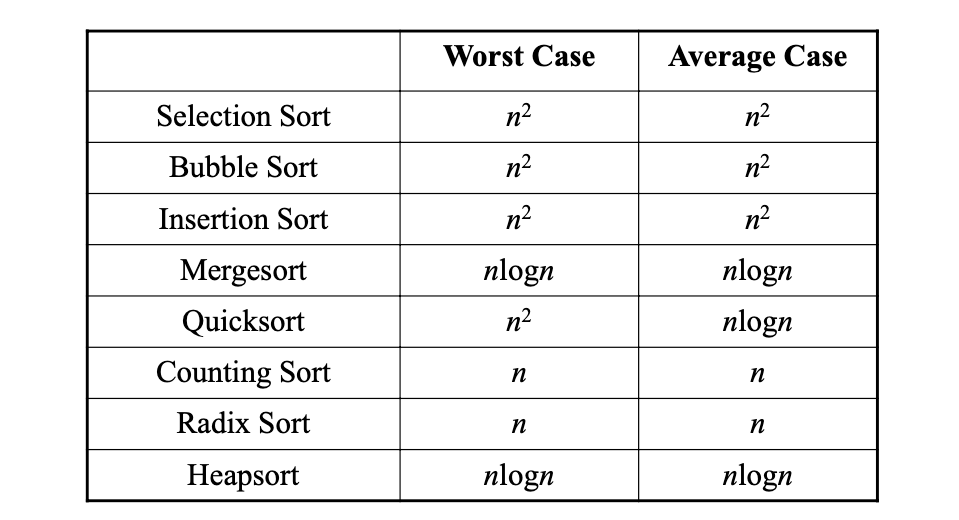
각 정렬방법의 시간 복잡도