[10week] 언어 지능 딥러닝

atdawn·2024년 11월 5일

AIVLE

목록 보기

20/25

TF-IDF : TermFrequency - Inverse Document Frequency

어떤 문서를 주며 핵심어를 추출해야 한다고 할때, 컴퓨터는

1. 많이 언급 되는 단어 (TF)
1. 그 중 이 문서에서만 등장하는 단어 (IDF)

를 기준으로 핵심어를 추출한다.

단어표현

컴퓨터는 단어를 벡터로 변환하여 모델에 적용한다.

One-Hot-Encoding : 기본

단어의 의미나 특성을 표현할 수 없음 : 자연어 처리에 적절하지 X
- 해당하는 클래스의 값만 1을 갖고 나머지는 모두 0의 값을 갖는다. : 저밀도
- 벡터 크기 = 1, 벡터간 각도 = 90' : cos90' = 0 이기 때문에 유사도를 측정할 수 X
- 단어 수가 매우 많으므로 고차원 저밀도 벡터를 구성하여 유사도를 측정하기 어려움

=> 차원을 낮추고 밀도를 높이는 방향의 방법을 고려해야 함!

벡터의 크기가 작으면서 단어의 의미를 표현하는 방법 : 분포 가설에 기반

딥러닝 기반의 유사도 판단

텍스트를 벡터화 한 후 벡터화된 각 문장 간의 유사도를 측정하는 방식
자카드 유사도, 코사인 유사도, 유클리디언 유사도, 맨하탄 유사도

자카드 유사도

두 문장을 각각 단어의 집합으로 만든 뒤 두 집합을 통해 유사도를 측정
자카드 유사도는 벡터화없이 유사도 측정 가능
측정법 : A/B
- A : 두 집합의 교집합인 공통된 단어의 개수
- B : 집합이 가지는 단어의 개수
0~1 사이의 값을 가짐

코사인 유사도

두 벡터 사이의 각도를 구하는 방법
-1~1 사이의 값
완전히 같을 때 (0) : 1의 값을 가짐
완전히 다를때 (180) : -1의 값을 가짐

유클리디언 유사도

두 벡터간의 거리로 유사도를 판단.
기준 : 유클리디언 거리 판단 ( 두 점 사이의 거리)

멘헤튼 유사도

두 벡터간의 거리로 유사도를 판단
기준 : 멘헤튼 거리 (수평 거리 + 수직 거리)

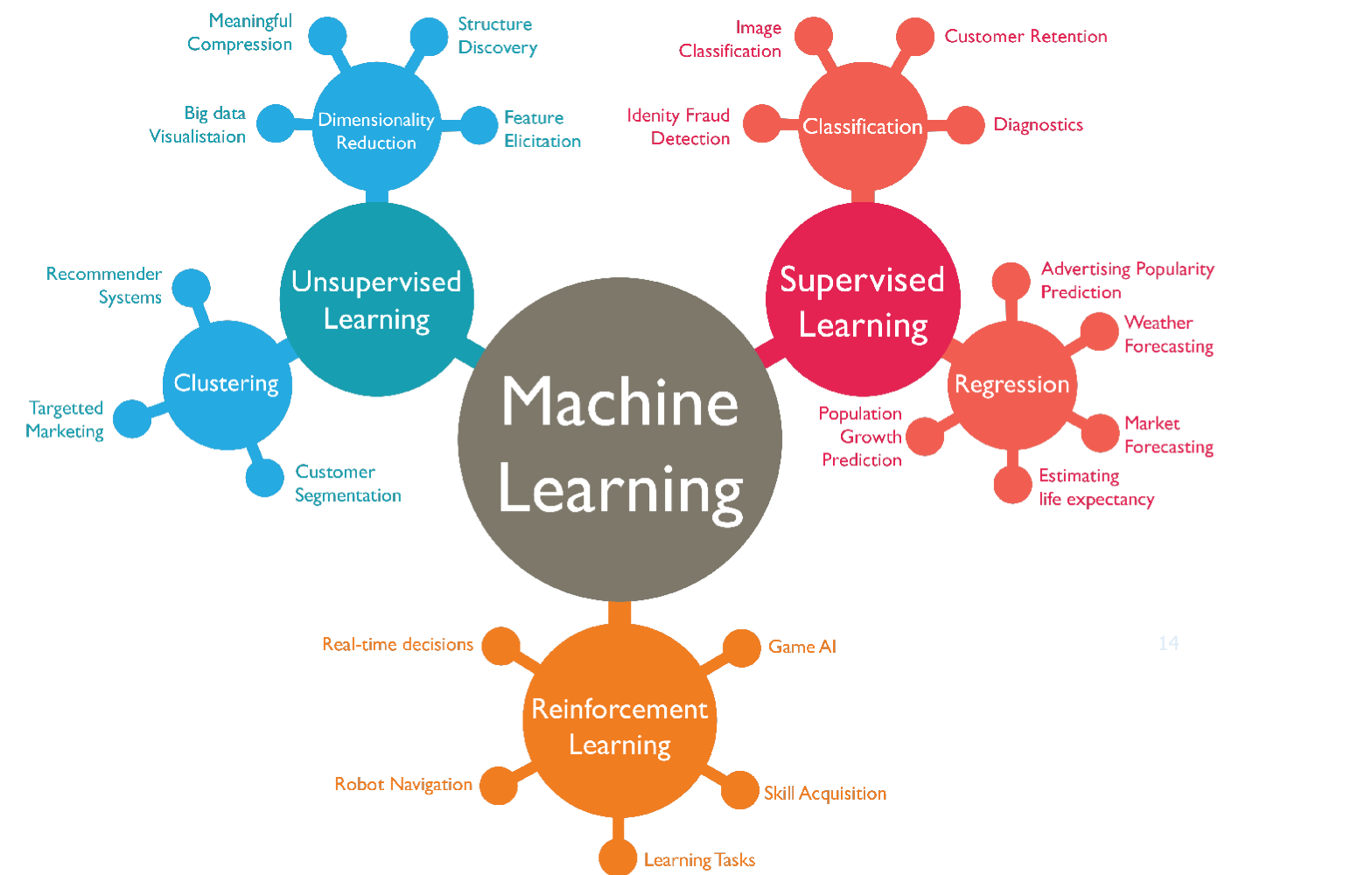
비지도 학습

데이터는 주어지나, 라벨이 주어지지 않음

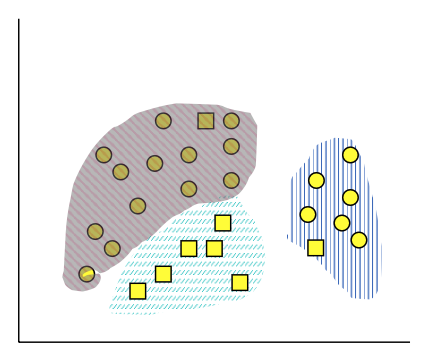
Clustering

레이블 없는 데이터를 모두 벡터로 만들고 비슷한 것들을 묶음
threshold 값에 따라 묶이는 범위가 다름
threshold는 사용자 정의 값
정답이라는 것은 존재하지 X

데이터 타입

이산형
연속형

데이터 표현

Data matrix (object-by-feature structure)

주로 각 데이터를 좌표로 나타냄
n 개의 데이터가 있을때, p 크기의 특징(Feature)을 가진다.

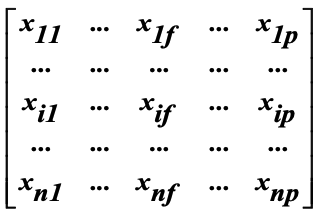
Distance/dissimilarity maxtrix (object-by-object structure)

데이터 간의 거리를 나타냄

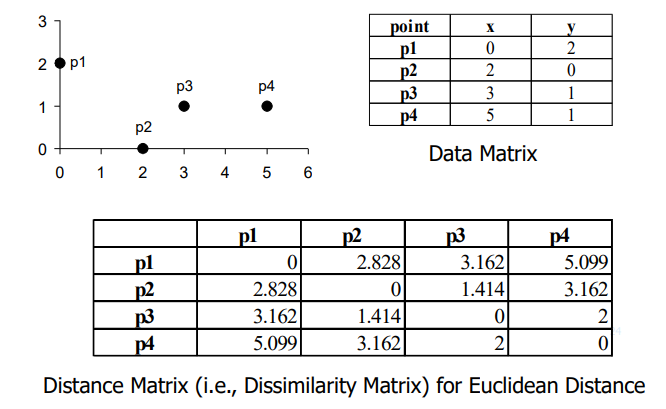
거리 측정 방법

민코프스키 거리 (Minkowski Distance)

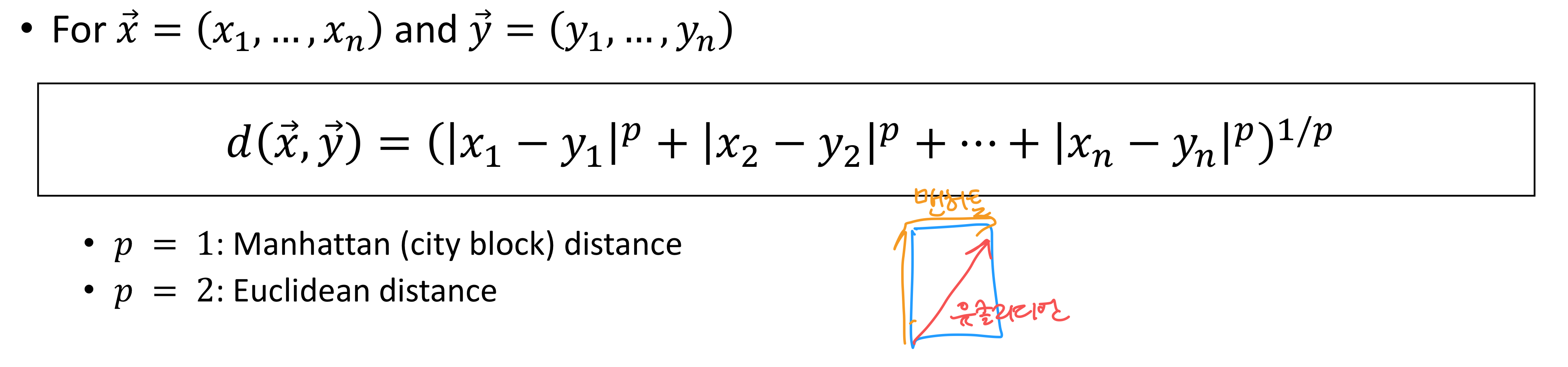
코사인 측정 (Cosine Measure)

벡터의 크기는 고려하지 않고 방향만 고려 (분모로 벡터 크기를 나누어줌)
cosine 범위 : -1 ~ +1
distance 범위 : 0 ~ 2

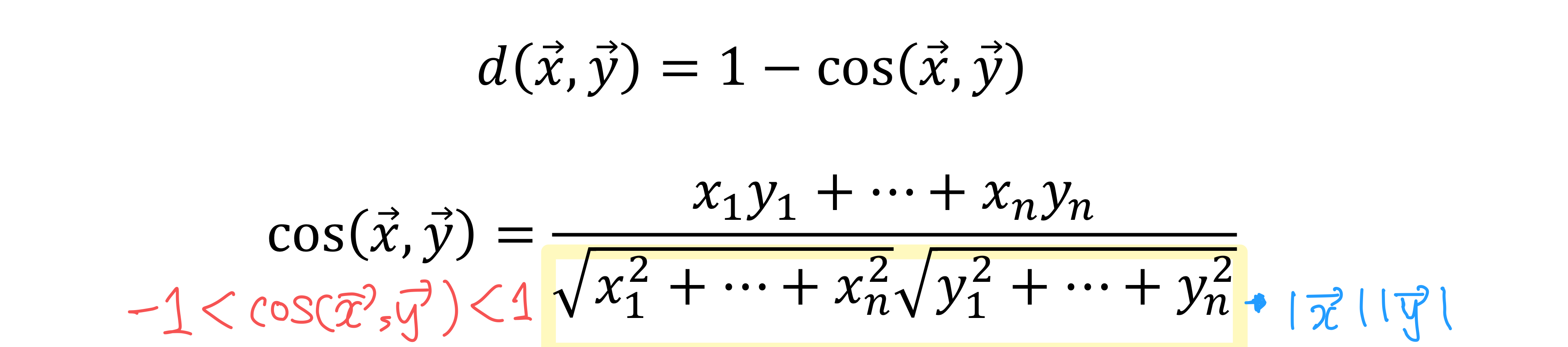
클러스터링 접근법

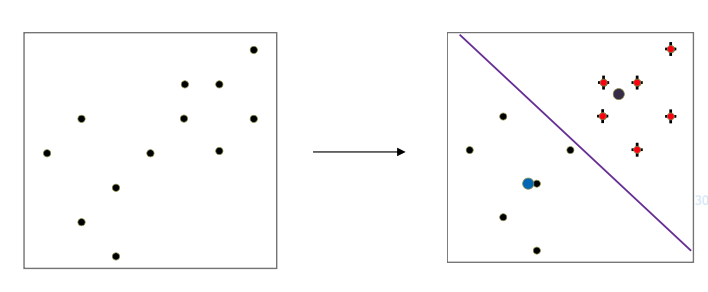
K-menas-clustering

K 개의 대표값을 랜덤으로 뽑는다.
이 대표값을 기준으로 클러스트링을 한다. ( 가까운 값을 같은 그룹으로 묶음)
각 집단의 평균 점을 구하고 그 점과 가장 가까운 데이터를 대표값으로 변경한다.
다시 클러스트링
클러스터링이 변화하지 않을 때 까지 반복

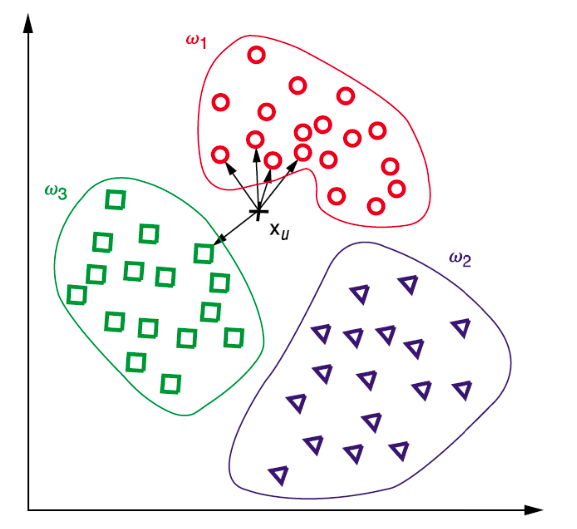
KNN (k Nearest Neighbor)

가장 가까운 이웃 k 개를 고름 -> 가장 많은 그룹에 묶음
k 값을 지정하는 것이 가장 중요

코드 실습

mport numpy as np

point = np.array([120,30])
k = 10

# 각 그룹의 샘플 수와 차원 설정
group_A = np.zeros((15, 2))  # 앞의 값은 샘플의 수, 뒤의 값은 샘플의 차원
group_B = np.zeros((15, 2))
group_C = np.zeros((15, 2))

# 각 그룹마다 랜덤값을 부여
group_A = np.random.uniform(100,200,size=(15,2)) # 100~200 실수값
group_B = np.random.uniform(0,50,size=(15,2)) # 0~50 실수값
group_C[:,0] = np.random.uniform(100,200,size=15) # x축은 100~100 실수값
group_C[:,1] = np.random.uniform(0,50,size=15) # y축은 0~50 실수값

# 두 점 사이의 유클리드 거리 계산 함수 정의
def distance(p, s):
    return np.sqrt(np.sum((p - s) ** 2))

distances = [] # 거리와 그룹 인덱스를 저장

# 각 그룹별로 거리 계산
for idx, group in enumerate([group_A, group_B, group_C]):
    for sample in group:
        distances.append((distance(point, sample), idx)) # (거리, 그룹 인덱스 ) 저장

# 거리에 따라 정렬
distances.sort(key=lambda x: x[0])

# k개의 가장 가까운 이웃 선택
nearest_neighbors = distances[:k]

# 각 그룹의 통계치를 나타내는 리스트
# 각 그룹에 해당하는 개수

stat = [0,0,0]

for neighbor in nearest_neighbors:
    group_index = neighbor[1]
    stat[group_index] += 1

# 이 stat 에서 최대로 큰 값의 위치를 구하면 그게 그룹이 됨
index = np.argmax(stat)

if index == 0:
    print("group A")
elif index == 1:
    print("group B")
else:
    print("group C")

Ensemble

클러스터링을 여러번 반복한 다음 취합 (k-means , knn 등등)

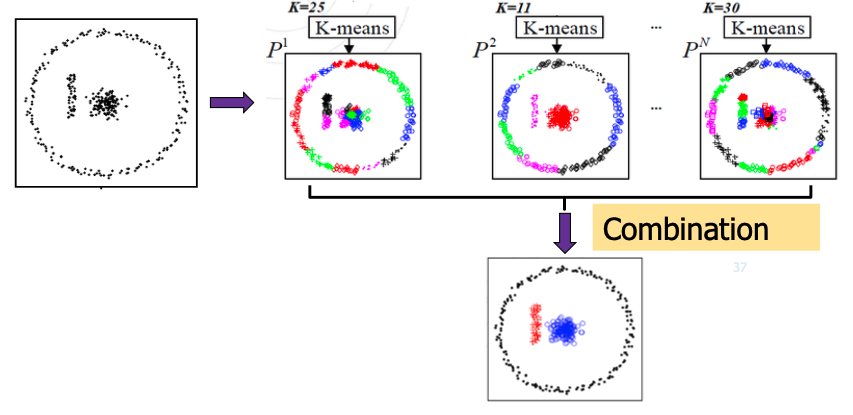
Word Embedding

단어들간의 관계를 나타내면서 단어를 벡터로 표현하는 방법
단어의 벡터는 이미 만들어서 라이브러리 형태로 제공 받음

Word2Vec : word to vector

word Embedding 알고리즘
텍스트를 벡터로 변환
원 핫 인코딩 을 사용하면서도 단어 간 유사도를 반영할 수 있도록 단어의 의미를 벡터화하는 방법이다.
비슷한 위치에서 등장하는 단어들은 비슷한 의미를 가진다는 분포 가설을 따르는 분산 표현 방법을 사용한다
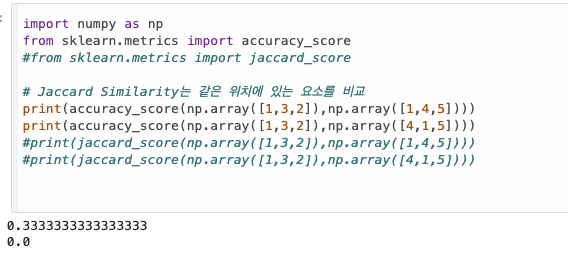
단점 : 원핫인코딩은 유사도를 가질 수 X
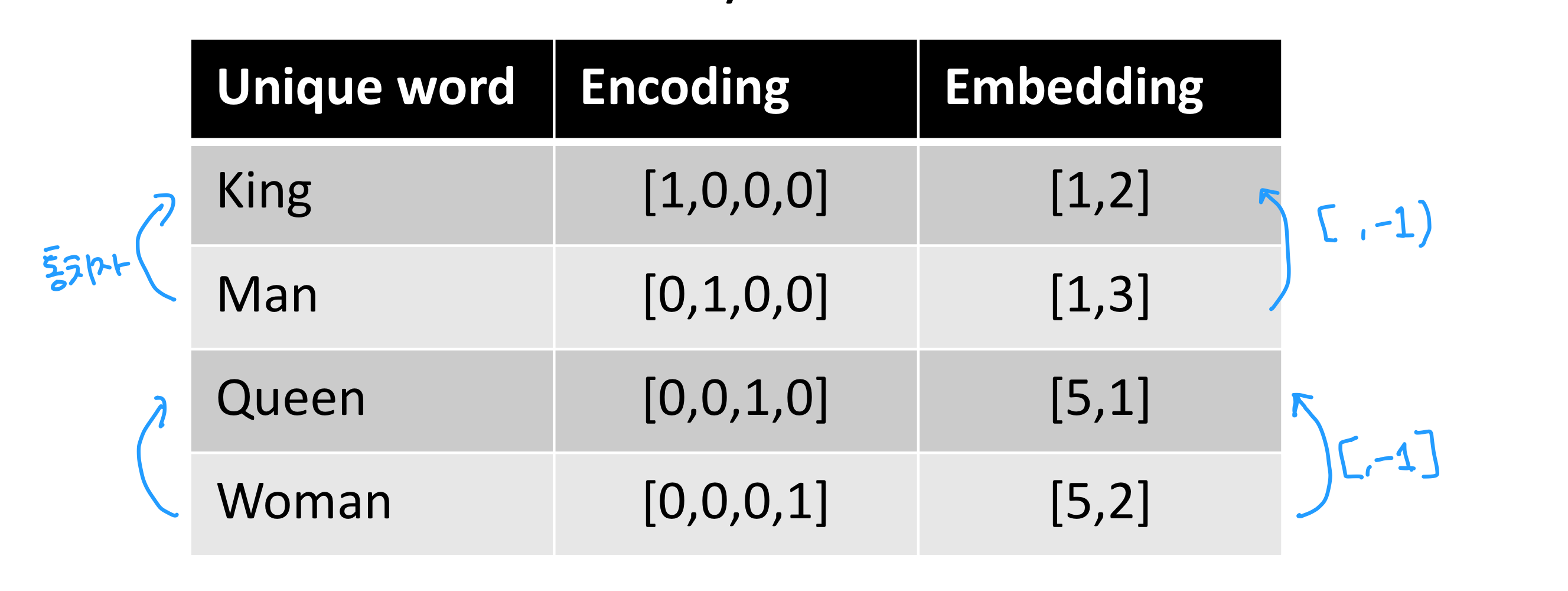
- 각 단어간 각도가 90도 이므로 코사인 유사도는 0을 가진다
위 예시처럼 통시자 속성을 부여하면 [,-1]을 하고, 여성 남성의 경우 [4,] 차이가 존재

+) skipgram : word2Vec data generation (Word2Vec 데이터를 만드는 과정)

중심 단어를 통해 주변에 있는 단어들을 예측하는 방법
중심 단어에 윈도우를 두고, 윈도우 내의 주변 단어의 임베딩 벡터를 예측

ex)

King brave man
Queen Beautiful Woman
window size = 2
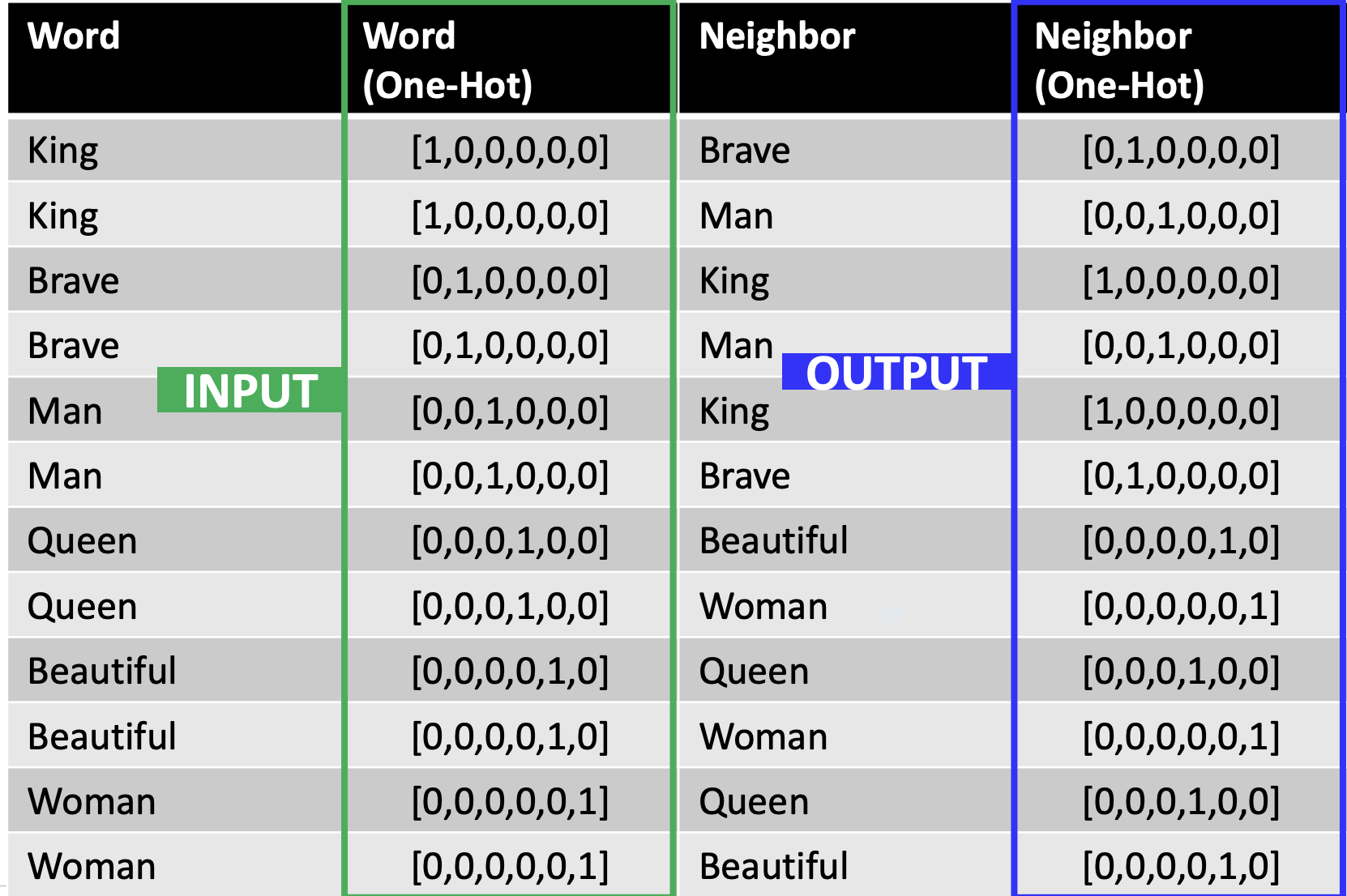
이렇게 나온 input 과 output을 신경망에 넣음.

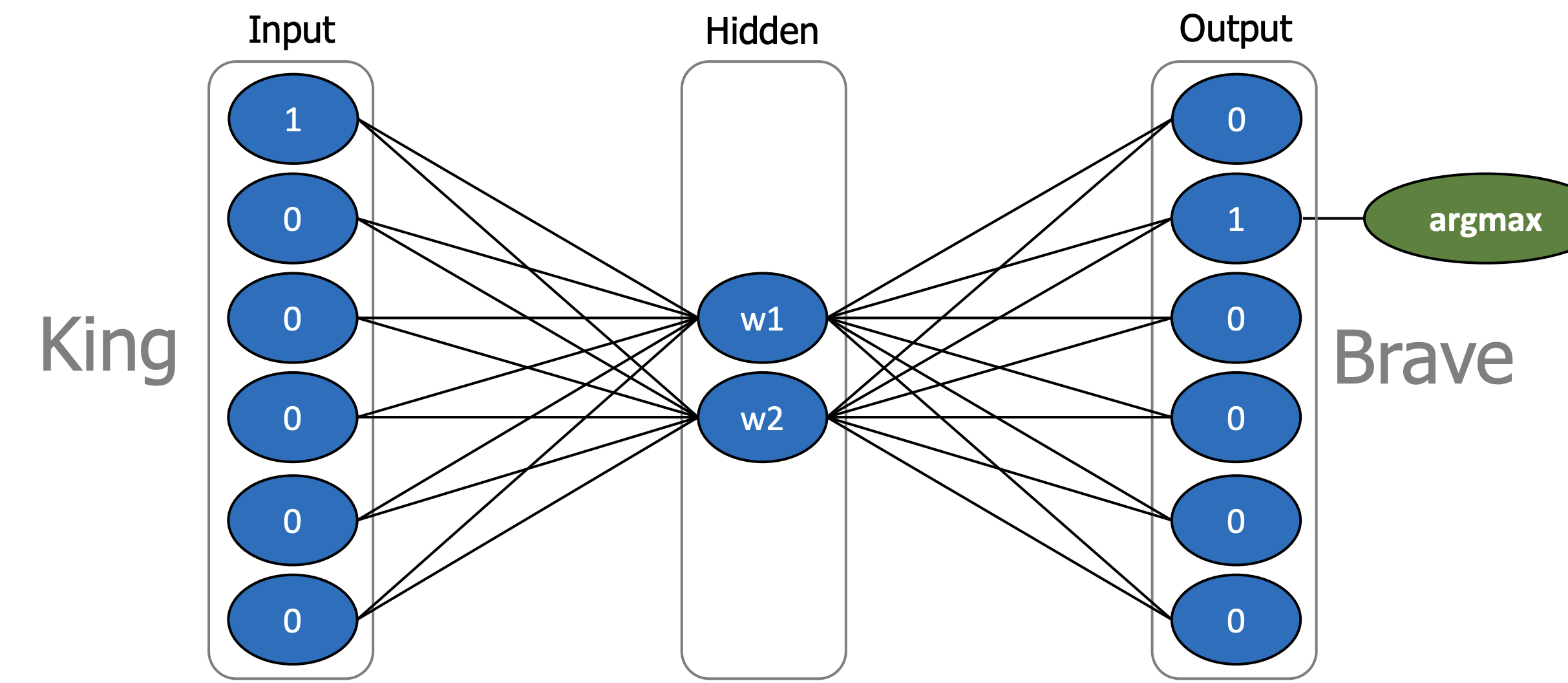
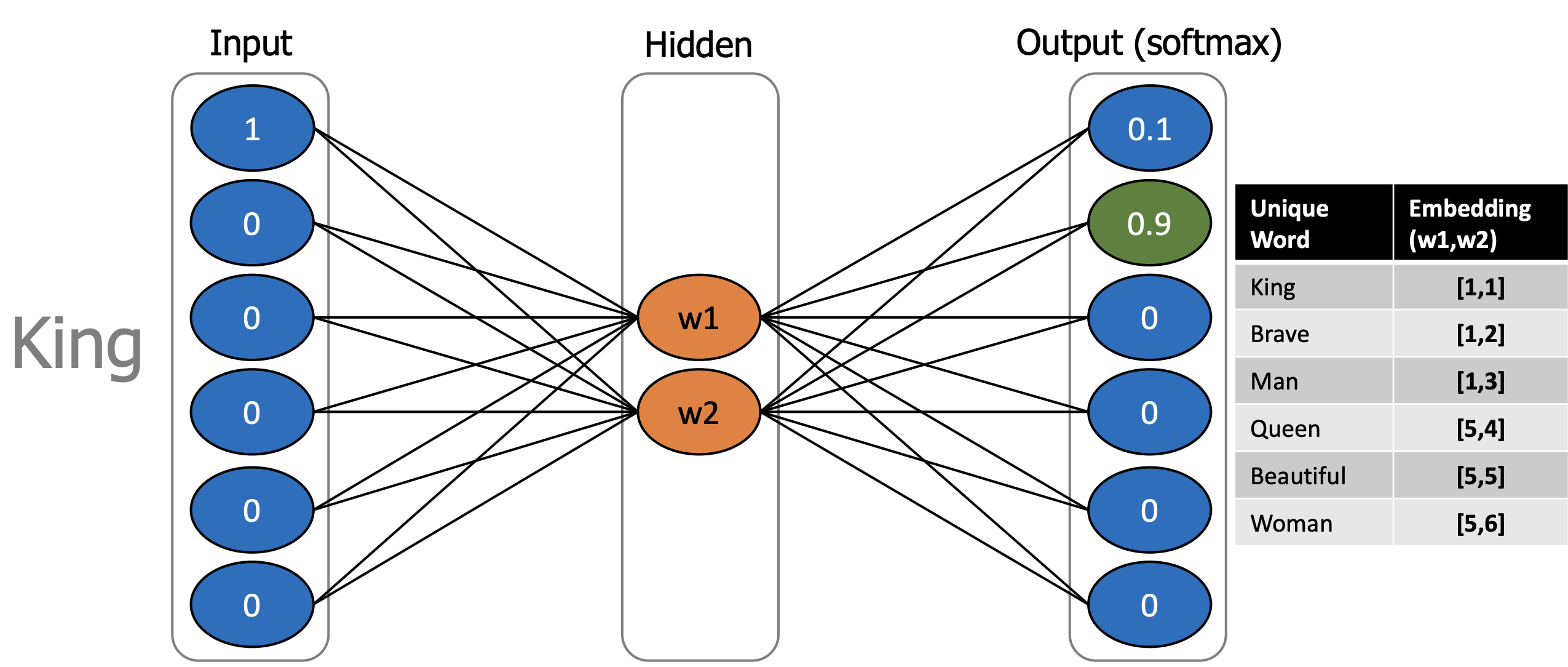
신경망을 통해 임베딩된 값을 뽑아냄.

정보검색, 추천 시스템

정보 검색

RSS 실습 : 깃허브 복습!

영화 리뷰기반 분석 실습 : 깃허브 복습!

언어 지능 인공 신경망

Linear Function

Linear Regression

선형으로 경향성을 판단
실제값과 모델값의 차이가 가장 적은 것이 좋은 모델
Learning rate를 적절히 조절하는 것이 중요

$H(x) = Wx + b$

W : 가중치
b : 절편
Feature와 각각의 가중치를 곱함

Cost Function (Loss Function)

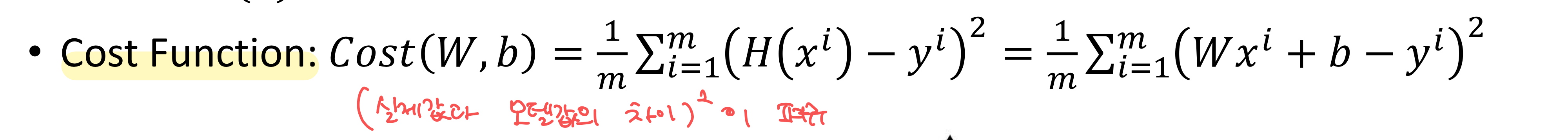
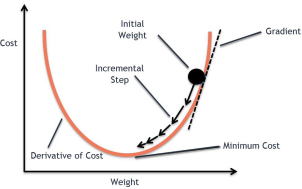
Cost 함수를 미분했을 때, 기울기가 크면, W를 크게 업데이트. 작으면 조금씩 업데이트

pytorch 실습

import torch

x_train = torch.FloatTensor([[1,1],[2,2],[3,3]])
y_train = torch.FloatTensor([[10],[20],[30]])
W = torch.randn([2,1], requires_grad=True) # 정규분포에 따른 난수를 반환: 차원크기, 생성되는 텐서의 기울기를 계산할 지 여부
b = torch.randn([1], requires_grad=True)
optimizer = torch.optim.SGD([W,b], lr=0.01)

# [딥러닝 1단계] 모델을 만든다. Model Setup
def H(x):
  model = torch.matmul(x,W)+b # matmul : 행렬 곱
  return model

# [딥러닝 2단계] 학습을 시킨다. Training
for iter in range(2000):
  cost = torch.mean((H(x_train)-y_train)**2) # 오차 제곱 평균 : 코스트 함수
  optimizer.zero_grad() # 이전 학습 스텝에서 계산된 gradient를 0으로 초기화 : gradient가 누적되지 않도록 하기 위함
  cost.backward() # w와 b에 대한 gradient를 계산
  optimizer.step() # 저장된 gradient를 사용하여 w와 b를 업데이트
  if iter%100 == 0 : print('[Iteration]',iter,'[Cost]',cost.detach().item())

# [딥러닝 3단계] 추론을 수행한다. Inference
x_test = torch.FloatTensor([4,4])
model_result=H(x_test)
print('Model Inference with [4,4]',model_result.detach().item())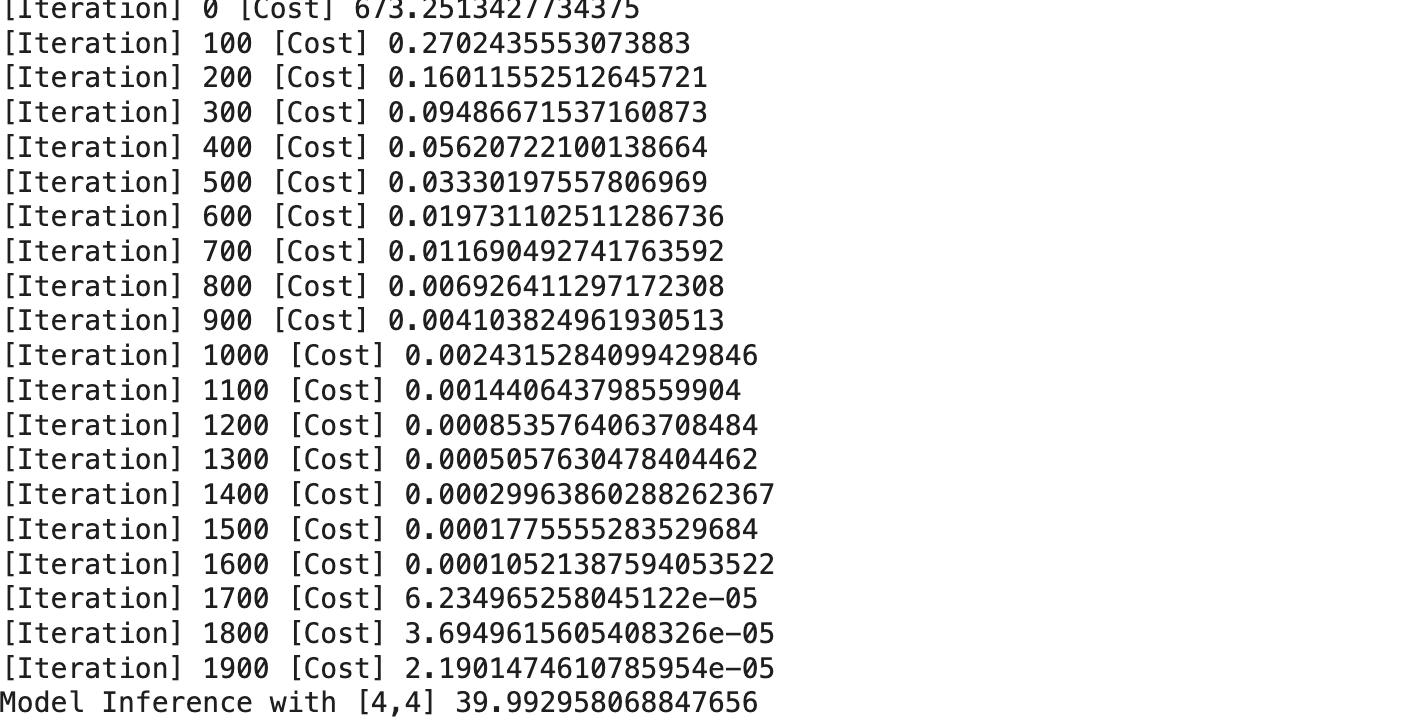

Binary Classification

1. Linear Regression으로 결과값을 추출
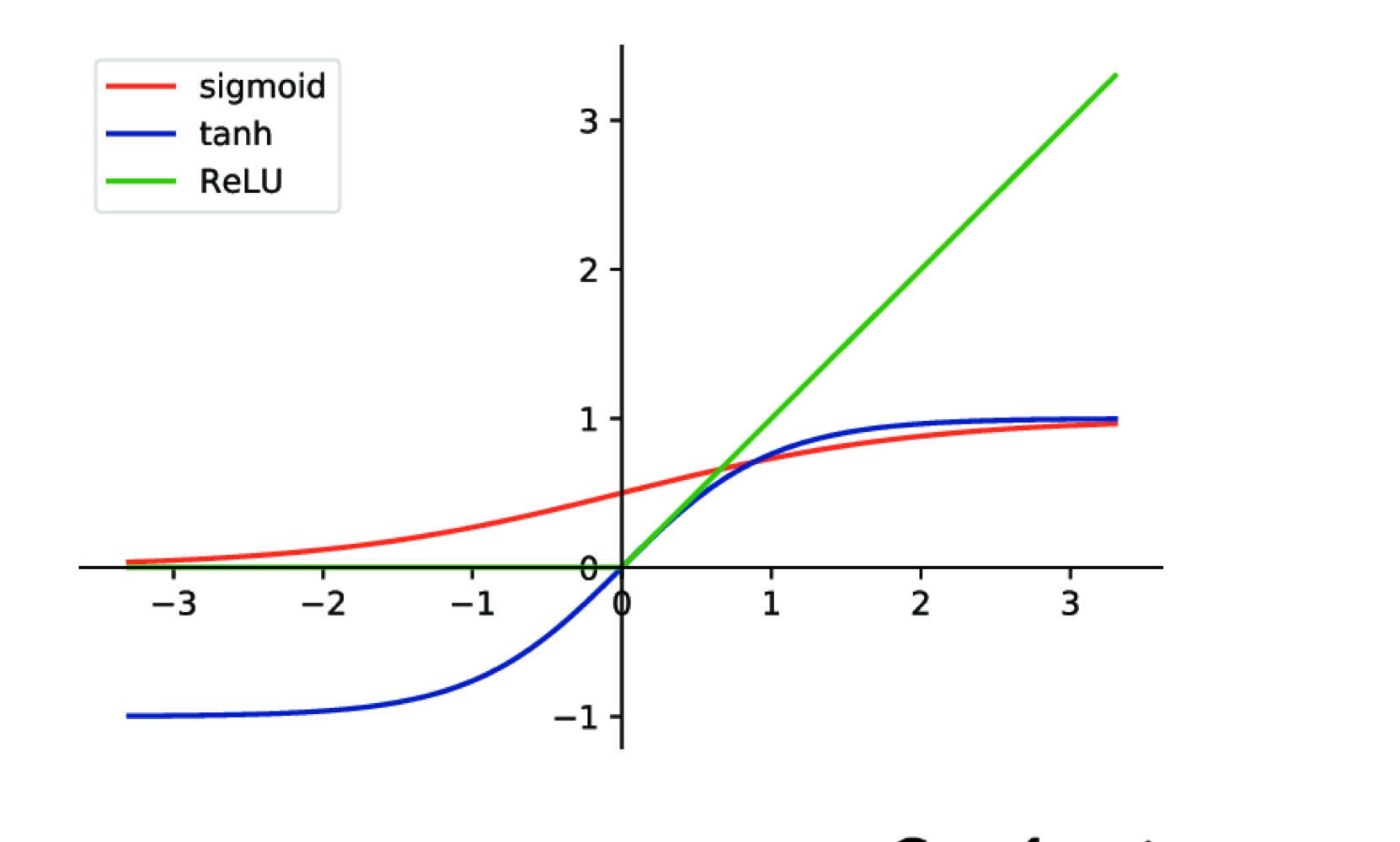
1. sigmoid function을 사용하여 0~1의 값으로 변환

Cost Function (Loss Function)

sigmoid 함수를 거치면 직선이 아니기 때문에 2차 함수가 나오지 않는다. -> 원래의 cost 함수를 사용하면 최적의 가중치를 얻는것이 불가능
=> 로그 함수를 사용하자!

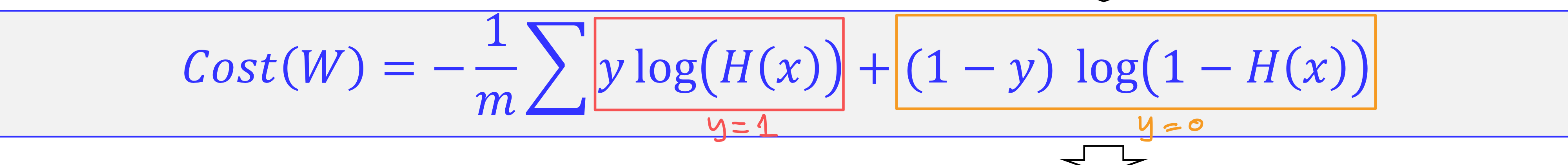
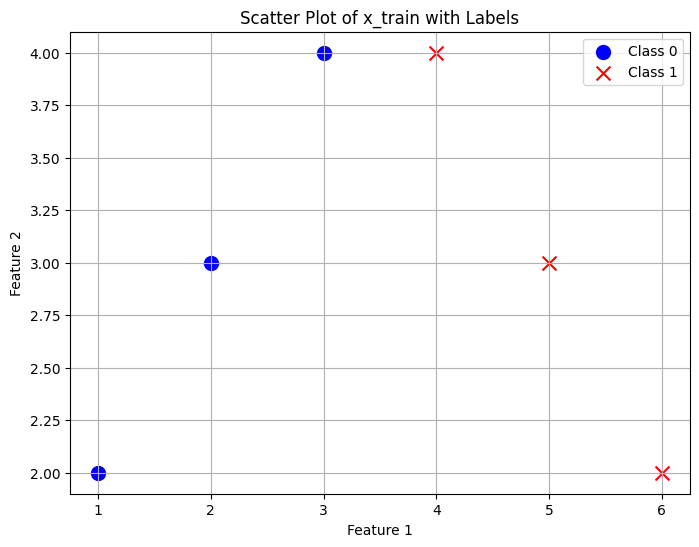
pytorch 실습

import torch

x_train = torch.FloatTensor([[1,2],[2,3],[3,4],[4,4],[5,3],[6,2]])
y_train = torch.FloatTensor([[0],[0],[0],[1],[1],[1]])
W = torch.randn([2,1], requires_grad=True) # 정규분포에 따른 난수를 반환: 차원크기, 생성되는 텐서의 기울기를 계산할 지 여부
b = torch.randn([1], requires_grad=True)
optimizer = torch.optim.SGD([W,b], lr=0.01)

# [딥러닝 1단계] 모델을 만든다. Model Setup
def H(x):
  model = torch.sigmoid(torch.matmul(x,W)+b) # matmul : 행렬 곱, sigmoid 함수로 0~1 값으로 변환
  return model

# [딥러닝 2단계] 학습을 시킨다. Training
for iter in range(2000):
  cost = torch.mean((-1)*y_train*torch.log(H(x_train))+(-1)*(1-y_train)*torch.log(1-H(x_train))) # 오차 제곱 평균 : 코스트 함수
  optimizer.zero_grad() # 이전 학습 스텝에서 계산된 gradient를 0으로 초기화 : gradient가 누적되지 않도록 하기 위함
  cost.backward() # w와 b에 대한 gradient를 계산
  optimizer.step() # 저장된 gradient를 사용하여 w와 b를 업데이트
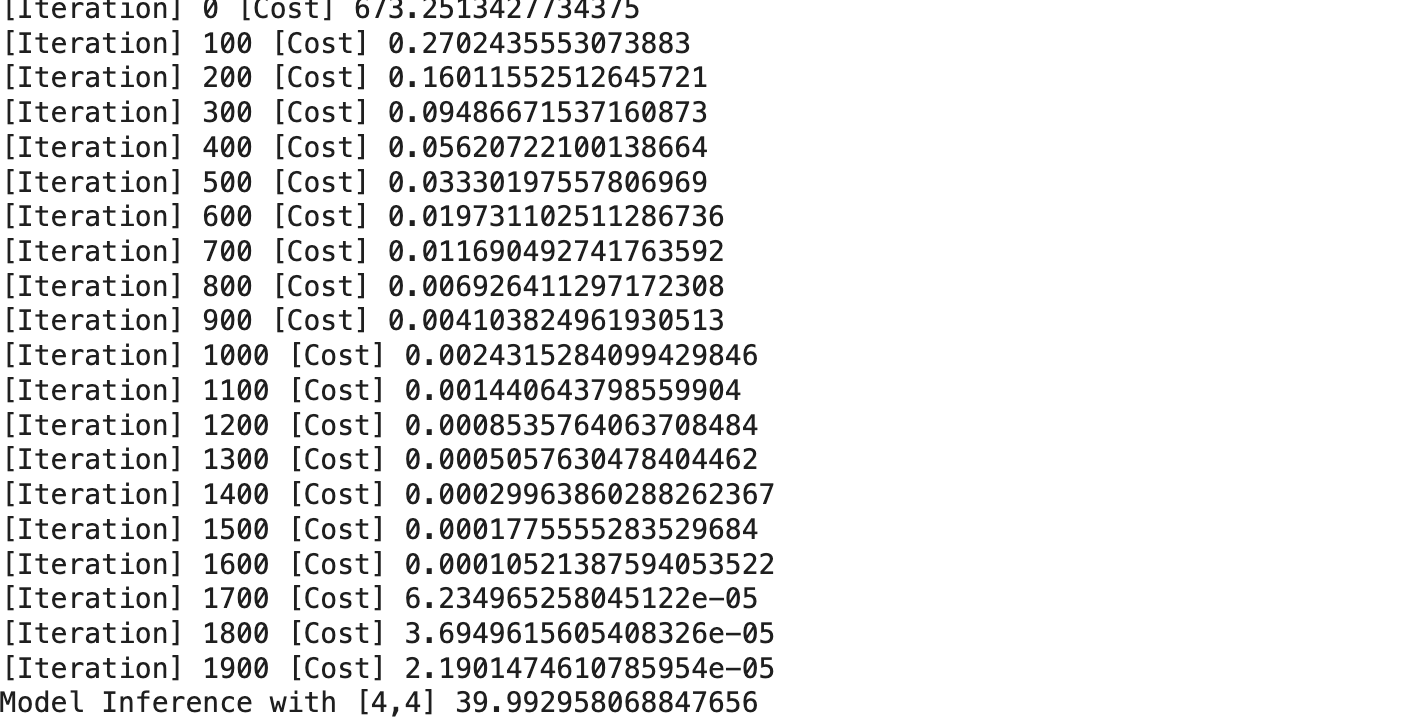
  if iter%100 == 0 : print('[Iteration]',iter,'[Cost]',cost.detach().item())

# [딥러닝 3단계] 추론을 수행한다. Inference
x_test = torch.FloatTensor([7,1])
model_result=H(x_test)
print('Model Inference with [7,1]',model_result.detach().item())
if model_result.detach().item() >= 0.5 : print('Pass')
else : print('Fail')

Softmax

다중 분류 모델
이진 분류를 여러번 반복하여 분류함
ex ) A야 아니야?, B야 아니야? , C야 아니야?
각 class일 확률이 저장되는데, argmax값을 구하면 된다.
softmax 에서 y값은 항상 one-hot-Encodding이 되어 있어야 한다.

Cost Function : Cross Entropy

$C(S,L) = - \Sigma L_i log(S_i)$

Nonlinear Functions

신경망 NN : Neural Network

히든 레이어를 추가하여 선 하나로 나뉘지 않는 문제를 해결 :XOR 문제
정교한 분류가 가능

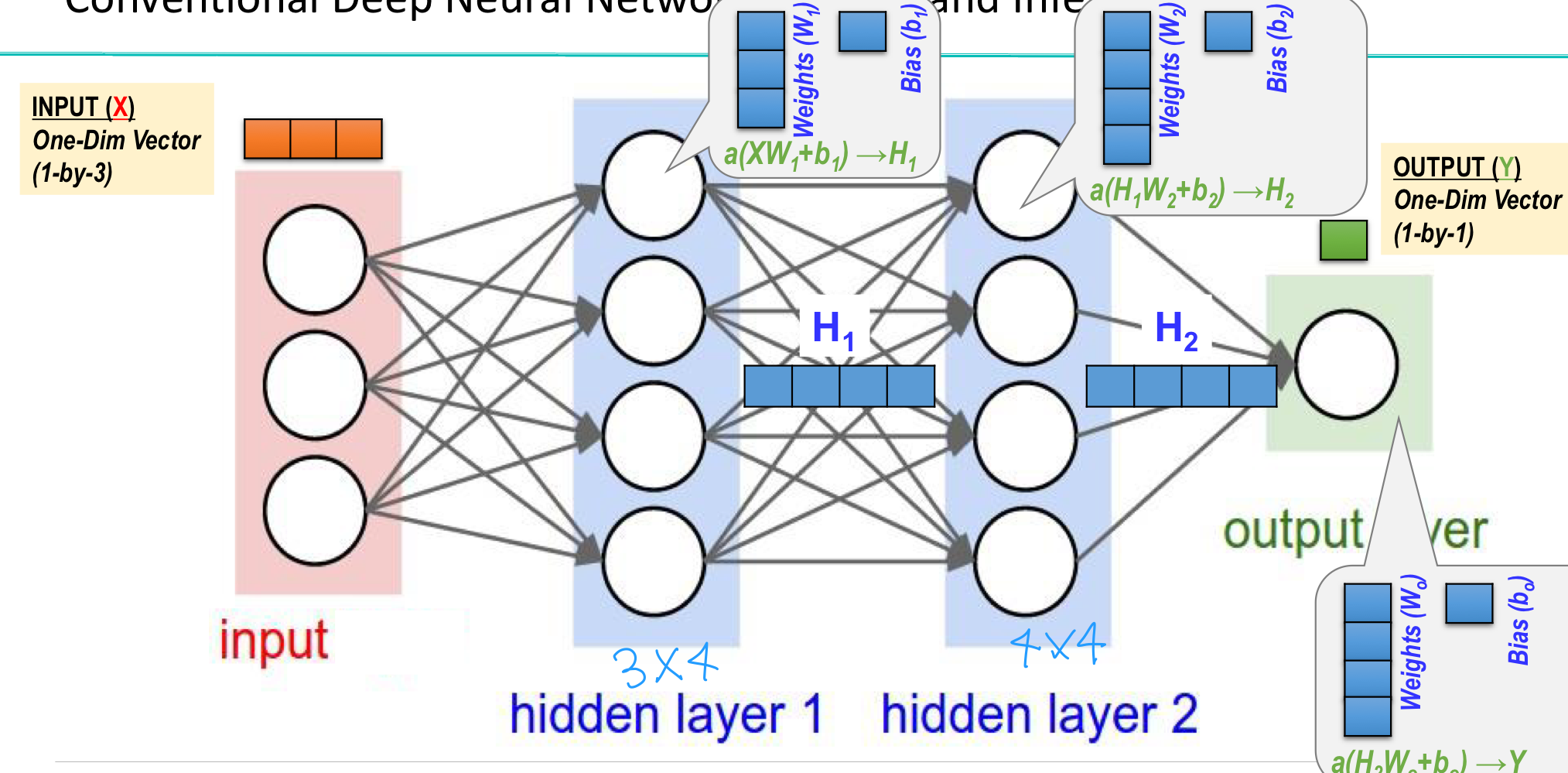
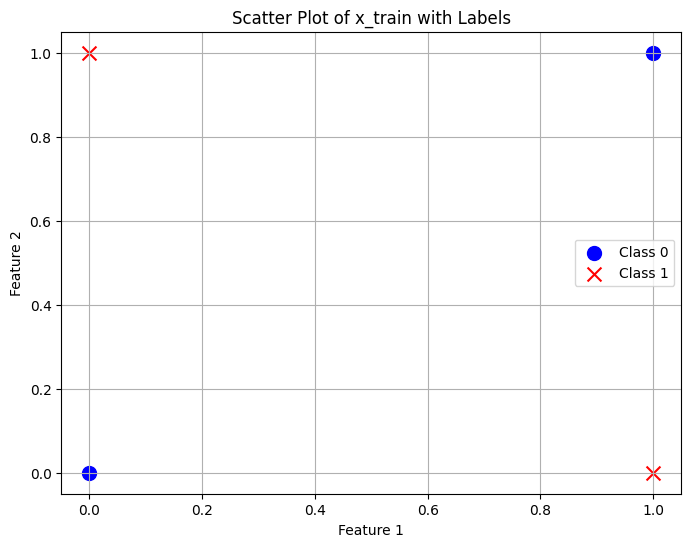
XOR 문제 해결

# hidden layer O
import torch

x_train = torch.FloatTensor([[0,0],[0,1],[1,0],[1,1]])
y_train = torch.FloatTensor([[0],[1],[1],[0]])
W_h = torch.randn([2,3],requires_grad=True) #hidden
b_h = torch.randn([3],requires_grad=True) #hidden
W_o = torch.randn([3,1],requires_grad=True) #ouput
b_o = torch.randn([1], requires_grad=True) #ouput
optimizer = torch.optim.SGD([W_h,b_h,W_o,b_o], lr=0.01)

# [딥러닝 1단계] 모델을 만든다. Model Setup
def H(x):
  HL1 = torch.sigmoid(torch.matmul(x,W_h)+b_h) # 히든 레이어 행렬 곱
  Out = torch.sigmoid(torch.matmul(HL1,W_o)+b_o) # 아웃풋 레이어 행렬 곱
  return Out

# [딥러닝 2단계] 학습을 시킨다. Training
for iter in range(200000):
  cost = torch.mean((-1)*y_train*torch.log(H(x_train))+(-1)*(1-y_train)*torch.log(1-H(x_train))) # 오차 제곱 평균 : 코스트 함수
  optimizer.zero_grad() # 이전 학습 스텝에서 계산된 gradient를 0으로 초기화 : gradient가 누적되지 않도록 하기 위함
  cost.backward() # w와 b에 대한 gradient를 계산
  optimizer.step() # 저장된 gradient를 사용하여 w와 b를 업데이트
  if iter%10000 == 0 : print('[Iteration]',iter,'[Cost]',cost.detach().item())

# [딥러닝 3단계] 추론을 수행한다. Inference
model_result=H(x_train)
print(model_result)

tensor(
[[0.0011],
[0.9924],
[0.9915],
[0.0122]], grad_fn=<SigmoidBackward0>)

ANN : ReLU(Rectified Linear Unit)

입력 값이 양수일때는 그대로, 음수일때는 0 출력
시그모이드 함수를 사용하면, layer을 깊이 쌓을 수록 기울기가 소실되는 문제가 발생
ReLU는 양수 구간에서는 기울기 값이 1로 유지되므로, 역전파 과정에서 기울기 소실 문제를 완화

$f(x) = max(0,x)$

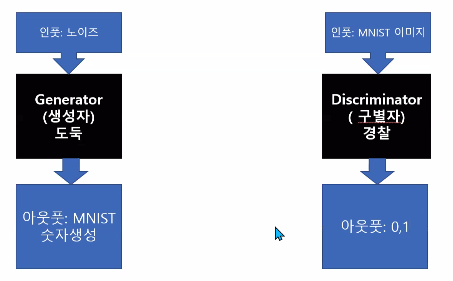
GAN : Generative Adversarial Networks

생성 모델

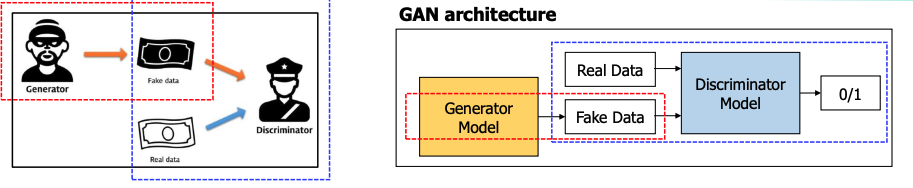
Generator(생성모델)와 Discriminator(분류모델)가 서로 경쟁하며 학습하여 점점 더 정교한 가짜 데이터를 생성하는 모델
Discriminator
Discriminator는 주어진 데이터가 진짜인지 가짜인지 분류하는 역할.
학습 초반에는 실제 데이터를 "진짜"로 분류하는 데 집중하며, Discriminator의 성능을 높임.
이후 Generator가 생성한 가짜 데이터를 "가짜"로 분류하도록 훈련.
Generator
input은 랜덤한 노이즈 값 (실제 데이터는 본적 없음)
Generator는 Discriminator를 속이는 방향으로 학습
목표는 Discriminator가 "진짜"로 판단할 수 있는 가짜 데이터를 생성하는 것
Discriminator가 Generator가 생성한 데이터를 구분하지 못하게 되면 Generator가 성공적으로 학습된 것
Discriminator와 Generator는 서로 번갈아가며 학습을 진행.
Discriminator는 진짜와 가짜 데이터를 분류하는 성능을 계속 높이고, Generator는 Discriminator를 속이기 위해 더 정교한 데이터를 생성하도록 개선
이 과정이 반복되면서 두 모델의 성능이 점점 더 향상

atdawn

복습 복습 복습

이전 포스트

[8week] 시각 지능 딥러닝 (2) : Data Augmentaion, Transfer Learning,

다음 포스트

[10week] 언어 지능 딥러닝

AIVLE

TF-IDF : TermFrequency - Inverse Document Frequency

단어표현

One-Hot-Encoding : 기본

딥러닝 기반의 유사도 판단

자카드 유사도

코사인 유사도

유클리디언 유사도

멘헤튼 유사도

비지도 학습

Clustering

데이터 타입

데이터 표현

Data matrix (object-by-feature structure)

Distance/dissimilarity maxtrix (object-by-object structure)

거리 측정 방법

민코프스키 거리 (Minkowski Distance)

코사인 측정 (Cosine Measure)

클러스터링 접근법

K-menas-clustering

KNN (k Nearest Neighbor)

Ensemble

Word Embedding

Word2Vec : word to vector

+) skipgram : word2Vec data generation (Word2Vec 데이터를 만드는 과정)

정보검색, 추천 시스템

정보 검색

RSS 실습 : 깃허브 복습!

추천 시스템

협업 필터링 CF : Collaborative Filtering

컨텐츠 기반 필터 : Contents-based Filtering

영화 리뷰기반 분석 실습 : 깃허브 복습!

언어 지능 인공 신경망

Linear Function

Linear Regression

Cost Function (Loss Function)

pytorch 실습

Binary Classification

Cost Function (Loss Function)

pytorch 실습

Softmax

Cost Function : Cross Entropy

Nonlinear Functions

신경망 NN : Neural Network

XOR 문제 해결

ANN : ReLU(Rectified Linear Unit)

GAN : Generative Adversarial Networks

[8week] 시각 지능 딥러닝 (2) : Data Augmentaion, Transfer Learning,

[14week] SQL

0개의 댓글