타깃 인코딩
타깃 변수의 정확한 형태는 풀려는 NLP 문제에 따라 다르다.
많은 NLP 작업은 범주형 레이블을 사용한다. 모델은 고정된 한 세트의 레이블 중 하나를 예측해야 한다. 이때 레이블마다 고유한 인덱스를 부여하는 방법이 가장 흔하게 사용된다. 하지만 출력 레이블 수가 너무 커지면 문제가 발생한다. (예- 언어 모델링)
일부 NLP 문제는 주어진 텍스트에서 수치를 예측한다. (예- 수필에 등급 매기기, 음식점 리뷰 평점 예측 등) 이때는 타깃을 범주형 구간으로 바꾸고 순서가 있는 분류 문제로 다룰 수 있다.
계산 그래프
모델은 입력을 변환해 예측을 얻는다. 손실 함수는 모델의 파라미터를 조정하는 피드백 신호를 제공한다. 계산 그래프 데이터 구조를 사용하면 이런 데이터 흐름을 간편하게 구현할 수 있다.
기술적으로 본다면 계산 그래프는 수학식을 추상적으로 모델링한 것이다. 딥러닝에서는 씨아노, 텐서플로, 파이토치와 같은 계산 그래프의 구현이 부가적으로 자동 미분을 구현한다. 자동 미분은 지도 학습 시스템에서 훈련하는 동안 파라미터의 그레이디언트를 얻는 데 필요하다.
추론은 단순히 식에 대한 평가다.
y=wx+b라는 식이 있다고 가정한다. 이 식은 z=wx와 y=z+b로 나눌 수 있다. 그다음 유향 비순환 그래프(DAG)를 사용해 원래 식을 표현할 수 있다.
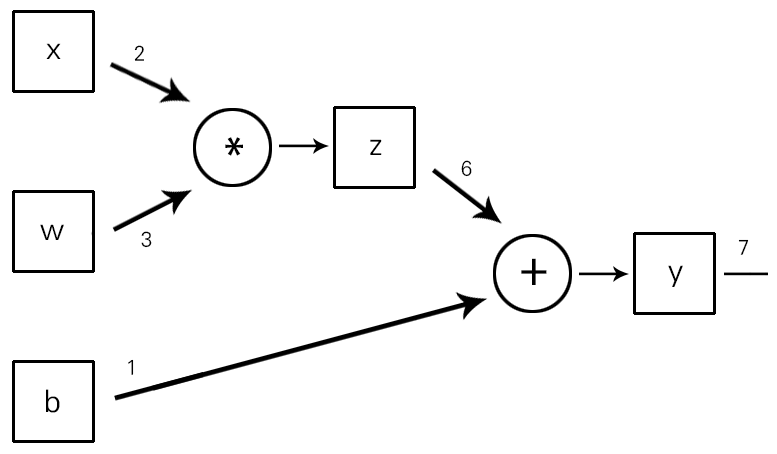
이 그래프의 노드는 곱셈이나 덧셈 같은 수학 연산을 나타낸다. 연산의 입력은 노드로 들어가는 에지이고, 연산의 출력은 노드에서 나가는 에지다.
파이토치를 사용하면 계산 그래프를 쉽게 만들 수 있다!! 다음 포스팅에서 계속!!
