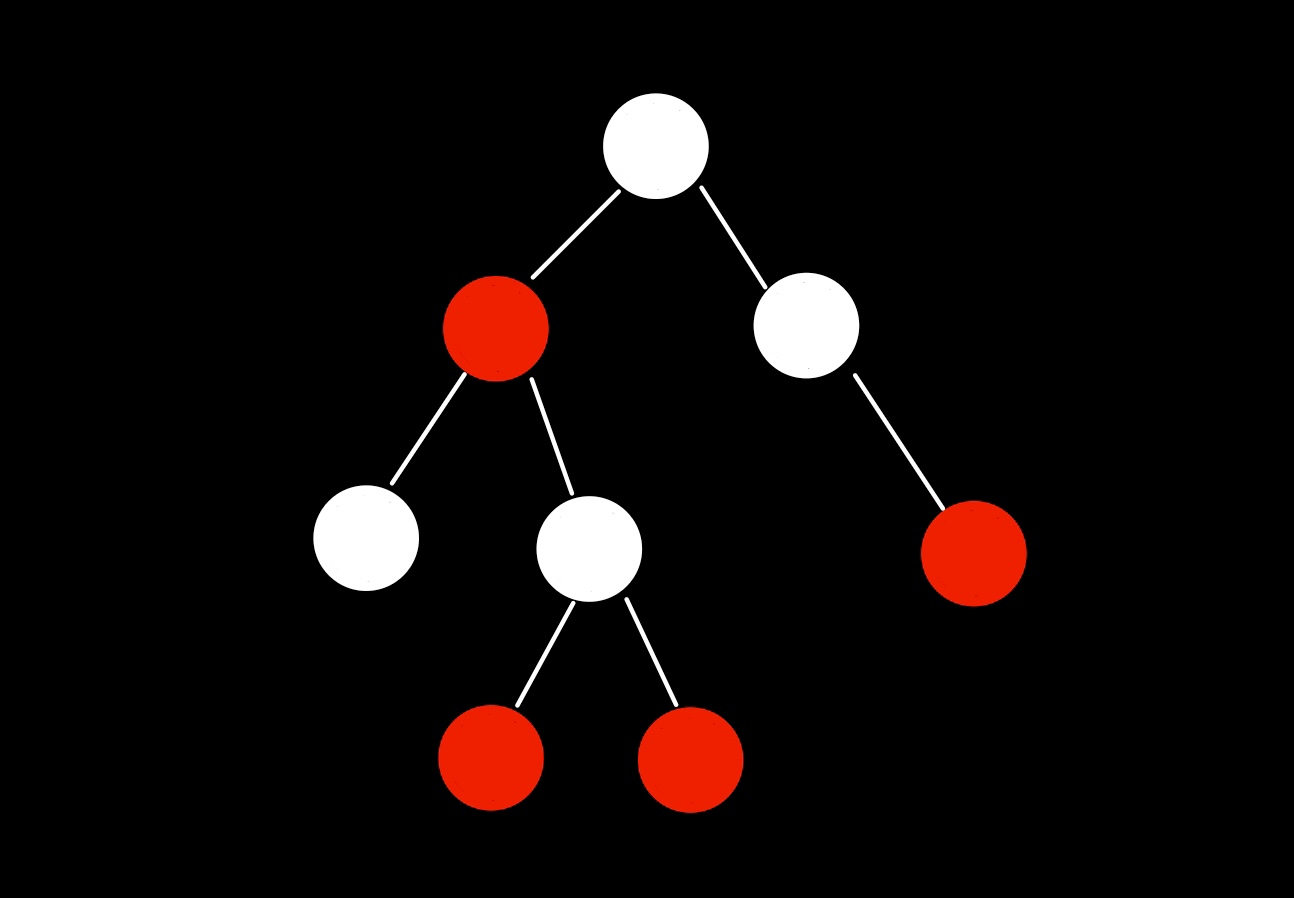
레드블렉 트리는 균형이진트리의 한 종류다.
AVL트리와 많이 비교된다.

레드블랙 트리 규칙

전제

1. 각 노드는 레드 또는 블랙이다.
2. 루트 노드는 블랙이다.
3. 모든 nil 노드는 블랙이다.
4. 레드 노드의 자식 노드는 블랙이다. (레드는 연속될 수 없다.)
5. 어떤 노드든 모든 nil노드까지의 블랙 노드 수는 동일하다. (black height)

+ 삽입되는 노드의 색은 항상 레드로 한다.

Search

specific value search

tree_search(x, k)
	if x == NIL or key[x] == k				// if target x is NIL or key of x is the searching key
    	return x							// return target
    if k < key[x]							// if searching key is less then target key
    	return tree_search(left[x], k)		// search in left subtree
    else									// if searching key is greater than target key
    	return tree_search(right[x], k)		// search in right subtree
    	

minimum search

이진트리의 성질을 갖고 있으므로 계속 왼쪽으로 따라 들어가면 된다.

tree_min()
	while left[x] != NIL	// check if left child of the target x is NIL
    	do x = left[x]		// if not NIL, make left child the next target
    return x				// when target x's left child  is NILL

maximum search

마찬가지로 오른쪽으로 따라 들어가면 된다.

tree_max()
	while right[x] != NIL	// check if left child of the target x is NIL
    	do x = right[x]		// if not NIL, make left child the next target
    return x				// when target x's left child  is NILL

Successor

석세서 개념은 삭제 개념에서 나오게 되는데,
다음 그 자리를 어떤 노드가 계승하는가에 대한 것이다.
해당 노드의 값보다 큰 노드들 중 가작 작은 값의 노드가 석세서이다.

tree_successor(x)
	if right[x] != NIL					// if right subtree exists
		return tree_min(right[x])
    y = p[x]							// if right subtree does not exist, set y the parent of x to find successor among ancestors
    while y != NIL and x == right[y]	// find until root node and  while x is being right child
    	do x = y						// make parent new target x
        y = p[y]						// make grandparent new parent of new x
   	return y

predecessor

석세서와 반대, right <-> left

Rotation

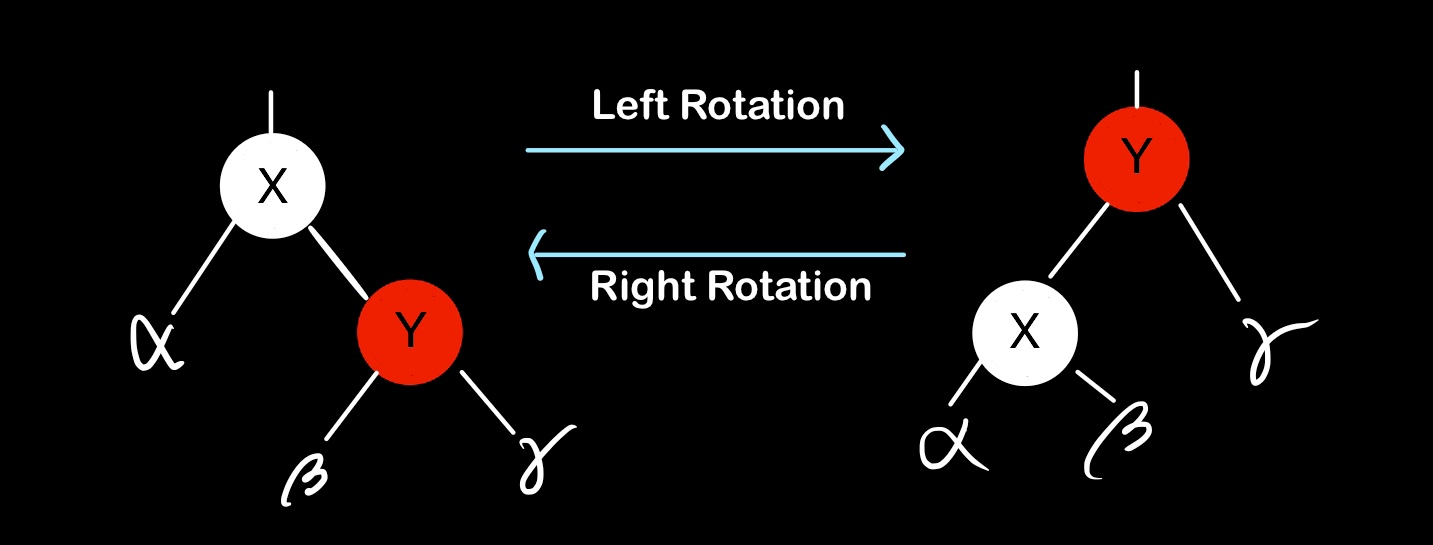
Left rotation

only when y == right[x] && y != NIL

left_rotate(RBT, x):
	y = right[x]				// set y
    right[x] = left[y]			// turn y's left subtree into x's right
    p[left[y]] = x				// link y's left child's parent to x
    p[y] = p[x]					// link x's parent to y
    if p[x] == nil[RBT]			// if x is the root node
    	then root[RBT] = y		// make y the new root node
    else if x == left[p[x]]		// if x has a parent, and x is left node of the parent
    	then left[p[x]] = y		// make y new left node of x's ex-parent
    else
    	right[p[x]] = y			// make y right node of x's ex-parent
	left[y] = x					// now make x left node of y
	p[x] = y					// and y becomes parent of x

Right rotation

left rotation을 반대로 해주면 right rotation

right_rotate(RBT, x):
	y = left[x]
    left[x] = right[y]
    p[right[y]] = x				
    p[x] = p[y]					
    if p[x] == nil[RBT]			
    	then root[RBT] = y
    else if x == right[p[x]]		
    	then right[p[x]] = y		
    else
    	left[p[x]] = y			
	right[y] = x					
	p[x] = y		

Insert

insert(RBT, z)
	y = nil[RBT]				// y is the follower of x
    x = root[RBT]				// set target x = root
    while x != nil[RBT]			// until target reaches nil node
    	do y = x				// put y in target x's place, so y steps down to x's place
        if key[z] < key[x]		// if key of z is less than x's
        	then x = left[x]	// x steps down to the left
        else					// if key of z is greater than x's
        	x = right[x]		// x steps down to the right
    p[z] = y					// when x reaches nil node, y becomes the parent of z
    if y == nil[RBT]			// if there is no node in the tree
    	then root[RBT] = z		// z become the root node
    else if key[z] < key[y]		// if key of z is less than parent node y
    	then left[y] = z		// z becomes left child of y
    else						// if kye of z is greater than parent node y
    	right[y] = z			// z becomes right child of y
    left[z] = nil[RBT]			// since z is the vaild end node, it should have nill node of left
    right[z] = nil[T]			// add right nil node
    color[z] = RED				// <ONLY RB TREE> new node is red
	RB_insert_fixup(RBT, z)		// <ONLY RB TREE> make the tree stick to the rule

이때 레드 노드가 삽입된 것이므로
1. 각 노드는 레드 또는 블랙이다 => 만족
2. 루트 노드는 블랙이다 => 레드면 블랙으로 바꾸면 됨
3. 모든 nil 노드는 블랙이다 => 만족
4. 레드 노드의 자식 노드는 블랙이다 => 연속된 레드가 올 가능성
5. 어떤 노드든 모든 nil노드까지의 블랙 노드 수는 동일하다 => 레드이므로 만족

따라서 RB_insert_fixup에서는 2번 조건일때는 단순히 black으로 바꿔주면 되므로 주로 4번 조건에 대한 경우만 신경써주면 된다.

4번 조건에 대한 불만족 경우의 수는 6가지다. 그런데 case 1,2,3과 case 4,5,6은 left-right 경우로 대칭적이다. 따라서 case 4,5,6에는 case 1,2,3의 로직을 그대로 활용하면 된다.

CASE 1

z의 uncle이 red일 때

(a) z가 left child일 경우

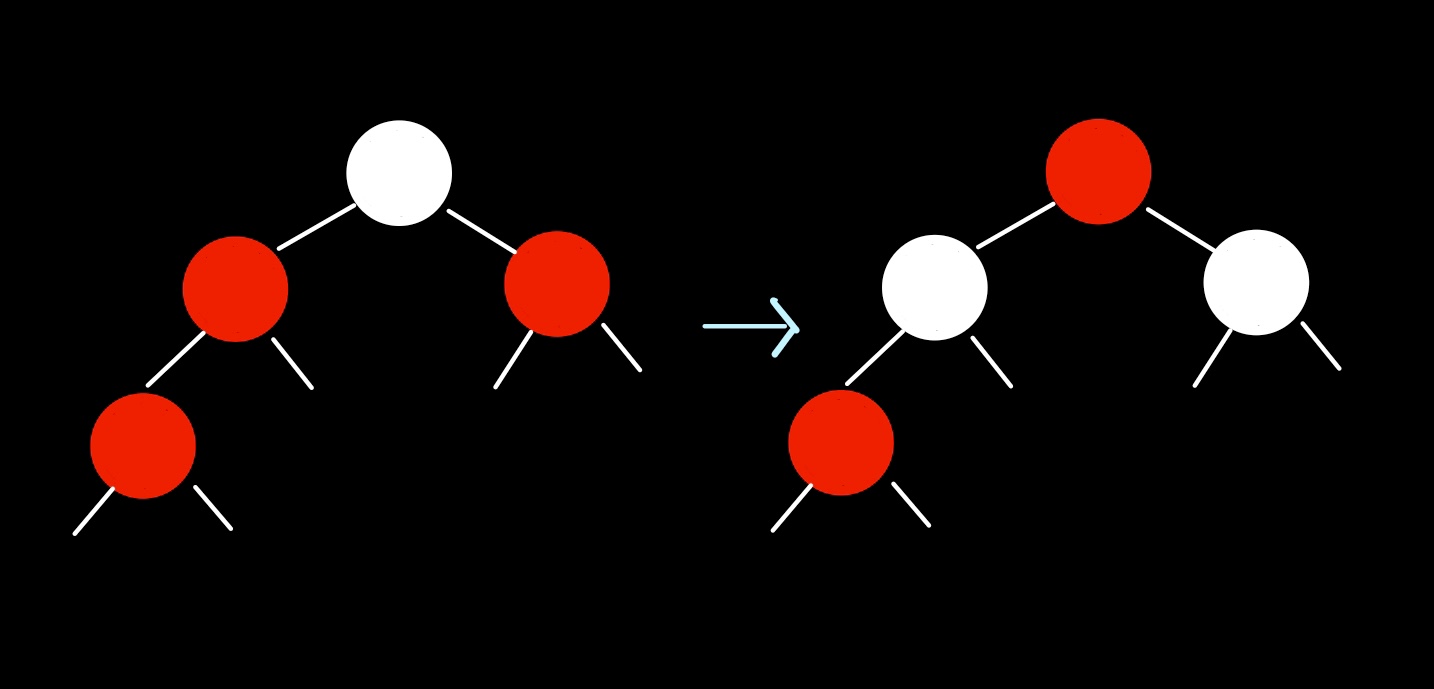
(b) z가 right child일 경우

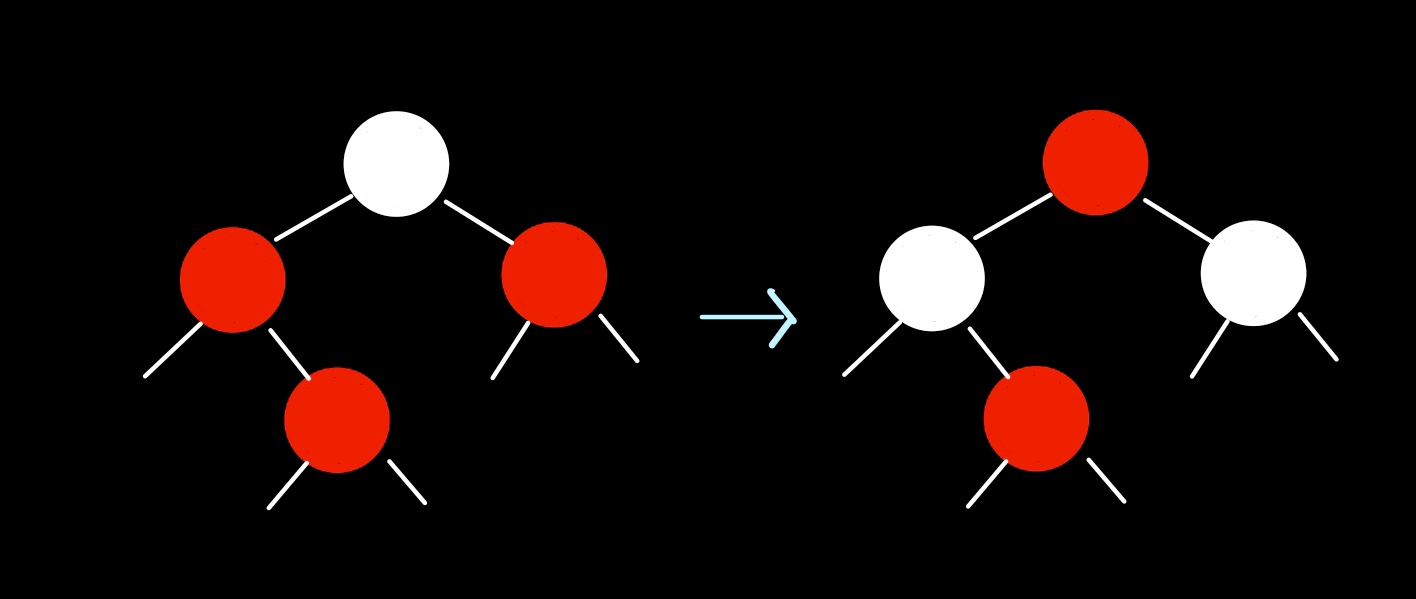
할아버지 노드의 색(black->red)과 부모 노드 및 uncle의 색(red -> black)을 바꿔준다.
4번 규칙 위반이 할아버지 노드로 이전될 수 있지만, 반복해서 루트 노드까지 위반 내용을 해결해주면 된다.

CASE 2,3

z의 uncle이 black(nil 포함)일 때
(a) z가 right child => CASE 2
(b) z가 left child => CASE 3

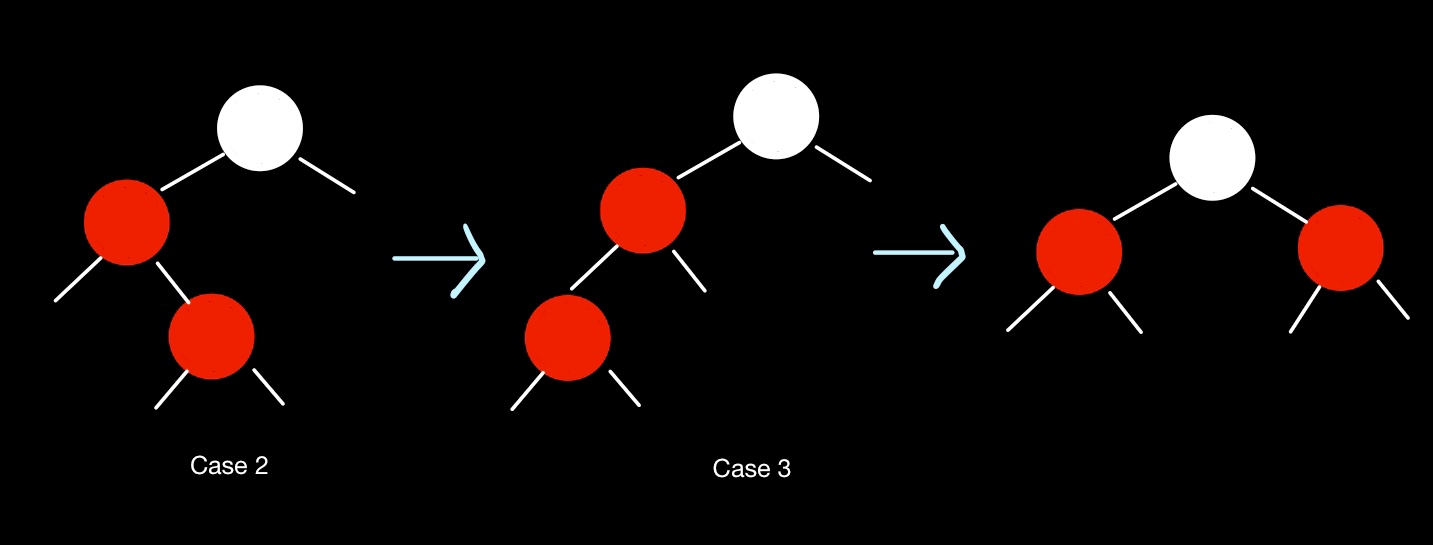
CASE 3인 상태로 만들어서 할아버지 노드 중심 right rotation + 할아버지 색과 right rotation 끝 노드의 색을 바꾸는 것으로 해결
CASE 2는 left rotation을 통해 CASE 3로 만들어서 같은 방법으로 해결

RB_insert_fixup(RBT, z)
	while p[z] != NIL && color[p[z]] == RED			// while RED is successive
    	if p[z] == left[p[p[z]]]					// CASE 1,2,3
        	y = right[p[p[z]]]						// y is uncle node of z
            if color[y] == RED						// CASE1 : if the unclude is RED
                color[p[z]] = BLACK					// parent of z becomes BLACK
                color[y] = BLACK					// uncle node y becomes BLACK
                color[p[p[z]] = RED					// grandparent of z becomes RED
                z = p[p[z]]							// grandparent becomes new z to solve problem
            else									// CASE2, CASE3: if the uncle is BLACK
            	if z == right[p[z]]					// CASE2 : if z is the right child
                	z = p[z]						// z steps up
                    left_rotate(RBT, z)				// left rotation 
                color[p[z]] = BLACK					// CASE3 : if z is the left child
                color[p[p[z]]] = RED				// grandparent becomes RED
                right_rotate(RBT, p[p[z]])			// right rotation
		else
        	/* ---------------------------------- */
        	/* == the same logic as CASE 1,2,3 == */
            /* symmtric as to z is on th right    */
            /* ---------------------------------- */
 	color[root[RBT]] = BLACK						// make root node BLACK

Delete

자식 노드가 없는 경우 => 그냥 삭제
자식 노드가 한개인 경우 => 자식 노드를 부모 위치로 옮겨옴
자식 노드가 두개인 경우 => successor가 해당 자리를 계승

delete(RBT, z)										// z will be deleted
	if left[z] == nil[T] or right[z] == nillT]		// if z has only one child
		then y = z									// z will be deleted
	else											// z has two childs
		y = tree_successor(z)						// successor of z node will be deleted
	if left[y] != nil[RBT]							// if y has a child
		then x = left[y]							// set y's left child as x
	else											// if y has no child
		x = right[y]								// set y's right child as x
	p[x] = p[y]										// make x's parent y(deleted)'s parent
	if p[y] == nil[RBT]								// if y is root node
		then root[RBT] = x							// x becomes new root node
	else if y == left[p[y]]							// if y is left child
		then left[p[y]] = x							// x becomes the left child of the parent of deleted y
	else											// if y is right child
		right[p[y]] = x								// x becomes the right child of the parent of deleted y
	if y != z										// if z's successor is deleted
		then key[z] = key[y]						// copy y(successor)'s data into z (z's ex-data is deleted)
	if color[y] == BLACK							// if deleted node is BLACK (deletion of RED node is no problem)
		then RB_delete_fixup(RBT, x)				// fixup the rule
	return y

삭제 시 삭제된 노드의 색이 RED일 경우는 문제가 안 됨 -> black height는 그대로
그러나 삭제된 노드가 BLACK일 경우 문제가 됨 -> RB_delete_fixup(RBT, x)

1. 각 노드는 레드 또는 블랙이다 => 만족
2. 루트 노드는 블랙이다 => 레드면 블랙으로 바꾸면 됨
3. 모든 nil 노드는 블랙이다 => 만족
4. 레드 노드의 자식 노드는 블랙이다 => 삭제된 노드의 자식노드를 레드에서 블랙으로 변경
5. 어떤 노드든 모든 nil노드까지의 블랙 노드 수는 동일하다 => extra black 개념으로 해결

extra black을 가진 노드가 black -> doubly black 노드
extra black을 가진 노드가 red -> red & black 노드

이 상태를 해결하는 기본적인 아이디어는
extra black을 부모 노드로 계속 이전하는 것임
-> red & black 상태가 되면 black 노드로 만듦
-> 루트 노드가 doubly black 상태가 되면 extra black을 제거
(이 때 현재 상태를 보는 노드의 형제 노드는 NIL 노드가 아니라는 조건이 있어야 한다.)

총 8가지 CASE가 있지만, Case 1,2,3,4와 5,6,7,8은 left-right 대칭이다.

Case 1

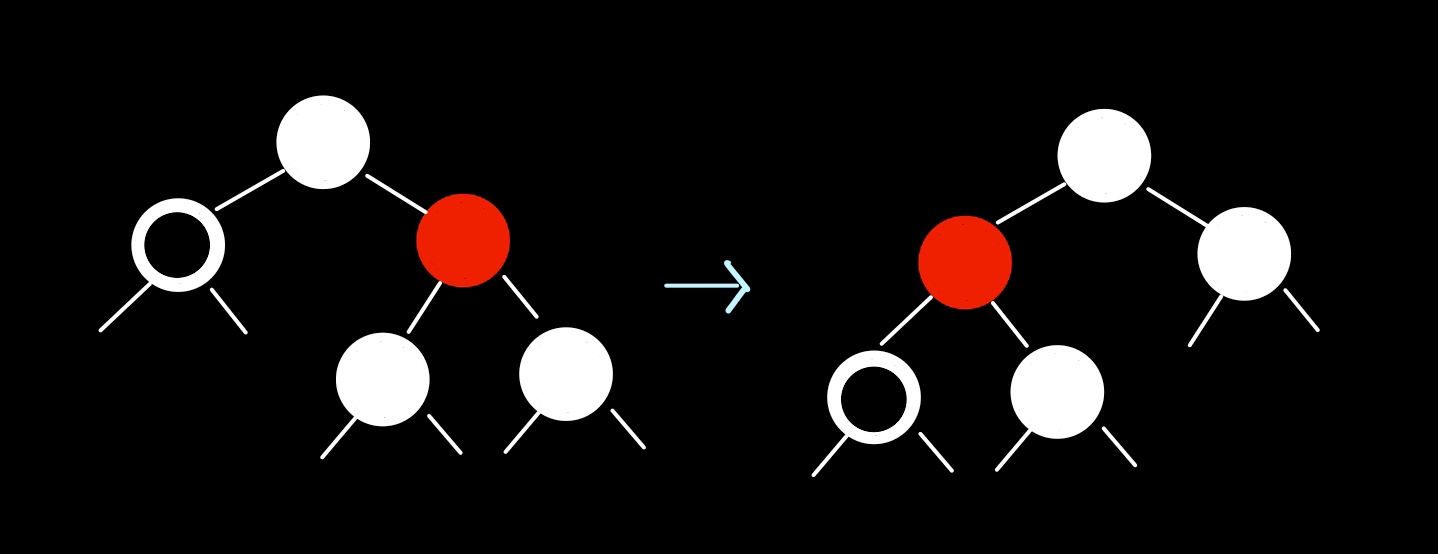
uncle노드가 레드일 때를 Case 1이라고 하고, left rotation + 색 변경을 통해 uncle 노드를 블랙인 경우로 만든다. 이후 extra black을 이전시키면 된다. (Case 2,3,4)

Case 2

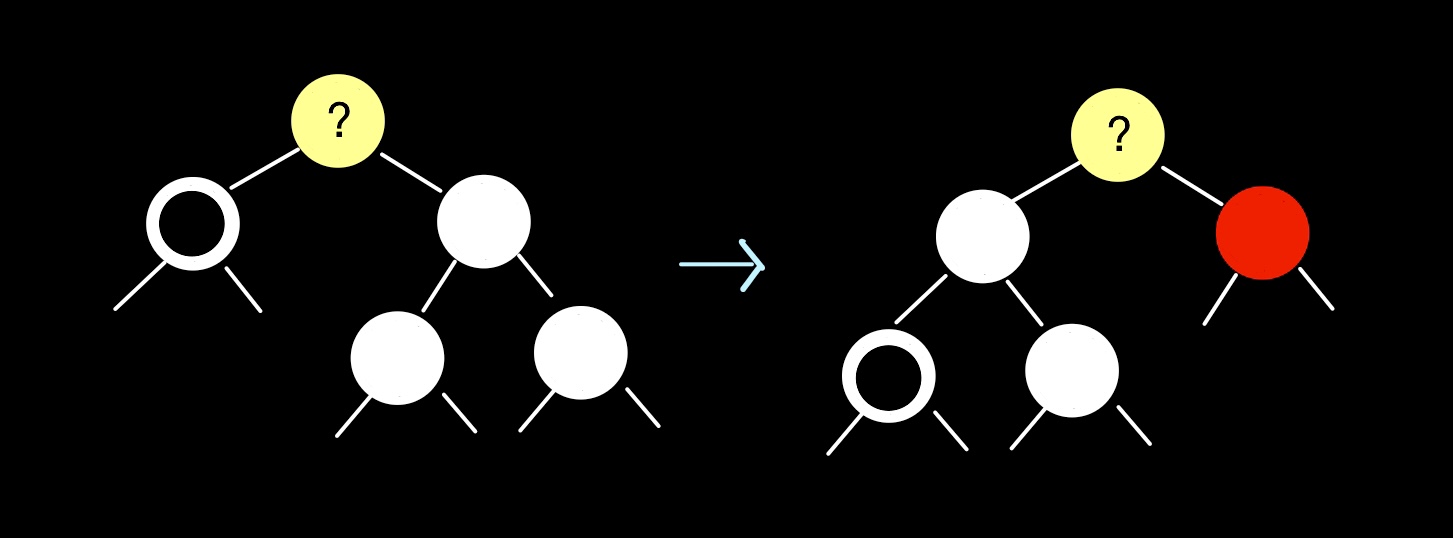
doubly black과 그냥 블랙에서 블랙을 하나씩 차감하고 레드 또는 블랙인 부모는 블랙을 하나 더해준다. 그러면 부모 노드는 doubly black 또는 red & black 이 된다.

Case 3

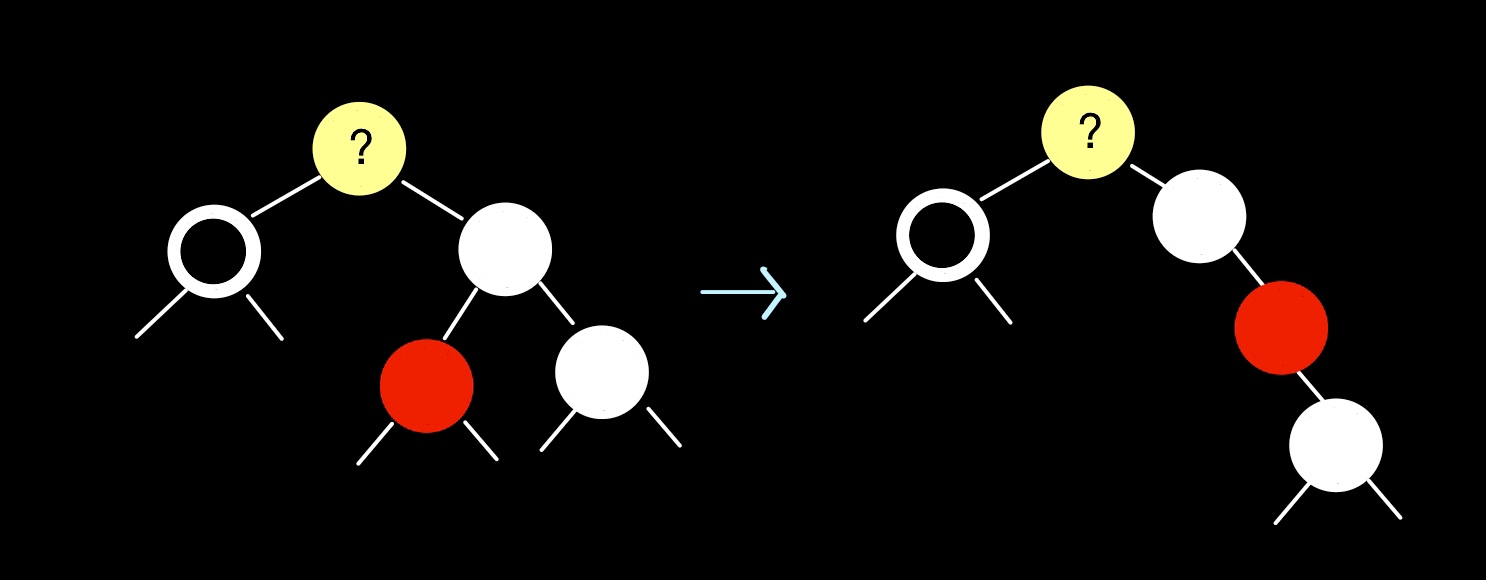
Case 4로 만들어 준다. uncle 노드를 레드로, uncle의 왼쪽 자식을 블랙으로 바꾼 뒤 right rotation을 진행한다.

Case 4

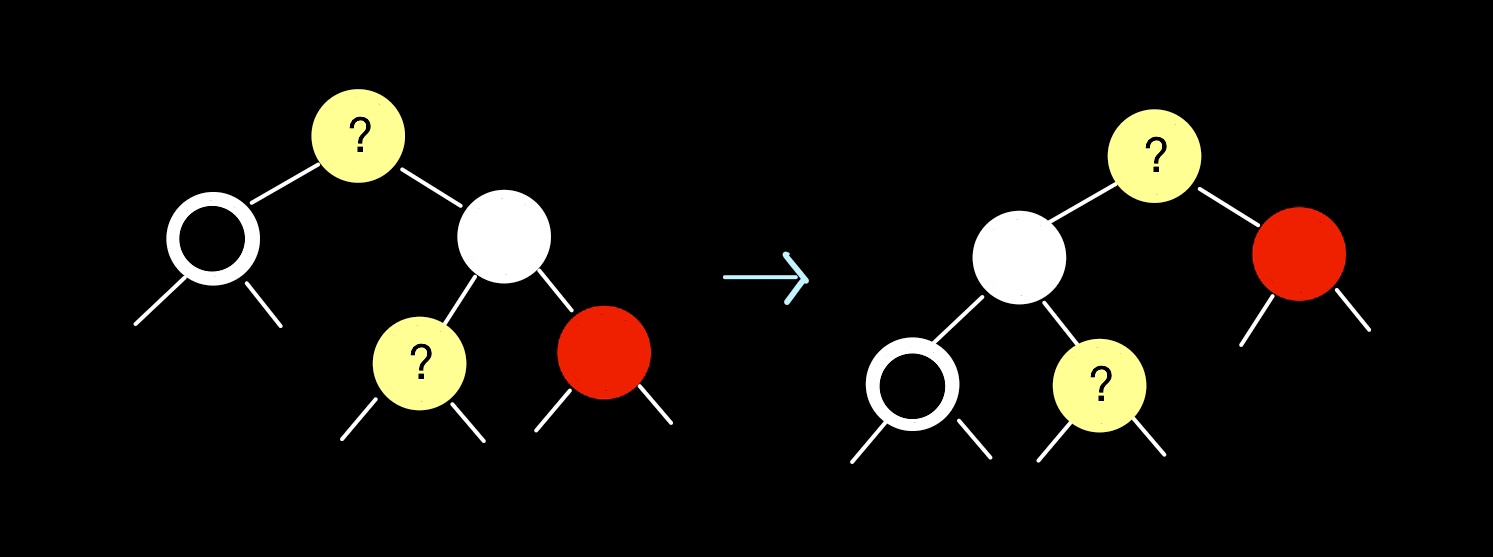
uncle 노드와 부모 노드의 색을 서로 바꿔준 뒤 left rotation을 진행한다.

모든 과정이 끝나면 black height를 맞춰주기 위해 doubly black의 extra black을 부모노드로 계속해서 이전한다.

RB_delete_fixup(RBT, x)
	while x != root[T] and color[x] == BLACK
		if r == left[p[x]]
			w = right[p[x]]
			if color[w]= RED
				color[w] + BLACK										// CASE 1
				color[p[x]] < RED
				left_rotate(RBT, P[x])
				w = right[p[r]]
			if color[left[w]] == BLACK and color[right[w]] == BLACK
				color[w] = RED											// CASE 2
				x = p[x]
			else if color[right[w]] == BLACK
				color[left[w]] = BLACK									// CASE 3
				color[w] = RED
				right_rotate(RBT, w)
				w = right[p[x]]
				color[w] = color[p[x]]									// CASE 4
				color[p[x]] = BLACK
				color[right[w]] = BLACK
				left_rotate(RBT, p[x])
				x = root[RBT]
		else
			/* ---------------------------------- */
			/* == the same logic as CASE 1,2,3,4  */
			/* symmtric as to z is on th right    */
			/* ---------------------------------- */
		color[x] = BLACK

참고로 아래 웹페이지에서 레드블랙 트리를 테스트 해볼 수 있다.
https://www.cs.usfca.edu/~galles/visualization/RedBlack.html