Hybrid Retreival에는 크게 RRF (Reciprocal Rank Fusion) 방식과 CC (Convex Combination) 방식이 있다.
CC 방식에 대해서는 이전의 블로그 글을 참고하자.
이번 글에서는 기존 RRF의 예상되는 문제점과, 그 문제점을 해결하고자 시도한 SRRF에 대해 소개한다. 내용은 모두 pinecone의 논문 An Analysis of Fusion Functions for Hybrid Retrieval의 내용이며, 이 글을 해당 논문의 간단한 정리 및 리뷰 성격으로 봐주시기 바란다.
RRF란?
먼저, RRF가 무엇인지 알 필요가 있다. 메인 아이디어는, semantic 점수와 lexical 점수를 서로 합칠 때에 점수 분포 등이 다르기에, 각 문서의 순위를 활용하여 합치자는 것이다.
서로 다른 retrieval 방법을 이용해 획득한 점수에 따라, 각 문서들은 몇 번째로 높은 점수를 가지고 있는지 순위를 구할 수 있을 것이다. 그렇게 아래 표와 같은 결과를 얻었다 생각해보자.
| 문서 이름 | semantic 순위 | lexical 순위 |
|---|---|---|
| 문서 A | 1 | 5 |
| 문서 B | 4 | 3 |
| 문서 C | 3 | 2 |
어떤 문서가 제일 좋은 문서일까? 여기서 순위만을 활용하자면, 두 semantic과 lexical 순위를 더한 값이 가장 작은 것이 제일 좋은 (쿼리와 관련성이 높은) 문서라고 할 수 있지 않을까?
그렇게 계산을 하면 문서 A는 6, 문서 B는 7, 문서 C는 5로 C가 가장 관련성이 높은 문서라고 결론지을 수 있다.
이러한 원리를 수식화하여 정리한 것이 RRF이다.
여기서 는 semantic retrieval에서의 순위, 는 lexical retrieval에서의 순위가 되겠다. 또한, 는 파라미터 값이다.
파라미터는 RRF를 처음 제안한 논문에서는 60으로 지정하였다.
그러나, 본 논문에서는 파라미터에 여러 값을 지정하고 그 결과를 살펴보며, 해당 값이 hybrid retrieval 성능에 영향을 미친다는 것을 검증하였다. 구체적인 방식과 얼마나 차이가 나는지에 대해서는 원 논문을 살펴보자.
RRF의 문제
RRF는 relevance score 그 자체를 이용하지 않는다. 그렇기 때문에, 점수의 분포에 대한 정보가 손실되는 문제점이 존재한다.
예를 들어보자. 위의 표 예시에서 실제 점수가 아래와 같았다고 해보자.
| 문서 이름 | semantic 순위 | lexical 순위 | semantic 점수 | lexical 점수 |
|---|---|---|---|---|
| 문서 A | 1 | 5 | 0.9 | 0.7 |
| 문서 B | 4 | 3 | 0.1 | 0.71 |
| 문서 C | 3 | 2 | 0.15 | 0.72 |
문서 A의 semantic 점수가 다른 문서에 비해 매우 높지만, 단순 순위를 계산하자 그 정보가 사라진 것을 볼 수 있는가? 만약 점수를 기반으로 hybrid retrieval 점수를 구했다면 당연히 문서 A가 가장 쿼리와 관련성이 높은 문서로 선정되었을 것이다. 하지만 점수를 순위로 바꾸면서, 각 retrieval의 점수 분포와 관련된 정보를 알 수 없어졌다. 그래서 RRF로 계산하면 문서 C가 가장 관련성이 높은 문서로 채택될 것이다.
얼마나 영향을 미칠까?
여기서 알고 싶은 것은 이러한 정보 손실이 실제로 성능에 악영향을 얼마나 끼치는지이다.
그렇다면 일단 정보 손실이 적은 방법이 필요할 것이다.
이제 정보 손실이 적은 RRF 방법을 소개한다.
먼저, sigmoid 함수부터 알아야 한다.
sigmoid 함수
ML을 공부한 분들은 sigmoid 함수가 매우 익숙할 것이다. 기본적인 sigmoid 함수는 아래와 같은 식을 가진다.
이는 아래와 같은 모양의 그래프로 나타나는 것을 알고 있을 것이다.
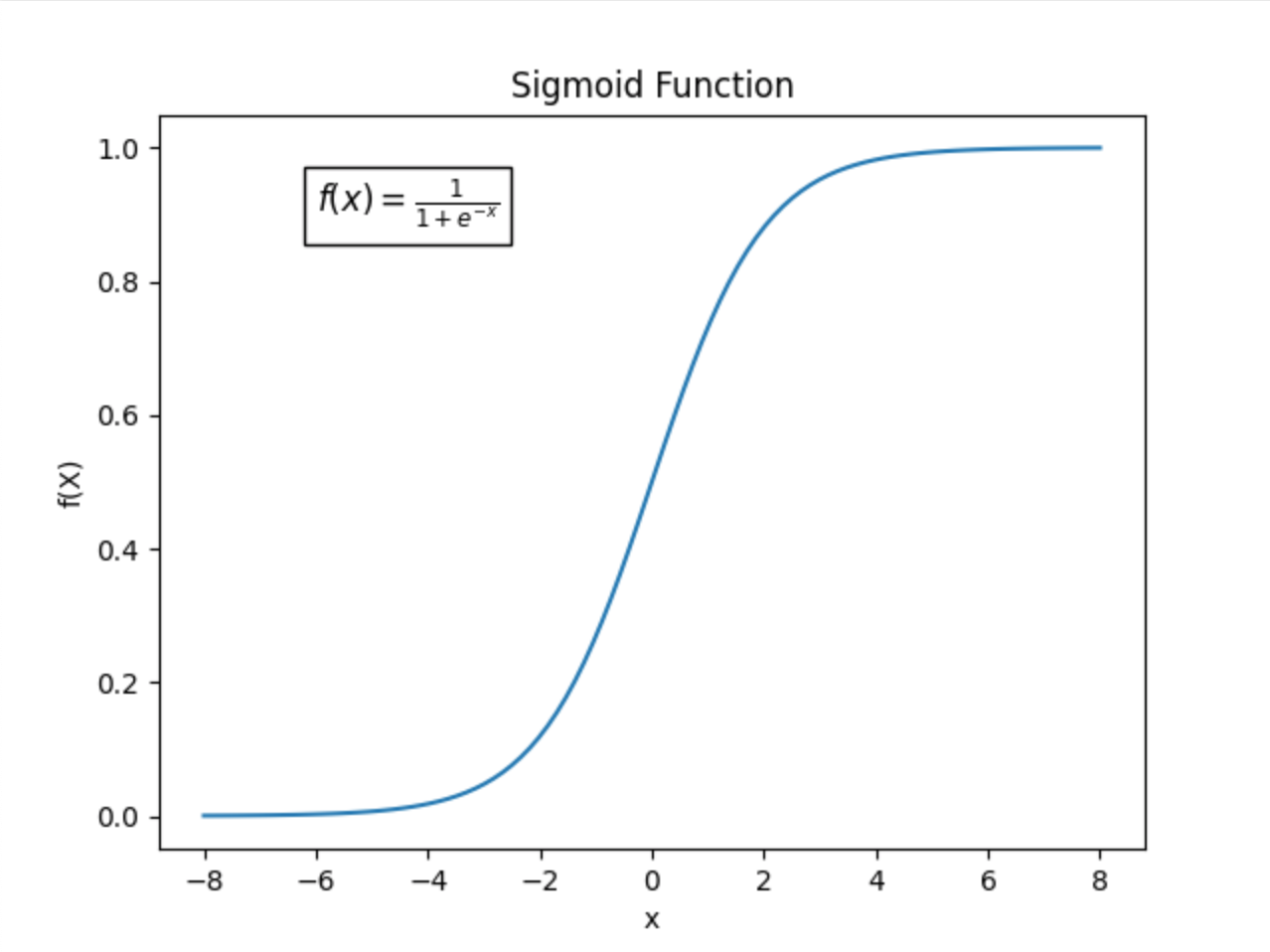
의 값이 작아지면 시그모이드 함수의 결과값은 0으로 급격히 수렴한다. 반면에 의 값이 커지면 시그모이드 함수의 결과값은 1로 급격히 수렴한다.
이러한 특성을 활용해서 ML에서는 binary classification의 activation 함수로 많이 쓰인다.
자, 그렇다면 이런 시그모이드 변형 식을 생각해보자.
의 값에 따라서 시그모이드 함수가 어떻게 바뀔 지 생각해보자.
의 값이 커지면, 의 값에 따라서 훨씬 민감하게 시그모이드 함수의 값이 반응할 것이다.
실제로 그려 확인해보면 다음과 같다.
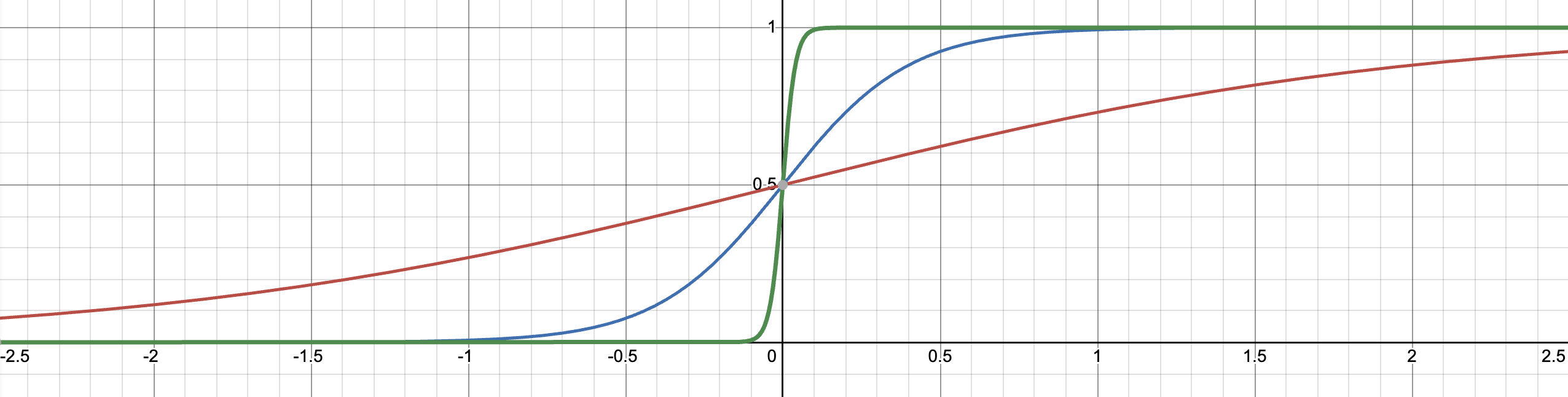
위 차트에서, 빨간색은 가 1, 파란색은 가 5, 초록색은 가 50이다. 가 커질수록 중간의 기울기값이 커지는 것을 볼 수 있다.
sigmoid와 지시 함수
지시 함수라는 용어 등장에 겁먹은 여러분들, 겁먹지 않아도 괜찮다. 생각보다 쉽다.
간단히 말하면, 어떤 조건을 만족하면 1, 아니면 0인 함수이다. 마치 if-else 같은 함수다.
일단, 지시 함수와 sigmoid가 어떻게 관련이 있을까?
가 만약 무한대로 간다고 생각해보자. 그러면 기울기는 점점 가파러져서, 가 0보다 작으면 0, 가 0보다 크면 1인 함수처럼 될 것이다. 즉, 이것을 지시 함수라고 볼 수 있는 것이다!
이렇게 값에 따라 sigmoid 함수를 지시함수와 유사하게 볼 수 있다. 이를 이용해서, 우리는 RRF 함수를 일반화할 수 있다.
sigmoid로 RRF 표현하기
앞서서, 와 같은 문서 d의 랭크를 수학적으로 어떻게 표현할 수 있을까? 그것은 바로 지시함수를 통해서 가능하다.
여기서 은 바로 지시 함수를 의미한다. 또한, 는 쿼리 에 대해서 retrieval이 retrieve한 개의 문서들이다. 그 문서들 각각 ()에 대해서 지시함수를 사용하는 것이다. 어떤 지시함수냐 하면, 만약 랭크를 구하려는 문서 ()보다 의 점수가 높으면 1, 아니면 0을 반환하는 함수이다.
즉, 만약 의 점수보다 높은 점수를 가진 문서가 없다면, 합이 0이 될 것이고, 자연스럽게 그 문서의 랭크는 1, 즉 1등인 문서가 될 것이다.
그렇다면, 지시함수를 sigmoid 함수로 바꿀 수 있다는 것을 기억할 것이다. 지시함수를 sigmoid로 바꾸면 아래와 같이 변한다.
위와 같게 변환할 수 있다.
왜 1이 아니라 0.5를 더해주는 것일까?
그것은 원래 1등의 랭크가 나오는 상황을 생각해보면 쉽다. 만약 가 무한대라면 자기 자신을 제외한 모든 문서들의 값은 0이 될 것이다. 하지만, 자기 자신일 경우, 즉 와 가 같을 경우 값이 0이 되므로 은 0.5이다. 그러면 최종 랭크 값이 1이 되기 때문에 앞에 0.5를 더해주는 것이다.
이제 의문이 들 것이다. 왜 이렇게 바꿔준 것이지?
처음으로 돌아가서 생각해 보자. 이 설명을 시작한 이유는 RRF의 점수의 분포를 반영하지 못하는 성질이 실제 성능에 얼마나 악영향을 미치는가를 알아보기 위함이었다.
이를 위해, RRF에 점수의 분포를 반영할 수 있는 방법을 만들어야 했다. 그리고 위 와 같이 RRF를 바꾸면서 우리는 점수의 분포를 반영할 수 있게 되었다.
값이 무한대에 가까워 질수록, 기존의 RRF와 비슷하게 점수의 분포를 반영하지 못한다. 하지만 값이 낮아질 수록 실제 retrieval 점수들이 반영되어 최종 점수가 계산될 것이다.
이렇게 변형한 RRF를 SRRF라 하며, 아래와 같이 정리할 수 있다.
원 논문에서는 더 엄밀하게 Lipschitz 연속성과 Lipschitz 상수를 통해 설명한다. 더 정확한 설명을 위해서는 원 논문을 참고하자. 전체적인 흐름은 이 블로그와 크게 다르지 않다.
간단하게만 덧붙이자면, Lipschitz 연속인 경우 (시그모이드 함수는 Lipschitz 연속) Lipschitz 상수가 작을수록 함수를 거친 후에 값의 변동이 적다. 즉, 정보가 잘 보존된다.
여기서는 가 곧 Lipschitz 상수이다.
그래서 얼마나 영향을 미치는데?
연구진은 값을 변경하며 SRRF와 기존 RRF와의 성능을 비교해 보았다.
그 결과 값은 아래와 같다.
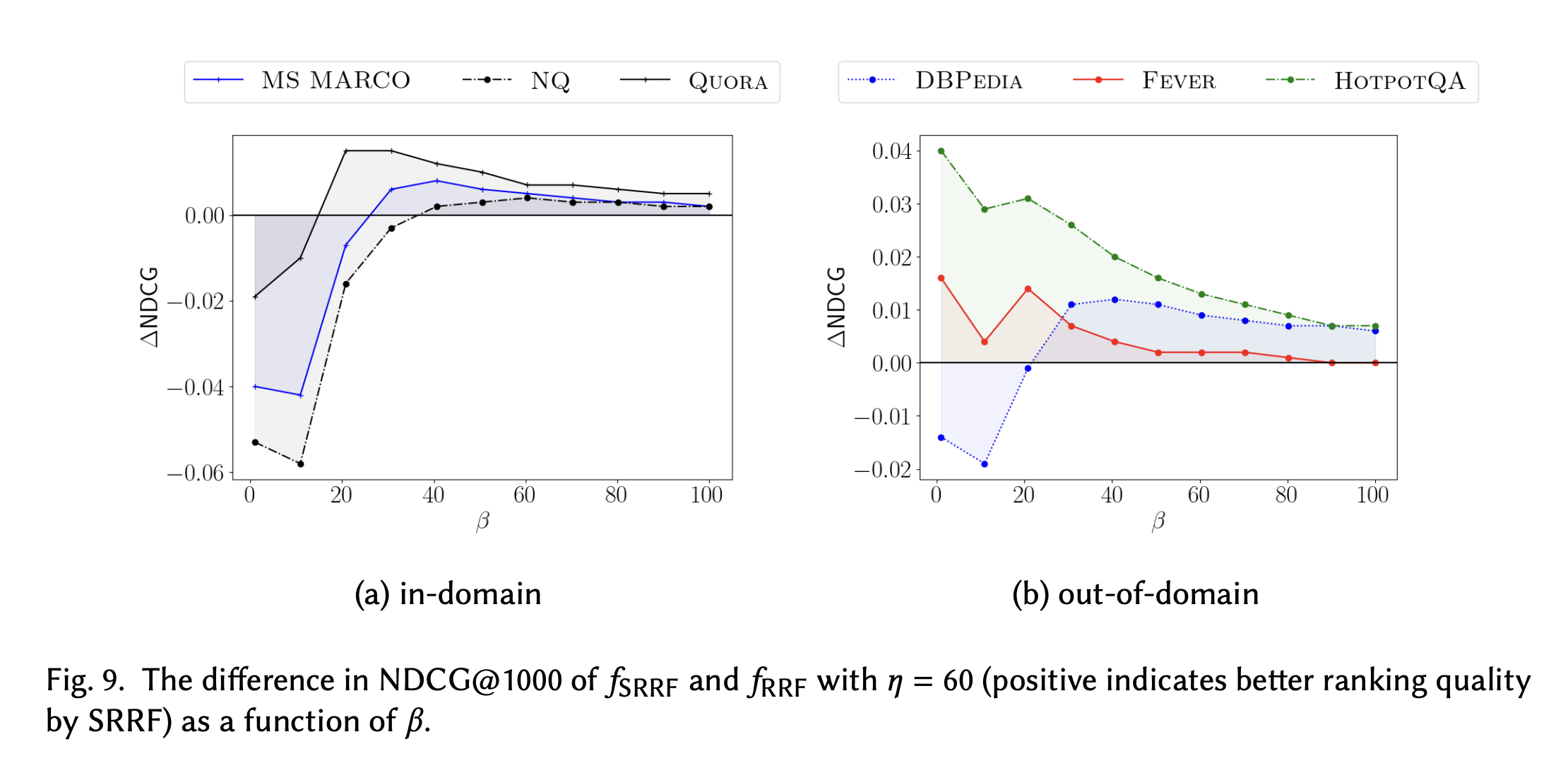
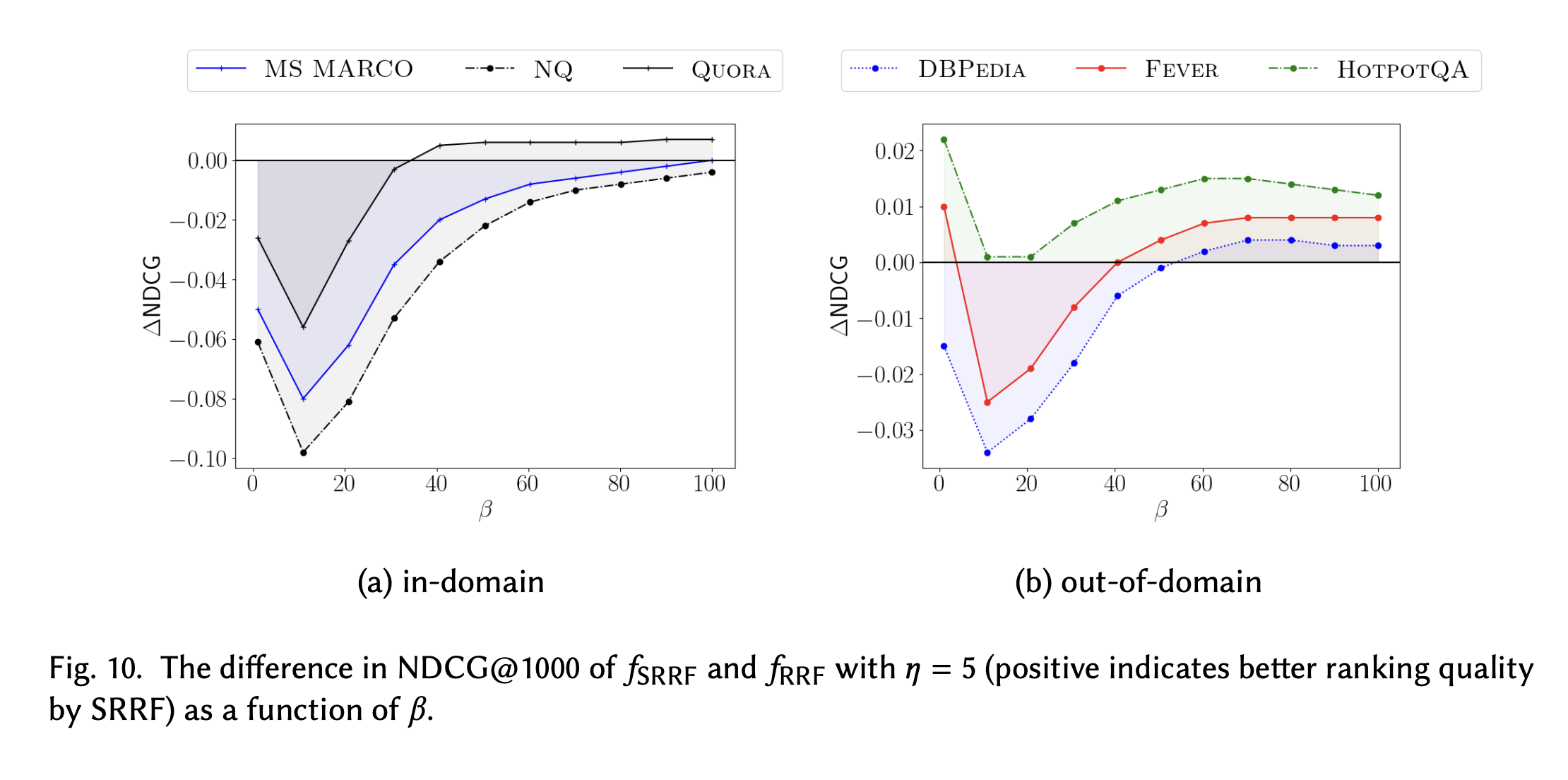
위와 아래 결과의 경우 파라미터 값이 각각 60과 5로 다르다.
전반적으로, 너무 값이 작은 경우 RRF보다 더 낮은 성능을 보인다. 이는, SRRF는 랭크를 가깝게 추산하는 것인데 값이 너무 작으면 이 오차가 커지므로 이러한 낮은 성능을 보이게 된다.
반면, 가 높아질수록 RRF와 유사한 성능을 보이도록 수렴하는 경향을 관찰할 수 있다. 이는 당연하게도 가 무한대에 가까워질수록 RRF와 동일한 수치가 나오며, 그래서 성능이 비슷해지는 것이다.
주목할 만한 것은 적당한 값을 설정했을 때 RRF보다도 성능이 높았다는 것이다. 이러한 결과를 통해서, RRF가 점수의 분포에 대한 정보를 아예 없애는 것이 성능에 어느 정도의 안 좋은 영향을 미쳤음을 알 수 있다. 또한, SRRF를 이용하여 적당한 값을 설정하면 그러한 악영향을 줄일 수 있다는 것도 알게 되었다!
CC vs RRF vs SRRF
마지막으로, 이렇게 개선한 SRRF와 다른 Hybrid retrieval 방법인 CC와의 성능 차이가 궁금할 수 있어, 논문의 실험 결과를 첨부한다.
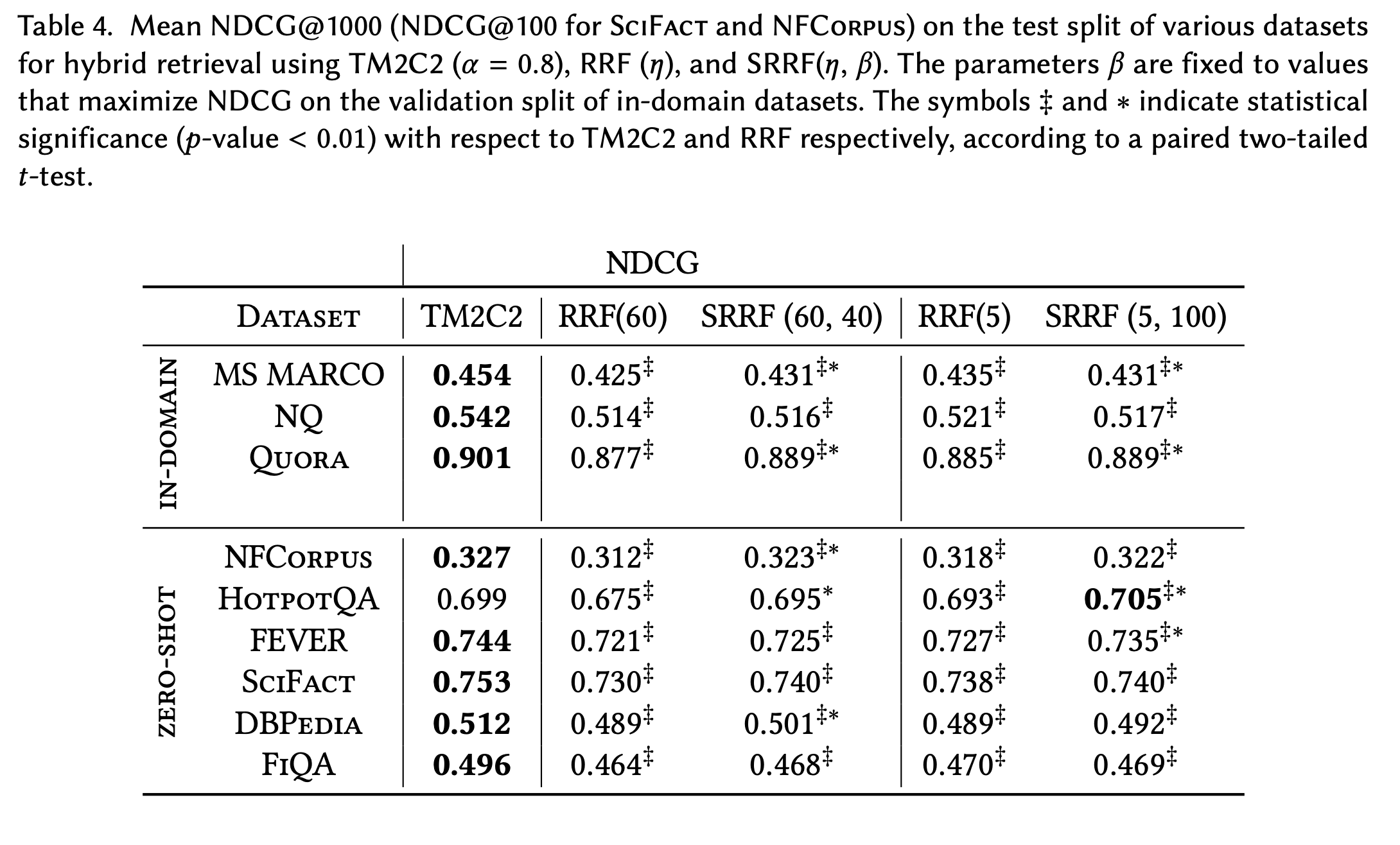
TM2C2는 CC의 tmm normalization 기법을 적용한 것이다. TMM에 대한 설명은 이 블로그 글을 참고하자.
위의 결과 값에서, 대체적으로 RRF보다 SRRF의 성능이 소폭 높음을 관찰할 수 있다.
더불어 주목할 점은, HotpotQA 데이터셋에서 SRRF의 성능이 다섯 개의 retrieval 세팅 중에 가장 높았다는 것이다.
이렇듯, 많은 경우에서는 Hybrid cc (TM2C2)의 성능이 더 우수했지만 SRRF가 더 좋은 대안이 될 수도 있다는 가능성을 볼 수 있다.
AutoRAG에서 사용하기
RAG 자동 최적화 툴인 AutoRAG에서 이런 SRRF를 도입하기 위한 준비를 하고 있다.
해당 깃허브 이슈에서 진행 상황을 확인 가능하다!

