예측 기반 추론 (Prediction Powered Inference, PPI)

오늘 글로 다룰 주제는 예측 기반 추론(Prediction-Powered Inference)입니다

1. 들어가며

RAG의 문제 중 하나는 수요에 비해 메트릭이 적절하지 않다는 것입니다.
자연스러움, 유창함, 사실관계 등 QA 챗봇 RAG 시스템을 구축하는 데에 다양한 평가 기준이 있지만, 이것을 공학적으로 정의하는 것은 매우 복잡합니다. 이를 위해 G-eval, RAGAS 등 LLM을 활용하는 LLM Judge 방법론이 등장하곤 합니다. RAG 시스템의 성능이 좋다고 LLM Judge metric을 측정해 결론을 내려고 했지만, AI의 불완전성이 이 논리를 견고하지 못 하게 만듭니다. 이것은 얼마나 믿을만 한 것일까요?

이러한 일들은 AI 시스템을 이용한 예측을 활용하는 상황에서 빈번하게 나타나는 일들입니다. 수 많은 알고있는 단백질 구조를 통해 만들어진 3차원 구조 prediction들은 단백체학 연구에 사용되고, 우리가 알고 있는 우주의 은하들을 학습하여 다시 우리가 모르고 있는 은하의 사진을 보고 분류하기도 합니다.

이에 대해 오늘 다룰 논문의 저자는 이렇게 말합니다.

Predictions are not perfect, however, which may lead to incorrect conclusions. Moreover, as predictions beget other predictions, these imperfections may cumulatively amplify.

예측은 불완전하기 때문에 잘못된 결론으로 우리를 이끌 수 있고, 이는 누적될 수 있다고 경고합니다.

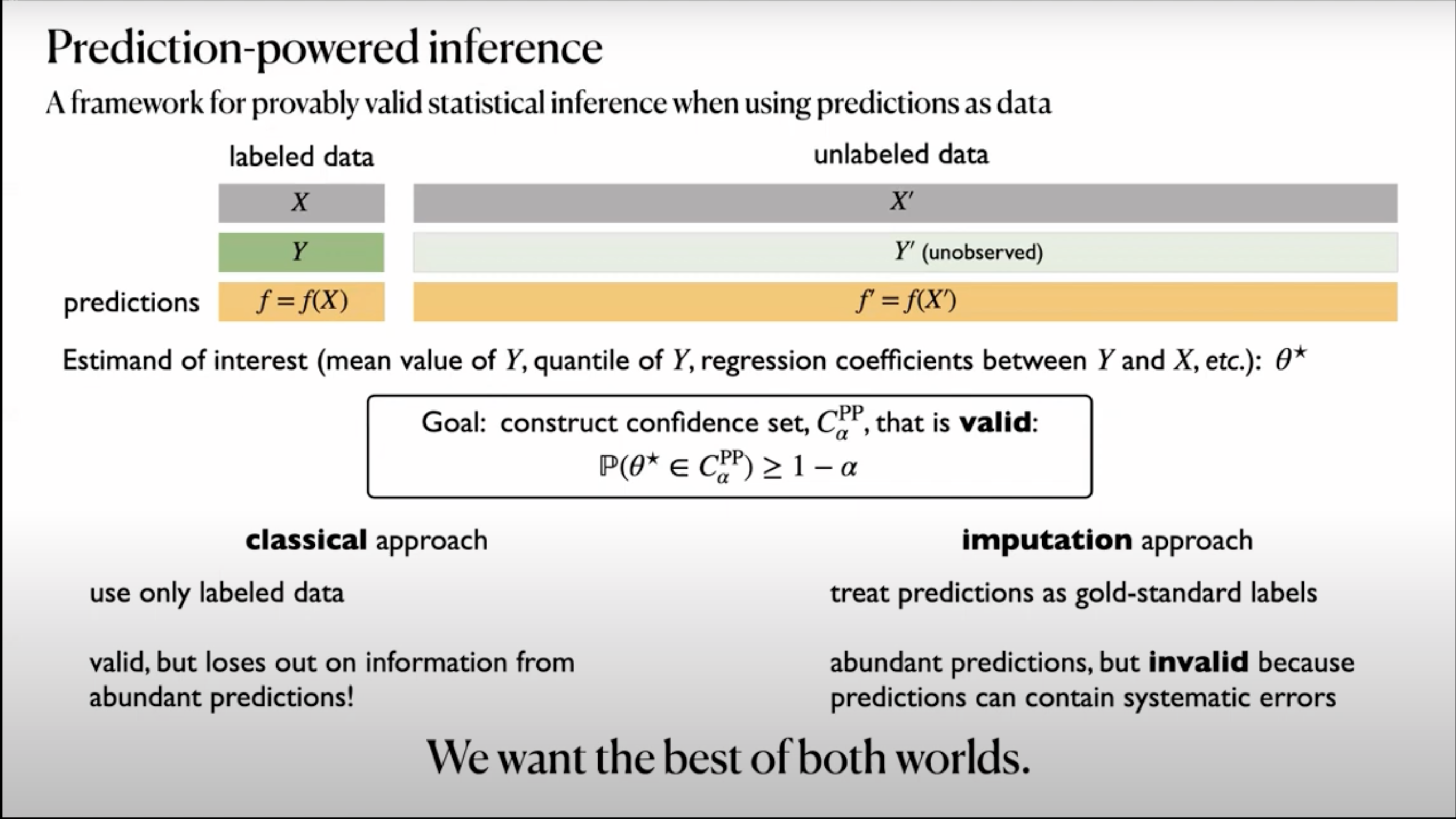
그렇다면 우리는 좀 더 과학적으로 AI를 활용할 수 있을까요?

2. PPI

이 시점에서
우리가 선택할 수 있는 것은 두 가지 입니다

• 풍부한 예측이 주는 정보를 포기하여 신뢰성을 얻고
  이미 labeling되어 있던 데이터만 이용하는 고전적인 방법

• 예측을 gold-standard로 간주하여 풍부한 데이터가 주는 정보를 얻지만,
  AI의 불완전함으로 구조적인 오차를 계속해서 안고 가는 Imputation 접근 방법

그리고, PPI는
라벨링되지 않은 데이터를 활용하면서(풍부한 데이터),
신뢰구간 등 오차를 다룰 수 있는 classic한 방법의 이점을
모두 취하고자 합니다.

3. 원리

문제 상황

n개의 라벨링된 데이터 $(X,Y)$가 있고,
N개의 라벨링되지 않은 데이터 $(X_e)$가 있습니다.
($Y_e$는 라벨링 되지 않아 알 수 없음)

대체로 $N$은 $n$보다 몹시 큽니다.
AI 시스템($f$)은 $X$를 통해 $Y$를 예측합니다

목표는 $Y_e$에 대한 통계치($\theta *$)를 추정하는 것입니다.

솔루션

"gold-standard 데이터셋을 이용해 예측 오차(prediction error)가 imputed estimate에 어떤 영향을 미치는지 정량화한 다음 θ*에 대한 신뢰구간을 구성한다"입니다.

X,Y를 통해 학습된 f를 Xe에 적용하여 얻은 값(f(Xe)≈Ye)을 토대로
f(Xe)의 통계치 θef를 구할 수 있습니다.

AI 시스템 f는 편향된 데이터로 인해 예측 오차를 가지게 됩니다.

θef를 그대로 신뢰하기에는
θ*와는 다를 것이라는 거죠.
(단순 imputed 방법과의 차이)

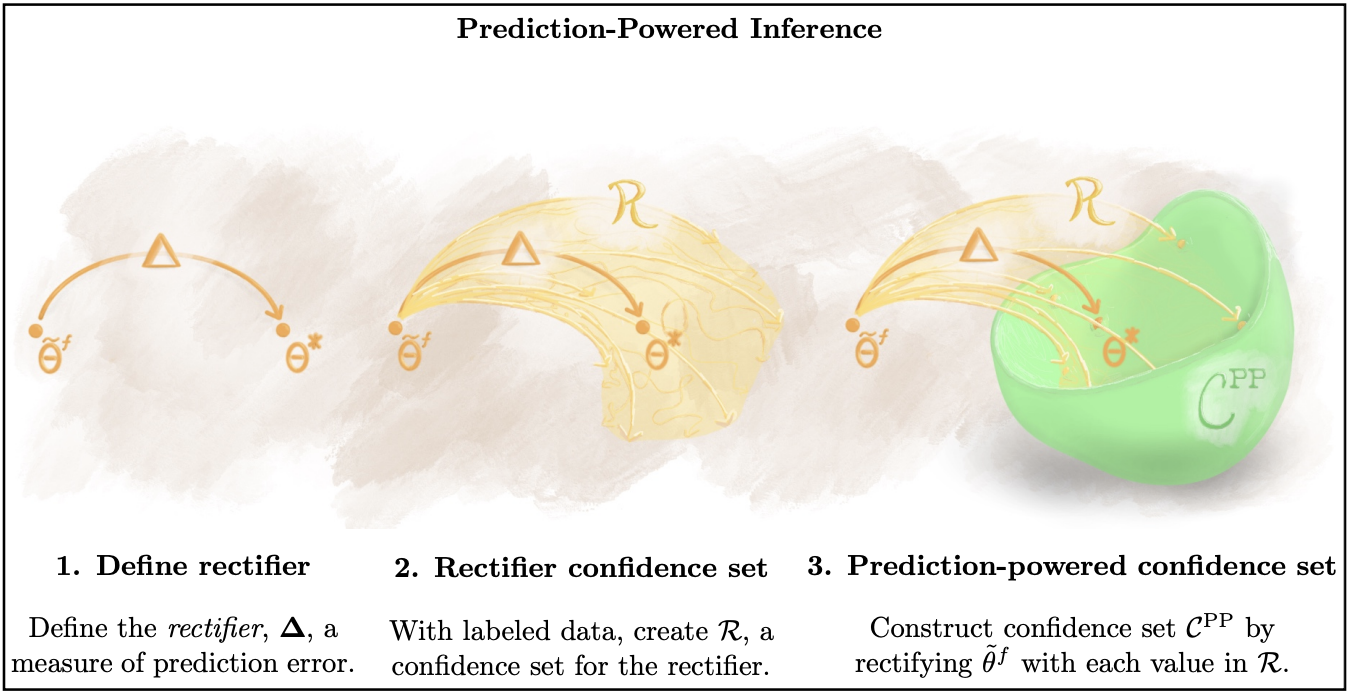
예측 오차로 인해 θ*와 θef 사이에 차이를 메우기 위해 rectifier, ∆를 도입합니다.

그리고 gold standard data(X,Y)를 이용해 ∆의 신뢰구간을 구성합니다.

이를 통해 예측 오차(prediction error)가 imputed estimate에 어떤 영향을 미치는지 정량화할 수 있습니다.

수식

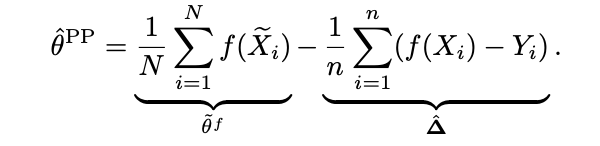
수식적으로는 Xe에 f를 이용해 예측하고
gold standard 데이터인 X,Y를 이용해 f의 예측 오차를 판단한 후
보정(rectify)합니다.

아래는 PPI를 통해 얻어진 신뢰구간과 classic한 방식을 통해 얻어지는 95% 신뢰구간입니다.

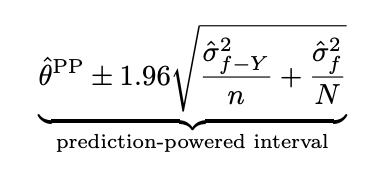
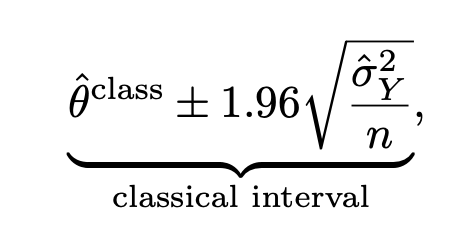
classic한 신뢰구간은
단순히 정답데이터가 많아야(표본의 크기가 커야) 신뢰구간이 좁아지지만,

PPI 방식은 f의 성능이 좋을 수록,
라벨링 되지않은 데이터의 개수가 많을 수록 신뢰구간이 좁아질 수 있기 때문에

현실적으로는 신뢰구간을 좁히는 데에
비교적 제약이 적어집니다.

신뢰 구간을 개념을 도입하면서도
더 많은 양의 데이터를 활용할 수 있다는 것 자체도
장점이라고 할 수 있겠군요

주의점

신뢰구간의 수식을 보면 알 수 있지만,
f의 성능이 떨어질 경우
classical interval보다 신뢰구간이 넓어져버릴 위험이 있습니다.

이는 후속 논문인 PPI++에서 classical 한 방법과 적절히 weight를 주는 방식으로 완화하니 참고해보시길 바랍니다.

더 자세한 내용은 논문과 깃허브를 참고해주세요!

감사합니다.