
72. Edit Distance
풀이
두 스트링일 같게 만드는데 최소한의 연산 횟수를 구하는 문제이다.
추가, 삭제, 교체 이렇게 3가지 연산이 가능하다.
잘 생각해보면 이것도 순차적으로 char을 하나씩 추가해가며 이전 결과를 활용할 수 있다.
1. 이전 결과를 활용하기 위해 word1,word2를 가지고 2d array를 만든다. base case를 위해 역시 각각 스트링앞에 "#"(쓰레기값)으로 패딩을 넣었다.
dp[0][3]이 의미하는 것은 빈 스트링을 "hor"으로 만들려면 몇번의 연산이 필요한지 이다. 3번의 추가가 필요하니 3이 저장된다.
아래처럼 초기값을 세팅해준다.
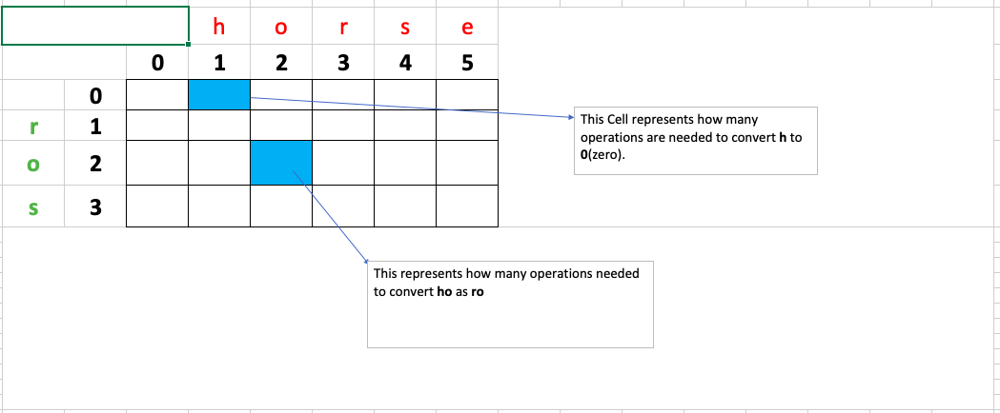
- 순차적으로 테이블을 채워나가는데, 추가,삭제, 교체가 좀 특이하다.
예시를 보면 이해할수있다.Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation:
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
h를 r로 만들어야 한다. 마지막 char이 다르니까 추가든 삭제든 교체는 어떤 작업이 필요하다.
- h 삭제하는 케이스: "h"에서 "h"를 삭제해서 빈스트링으로 만들고, 빈 스트링을 "r"로 만들면 된다.
- 즉,
h 삭제 + 빈 스트링을 r로 만드는 작업횟수 1 = 2
- 즉,
- r을 추가하는 케이스: "h"를 빈 스트링으로 만들고 r을 추가하면 된다.
- 즉,
h를 빈스트링으로 만드는 작업횟수 1 + r 추가 = 2
- 즉,
- h를 r로 교체하는 케이스: 각 케이스에서 마지막 char을 지우고, 둘다 r를 추가한다고 생각한다.
- 즉,
빈 스트링을 빈스트링으로 만드는 작업횟수 0 + r 추가 = 1
- 즉,
위 세가지중에서 가장 적은 연산횟수는 마지막 교체이므로, h->r 연산횟수는 1이 된다.
헷갈릴때에는, 이 전 계산해놓은 값의 결과에서 어떤연산을 추가로해놓으면 되는지 생각해본다.
(ex. h를 빈스트링으로 만드는데 1개연산이 들었네? 그럼 빈스트링이 결과이니까 여기에 r만 추가하면 되는거네.)
ref: https://youtu.be/MiqoA-yF-0M
Time, Space
time O(N^2) space O(N^2)
/**
* @param {string} word1
* @param {string} word2
* @return {number}
*/
var minDistance = function(w1, w2) {
if(w1===w2) return 0;
w1="#"+w1;
w2="#"+w2;
const dp = [...Array(w1.length)].map(row => Array(w2.length).fill(0));
for(let i=0; i<w1.length; i++){
for(let j=0; j<w2.length; j++){
if(i===0){
dp[0][j]=j;
continue;
}
if(j===0){
dp[i][0]=i;
continue;
}
if(w1[i]===w2[j]){
dp[i][j]=dp[i-1][j-1];
}else{
dp[i][j]=Math.min(dp[i][j-1],dp[i-1][j],dp[i-1][j-1])+1;
}
}
}
return dp[w1.length-1][w2.length-1];
};