DAY 9

총 확률의 법칙

A라는 특정 확률 변수에 대해, 모든 가능한 이벤트의 총 확률은 1이다
$P(A) = \sum_n P(A_n) = 1$
예시
스팸메일이다
1. 스팸메일인 경우(0.8) 2. 정상메일인 경우(0.2)
0.8+0.2=1

one step
2개의 변수를 고려 한다면 ( A 와 B ), 두 변수가 연관이 있는 경우, B 가 일어난 상황에서의, A 에 대한 확률 P(A) 는, P(A|B) 의 형태로 표현
예시
예를 들면 스팸메일이다와, 메일 내부에 "스팸"단어가 있다 과 같은 이벤트라면
$P(spam)$ = $P(spam|included)P(included)$ + $P(spam|not~included)P(not~included)$

$P(A) = \sum_n P(A | B_n) P(B_n)$
A 의 모든 확률은, 주어진 Bn에 대해서, 각각의 일어날 확률의 총합

조건부 확률

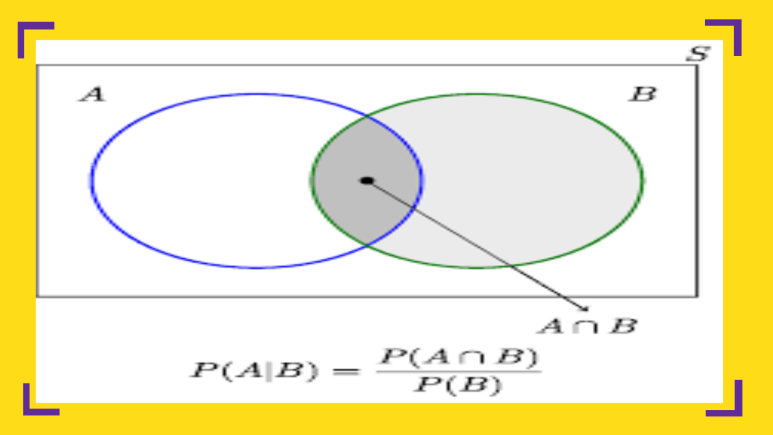
$P(B)$를 양변에 곱하면, $P(A|B)P(B) = P(A \cap B)$ 와 같은 식을 얻을 수 있으며,
이는 곧 $P(A) = \sum_n P(A \cap B_n)$를 의미합니다.
이는, $B$라는 정보가 주어진 상황에서 $A$의 확률은 $B$와 교집합들의 합으로 구성 되어 있다는 것을 이해 할 수 있습니다.

베이지안 이론

참고

$P(A|B) = {{P(A \cap B)} \over {P(B)}}$

$P(B|A) = {{P(B \cap A)} \over {P(A)}}$

$P(A \cap B) = P(B \cap A),$ #상호배반적일 때 가능

$P(A|B) \cdot P(B) = P(B|A) \cdot P(A)$

$P(A|B) = \frac{P(B|A)P(A)}{P(B)}$

$p(A|B)$ -> 사후 확률. (B라는 정보가 업데이트 된 이후의 사(이벤트)후 확률)
$p(A)$ -> 사전 확률. B라는 정보가 업데이트 되기 전의 사전확률
$p(B|A)$ -> likelihood

예시
위키피아
약물을 실제 사용 하는 경우 결과가 양성일 확률은 99%
만약 1%의 위양성 (False positive, 실제로 약물이 없지만 양성반응이 나타남)이 존재하는 경우에도 테스트의 의미는 매우 크게 바뀝니다.
실제 분석을 위해, 전체 인구에서 0.5%, ( 1/200 ) 만이 실제로 약물이 신체에 포함되어 있다고 가정해보도록 하겠습니다.
양성반응 테스트의 결과가 양성으로 나왔을 경우 실제로 약물이 있을 확률은 어느정도가 될까요?

• TPR : True Positive Rate (= 민감도, true accept rate) 1인 케이스에 대해 1로 잘 예측한 비율.(암환자를 암이라고 진단 함)
• FPR : False Positive Rate (= 1-특이도, false accept rate) 0인 케이스에 대해 1로 잘못 예측한 비율.(암환자가 아닌데 암이라고 진단 함)

계산

p_pos_used = 0.99  # True positive rate (TPR, Sensitivity)
p_used = 0.005  # prior probability
p_pos_not_used = 0.01  # False positive rate (FPR)
p_not_used = 1 - p_used  # 1 - p_used  
numerator = p_pos_used * p_used 
denominator = (p_pos_used * p_used) + (p_pos_not_used * p_not_used)
posterior_probability = numerator / denominator
posterior_probability

이후 또 시행하게 된다면 p_used만 제외하고 나머지는 같은 값
p_used는 이전에 시행된 결과값 사용