모수적 기법과 비모수적 기법

모수적 기법 (parametric)

1. 추정해야할 계수의 수가 적기 때문에 적합하기가 쉽다.
2. 계수들에 대한 해석이 간단하고 통계적 유의성을 쉽게 검정할 수 있다.
3. f(X)의 형태에 대한 강한 가정을 근거로 구성된다.

ex. 선형회귀, 로지스틱회귀모델, 1차/2차 판별모델

비모수적 기법 (non-parametric)

1. 모수적 형태를 명시적으로 가정하지 않고, 그렇게 함으로써 더욱 유연한 또 다른 회귀 기법을 제공한다
2. 선택된 모수의 형태가 모수적 기법에 가깝지 않은 경우 비모수적 기법의 성능이 훨씬 좋다.
3. 비모수적 기법이 초래한 분산 증가는 편향 감소로 상쇄되지 않는다.

ex. K-최근접이웃회귀(KNN 분류기와 밀접한 관련이 있음), 의사결정나무, 랜덤포레스트

KNN 적합의 예시

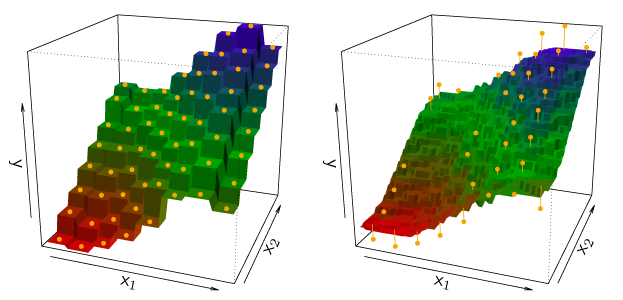위의 그래프는 설명변수가 2개인 데이터셋에 대한 두 개의 KNN 적합을 보여준다. KNN 적합은 훈련 관측치를 완벽하게 보간하고 K개 관측치의 평균을 이용하여 계단함수의 형태를 띈다. 왼쪽은 K=1, 오른쪽은 K=9인 경우이다. 최적의 K값은 편향-분산 절충(bias-variance trade off)에 따라 달라질 것이다. K 값이 작으면 적합이 유연해져서 편향은 낮지만, 분산이 클 것이다. K 값이 클수록 적합은 더 평활해지고 변동이 줄어든다.

인공신경망은 모수적 모델인가 비모수적 모델인가$?^{[1]}$

인공신경망 모델은 인풋, 은닉, 아웃풋 3개의 층(layer)으로 구성되어 있으며 각 층에 있는 노드들이 서로 연결된 네트워크 그래프 형태로 표현된다. 인공신경망 모델은 일단 네트워크 구조가 결정되면, 층간 노드들을 연결하고 있는 연결선의 가중치를 결정하는 것이 핵심이다. 여기에서 가중치는 모수(parameter)이며, 은닉층의 개수, 은닉층에 포함할 노드의 개수 등은 하이퍼모수(hyperparameter)이다. 모수인 가중치를 계산할 때 확률분포의 개념은 사용되지 않는다. 따라서 확률분포 사용 여부를 기준으로 본다면 인공 신경망은 비모수적 모델이다. 따라서 우리는 세미모수적 모델이라는 새로운 개념을 소개해보도록 하겠다.

세미모수적 기법 (semiparametric)

모수와 비모수의 중간으로, 연결선의 가중치인 모수가 존재하나 이 모수는 확률 분포와는 무관하게 얻어진다.
ex. 인공신경망, 서포트 벡터 머신

References
1. 모수 모델 vs 비모수 모델