자료구조 - Heap

1. Heap

힙(Heap)은 자료구조 중 하나로, 주로 우선순위 큐(Priority Queue)를 구현하는 데 사용되는 데이터 구조이다.

• 완전 이진 트리의 일종이다.
• 여러 값 중, 최대값과 최소값을 빠르게 찾아내도록 만들어진 자료구조로 반정렬 상태이다.
• 힙 트리는 중복된 값을 허용한다. (이진 탐색 트리는 중복값 허용X)
• BST(이진 탐색 트리)와 다르다. 좌, 우 자식의 위치가 대소 관계를 반영하지 않는다. (층(level)으로 대소 관계를 구분한다.)
• 왼쪽 자식과 오른쪽 자식은 부모 노드보다 작은 값을 유지하기만 하면 된다.

힙의 종류

1.최대 힙(Max Heap)

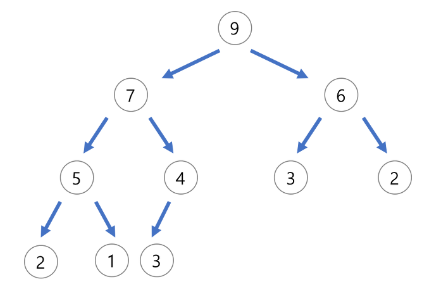
• Max Heap은 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리이다.
• 부모노드의 key >= 자식 노드의 key

2.최소 힙(Min Heap)

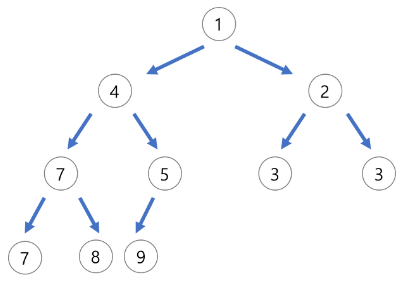
• Min Heap은 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리이다.
• 부모노드의 key <= 자식 노드의 key

Heapify
Heapify는 힙을 고친다라는 의미로 현재 삽입 혹은 삭제될 노드에 의해 전체 정렬 상태에 영향이 생길 경우 그 정렬을 다시 올바르게 진행하기 위한 절차를 의미한다.

Heap 연산

1.힙의 삽입 연산

• 새로운 노드를 힙의 마지막 노드에 삽입한다.
• 새로운 노드를 부모 노드들과 교환해 힙의 성질을 만족시킨다.

삽입 연산의 시간 복잡도는 O(log n)이다.

2.힙의 삭제 연산
힙의 삭제 연산은 언제나 루트 노드에 있는 원소를 삭제하여 반환한다. 따라서 루트 노드를 삭제하고 다시 트리를 힙의 조건으로 유지시켜주어야 한다.

• 힙의 루트 노드를 삭제 후 반환
• 마지막 노드를 루트 노드로 이동
• 힙의 조건에 맞게 트리를 재 조정

삭제 연산의 시간 복잡도는 O(log n)이다.

Heap 구현

먼저 힙 자료구조를 트리와 배열로 보자

MaxHeap

package com.example.datastructure.Heap;

import java.util.Arrays;
import java.util.Collections;

public class MaxHeap<T extends Comparable<T>> implements IHeap<T> {
    T[] data;
    int size;
    int maxSize;

    public MaxHeap(int maxSize) {
        this.maxSize = maxSize;
        this.data = (T[]) new Comparable[maxSize + 1];
        this.size = 0;
    }

    private int parent(int pos) {
        return pos / 2;
    }

    private int leftChild(int pos) {
        return (2 * pos);
    }

    private int rightChild(int pos) {
        return (2 * pos) + 1;
    }
    private boolean isLeaf(int pos) {
        return (pos > (size / 2) && pos <= size);
    }

    private void heapify(int idx) {
        if (isLeaf(idx)) {
            return;
        }

        T current = this.data[idx];
        T left = this.data[leftChild(idx)];
        T right = this.data[rightChild(idx)];

        if (current == null) {
            return;
        }

        if (current.compareTo(left) < 0 ||
                current.compareTo(right) < 0) {

            if (left.compareTo(right) > 0) {
                Collections.swap(Arrays.asList(this.data), idx, leftChild(idx));
                heapify(leftChild(idx));
            } else {
                Collections.swap(Arrays.asList(this.data), idx, rightChild(idx));
                heapify(rightChild(idx));
            }
        }
    }

    @Override
    public void insert(T val) {
        this.data[++this.size] = val;

        int current = this.size;
        while (this.data[parent(current)] != null &&
                this.data[current].compareTo(this.data[parent(current)]) > 0) {
            Collections.swap(Arrays.asList(this.data), current, parent(current));
            current = parent(current);
        }
    }

    @Override
    public boolean contains(T val) {
        for (int i = 1; i <= this.size; i++) {
            if (val.equals(this.data[i])) {
                return true;
            }
        }
        return false;
    }

    @Override
    public T pop() {
        T top = this.data[1];
        this.data[1] = this.data[this.size--];
        heapify(1);
        return top;
    }

    @Override
    public T peek() {
        if (this.size < 1) {
            throw new RuntimeException();
        }
        return this.data[1];
    }

    @Override
    public int size() {
        return this.size;
    }
}

관련 알고리즘 문제

1655. 가운데를 말해요.
      

설명이 편해진다.

• 리스트
  • 데이터가 들어올 때마다 정렬해야 됨
  • N * NlogN
• 우선순위 큐
  • 데이터가 들어올 때마다 데이터 삽입/삭제
  • N * (logN)

package com.example.datastructure.Heap;

import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Scanner;

/*
1655. 가운데를 말해요
 */

public class Baekjoon_1655 {
    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();

        PriorityQueue<Integer> min = new PriorityQueue<>();
        PriorityQueue<Integer> max = new PriorityQueue<>(Comparator.reverseOrder());

        StringBuilder result = new StringBuilder();
        for(int i = 0; i<N ; i++){
            int x = sc.nextInt();

            if(max.size() == min.size()){
                max.offer(x);
            }else{
                min.offer(x);
            }

            if(!min.isEmpty() && max.peek() > min.peek()){
                min.offer(max.poll());
                max.offer(min.poll());
            }
            result.append(max.peek() + "\n");
        }

        System.out.println(result.toString());
    }
}