자료구조 - Tree

1. 트리

트리 (Tree)란 노드들이 나무 가지처럼 연결된 비선형 계층적 자료구조입니다.

1. 트리 용어

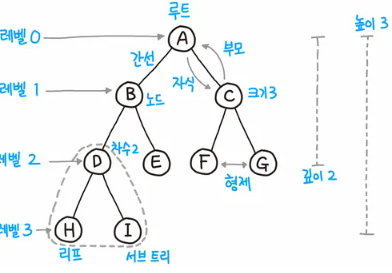
트리는 항상 루트(root)에서부터 시작된다. 루트는 자식(child) 노드를 가지며, 간선(edge)으로 연결되어 있다. 자식 노드의 개수는 차수(degree)라고 하며, 크기(size)는 자신을 포함한 모든 자식 노드의 개수다. 높이(height)는 현재 위치에서부터 리프(leaf)까지의 거리, 깊이(depth)는 루트에서부터 현재 노드까지의 거리다. 트리는 그 자식도 트리인 서브트리(subtree) 구성을 띤다. 레벨(level)은 0부터 시작한다.

• 노드(node): 트리를 구성하는 기본 원소
  • 루트 노드(root node/root): 트리에서 부모가 없는 최상위 노드, 트리의 시작점
  • 부모 노드(parent node): 루트 노드 방향으로 직접 연결된 노드
  • 자식 노드(child node): 루트 노드 반대방향으로 직접 연결된 노드
  • 형제 노드(siblings node): 같은 부모 노드를 갖는 노드들
  • 리프 노드(leaf node/leaf): 루트 노드를 제외한 차수가 1인 정점을 뜻한다. 쉽게 말해 자식이 없는 노드. 단말 노드라 부르기도 한다.
• 경로(path): 한 노드에서 다른 한 노드에 이르는 길 사이에 있는 노드들의 순서
• 길이(length): 출발 노드에서 도착 노드까지 거치는 간선의 개수
• 깊이(depth): 루트 경로의 길이
• 레벨(level): 루트 노드(level=0)부터 노드까지 연결된 간선 수의 합
• 높이(height): 가장 긴 루트 경로의 길이
• 차수(degree): 각 노드의 자식의 개수
• 크기(size): 노드의 개수
• 너비(width): 가장 많은 노드를 갖고 있는 레벨의 크기

2. 이진트리

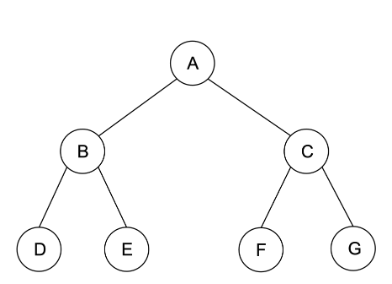
이진트리(Binary Tree)는 트리(Tree)의 일종으로, 각 노드가 최대 두 개의 자식 노드를 가지는 특별한 형태의 자료구조이다.

2-1. 완전 이진 트리

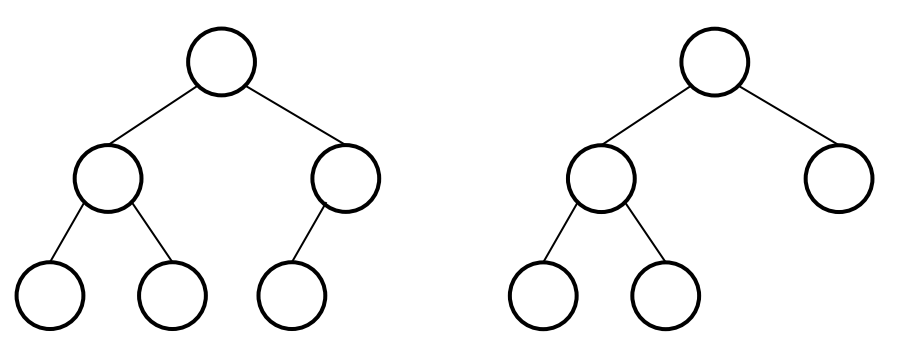
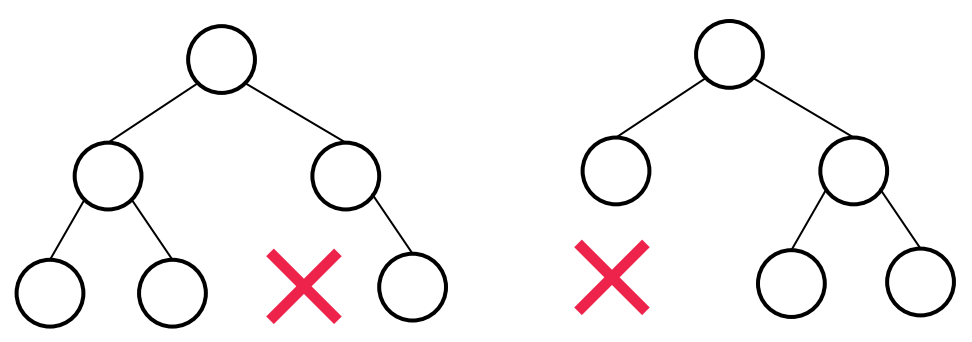
특징

• 마지막 레벨을 제외하고 모든 노드가 채워져야 함
• 노드는 왼쪽에서 오른쪽으로 채워짐
• 완전 이진트리는 배열을 사용해 효율적으로 표현 가능하다.
  

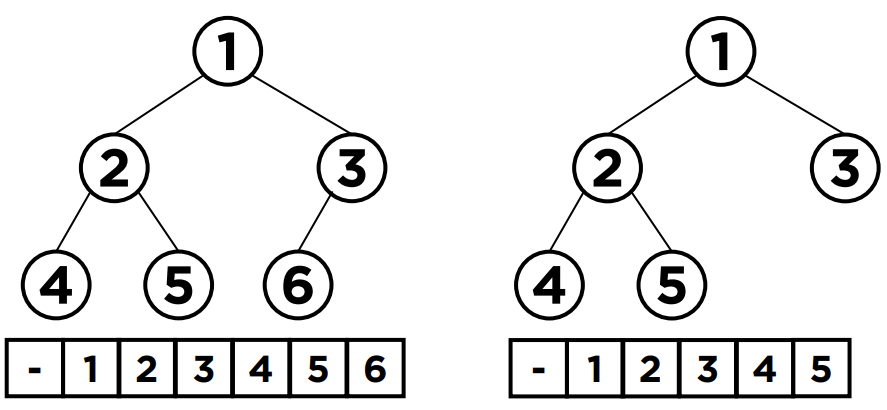
2-2. 포화 이진 트리

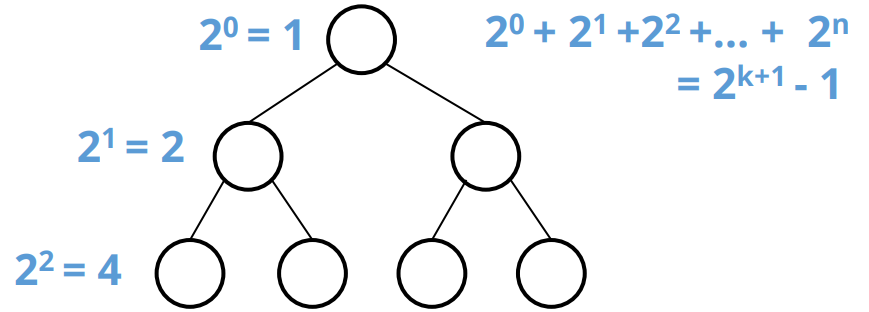
특징

• 모든 노드가 2개의 자식을 가지고 leaf 노드가 같은 레벨일 때
• 높이가 h인 포화 이진 트리에서 노드 갯수는 2^(k+1) – 1
• Leaf 노드의 갯수는 2^h

3. 트리 탐색

트리의 모든 노드들을 방문하는 과정을 트리 순회(TreeTraversal)라고 한다.
선형 자료 구조(연결 리스트, 스택, 큐 등)는 순차적으로 요소에 접근하지만 트리 자료구조는 다른 방식을 사용해야 합니다.

트리 순회 방식

• 전위 순회 (Preorder)
• 중위 순회 (Inorder)
• 후위 순회 (Postorder)

3-1. 전위 순회(Preorder)

• 트리를 복사하거나, 전위 표기법을 구하는데 주로 사용됩니다.
• 트리를 복사할때 전위 순회를 사용하는 이유는 트리를 생성할 때 자식 노드보다 부모 노드가 먼저 생성되어야 하기 때문입니다.

전위 순회는 다음과 같은 방법으로 진행한다.

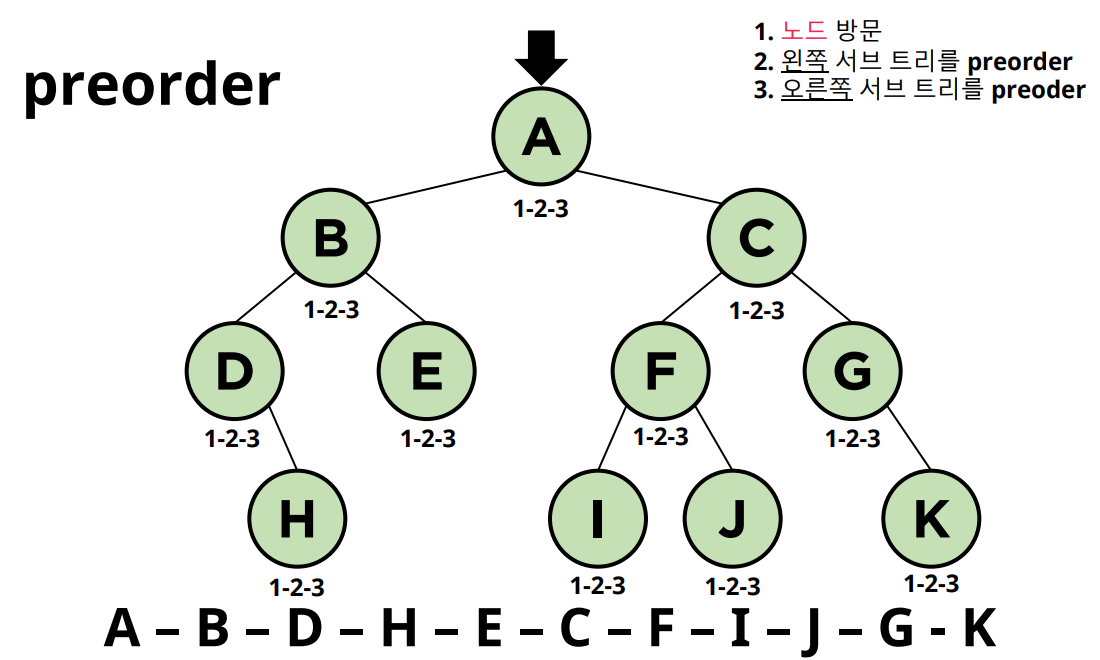
1. Root 노드를 방문한다.
2. 왼쪽 서브 트리를 전위 순회한다.
3. 오른쪽 서브 트리를 전위 순회한다.

3-2. 중위 순회 (Inorder)

• 중위 순회는 이진 탐색트리(BST)에서 오름차순 또는 내림차순으로 값을 가져올 때 사용됩니다.
• 내림차순으로 값을 가져오기 위해서는 역순(오른쪽-> root-> 왼쪽)으로 중위 순회를 하면 됩니다.

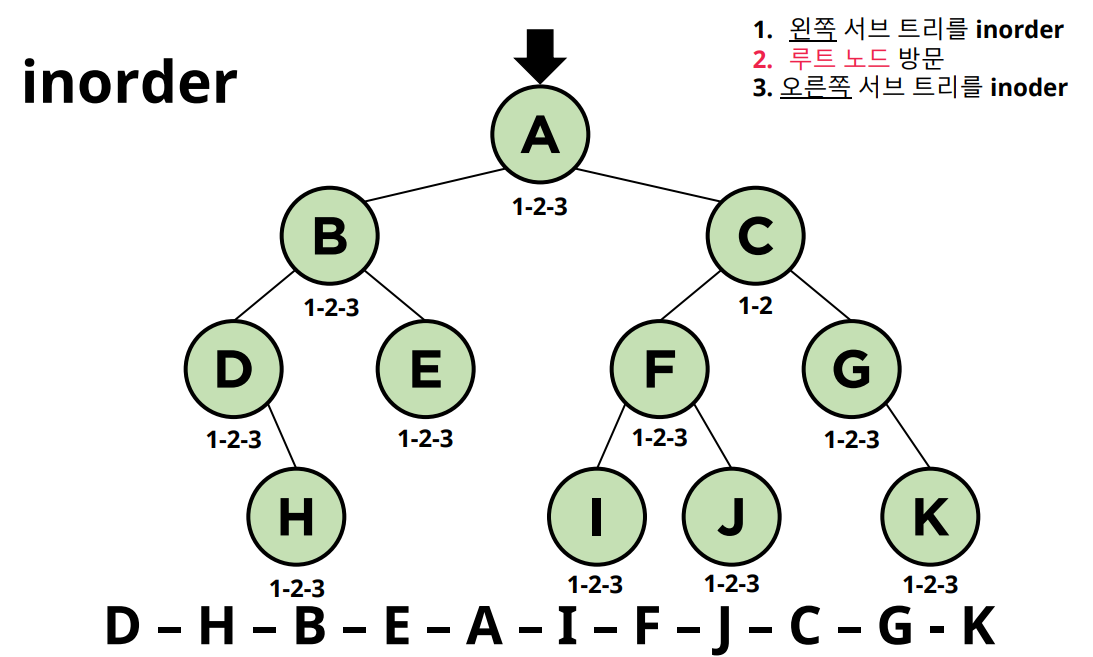
1. 왼쪽 서브 트리를 전위 순회한다.
2. Root 노드를 방문한다.
3. 오른쪽 서브 트리를 전위 순회한다.

3-3. 후위 순회 (Postorder)

• 후위 순회는 트리를 삭제하는데 주로 사용됩니다.
• 이유는 부모노드를 삭제하기 전에 자식 노드를 삭제하는 순으로 노드를 삭제해야 하기 때문입니다.

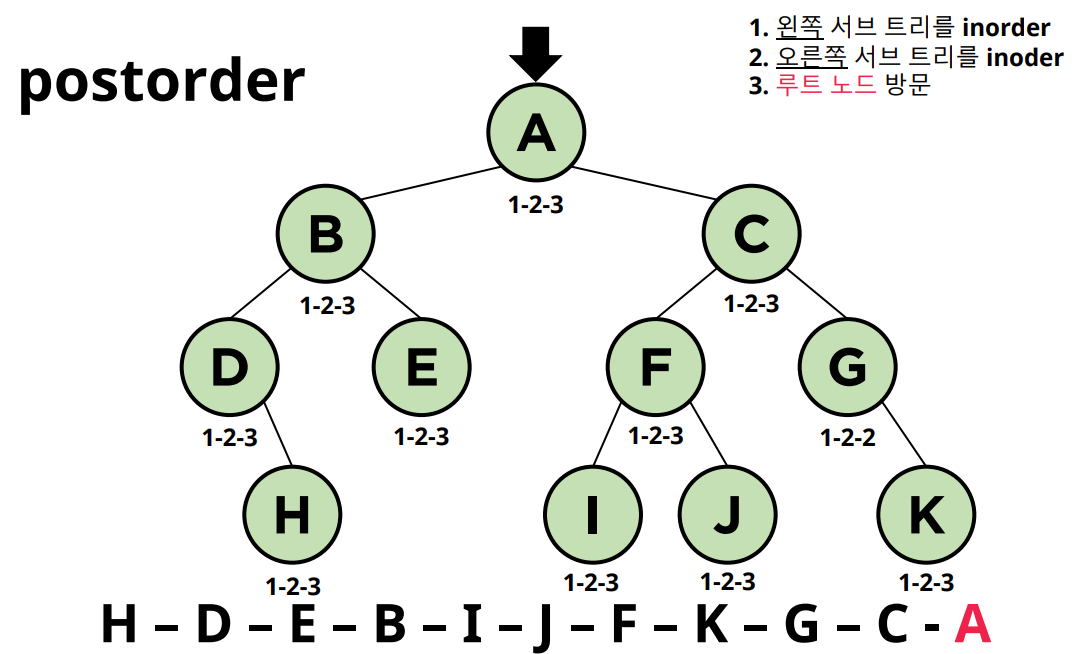
1. 왼쪽 서브 트리를 전위 순회한다.
2. 오른쪽 서브 트리를 전위 순회한다.
3. Root 노드를 방문한다.

4. 이진 트리 탐색(Binary Search Tree)

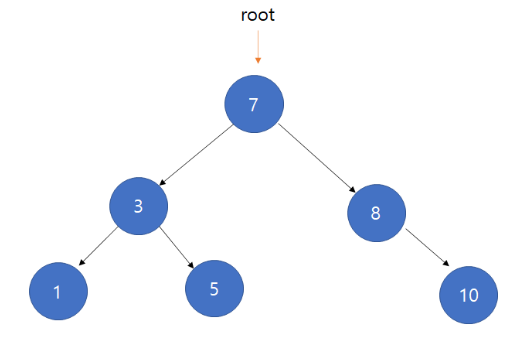
이진탐색트리란 다음과 같은 특징을 갖는 이진트리를 말한다.
1. 각 노드에 중복되지 않는 키(key)가 있다.
2. 루트노드의 왼쪽 서브 트리는 해당 노드의 키보다 작은 키를 갖는 노드들로 이루어져 있다.
3. 루트노드의 오른쪽 서브 트리는 해당 노드의 키보다 큰 키를 갖는 노드들로 이루어져 있다.
4. 좌우 서브 트리도 모두 이진 탐색 트리여야 한다.

4-1. 이진 트리 탐색 Java 구현

BinarySearchTree

package com.example.datastructure.Tree;

import java.util.ArrayList;
import java.util.List;

public class BinarySearchTree<T extends Comparable<T>> implements ITree<T> {

    private Node root;
    private int size;

    public BinarySearchTree() {
        this.size = 0;
    }

    @Override
    public void insert(T val) {
        this.root = insertNode(root, val);
        size++;
    }

    @Override
    public void delete(T val) {
        deleteNode(root, val);
    }

    private Node deleteNode(Node node, T val) {
        if (node == null) {
            return null;
        }

        if (val.compareTo(node.data) < 0) {
            node.left = deleteNode(node.left, val);
        } else if (val.compareTo(node.data) > 0) {
            node.right = deleteNode(node.right, val);
        } else {
            this.size--;
            if (node.left == null) {
                return node.right;
            } else if (node.right == null) {
                return node.left;
            }
            node.data = minNode(node.right);
            node.right = deleteNode(node.right, node.data);
        }
        return node;
    }

    public T min() {
        return this.minNode(this.root);
    }

    public T max() {
        return this.maxNode(this.root);
    }

    private T minNode(Node node) {
        T minData = node.data;
        while (node.left != null) {
            minData = node.left.data;
            node = node.left;
        }
        return minData;
    }

    private T maxNode(Node node) {
        T maxData = node.data;
        while (node.right != null) {
            maxData = node.right.data;
            node = node.right;
        }
        return maxData;
    }

    private Node insertNode(Node node, T val) {
        if (node == null) {
            return new Node(val);
        }
        // a.compareTo(b) 는 a 가 b 보다 작으면 -1 을 리턴
        // 동일할 때 0 , b 가 더 크면 1을 리턴
        if (val.compareTo(node.data) < 0) {
            // 추가될 값이 노드의 데이터 보다 작은 경우 노드의 왼쪽에 위치 해야 함
            node.left = insertNode(node.left, val);
        } else if (val.compareTo(node.data) > 0) {
            // 추가될 값이 노드의 데이터 보다 큰 경우 노드의 오른쪽 위치 해야 함
            node.right = insertNode(node.right, val);
        }

        return node;
    }

    @Override
    public boolean contains(T val) {
        return containsNode(root, val);
    }

    @Override
    public int size() {
        return this.size;
    }

    private boolean containsNode(Node node, T val) {
        if (node == null) {
            return false;
        }
        
        // a.compareTo(b)
        // a < b   --> return -1
        // a == b  --> return 0
        // a > b   --> return 1

        if (val.compareTo(node.data) == 0) {
            return true;
        }

        if (val.compareTo(node.data) < 0) {
            return containsNode(node.left, val);
        }

        return containsNode(node.right, val);
    }

    public List<T> preOrder() {
        return preOrderTree(root, new ArrayList<>());
    }

    private List<T> preOrderTree(Node node, List<T> visited) {
        if (node == null) return visited;

        visited.add(node.data);
        preOrderTree(node.left, visited);
        preOrderTree(node.right, visited);

        return visited;
    }

    public List<T> inOrder() {
        return inOrderTree(root, new ArrayList<>());
    }

    private List<T> inOrderTree(Node node, List<T> visited) {
        if (node == null) return visited;

        inOrderTree(node.left, visited);
        visited.add(node.data);
        inOrderTree(node.right, visited);

        return visited;
    }

    public List<T> postOrder() {
        return postOrderTree(root, new ArrayList<>());
    }

    private List<T> postOrderTree(Node node, List<T> visited) {
        if (node == null) return visited;

        postOrderTree(node.left, visited);
        postOrderTree(node.right, visited);
        visited.add(node.data);

        return visited;
    }

    private class Node {
        T data;
        Node left;
        Node right;

        Node(T data) {
            this.data = data;
        }

        Node(T data, Node left, Node right) {
            this.data = data;
            this.left = left;
            this.right = right;
        }
    }
}

4-2. Insert

삽입 과정

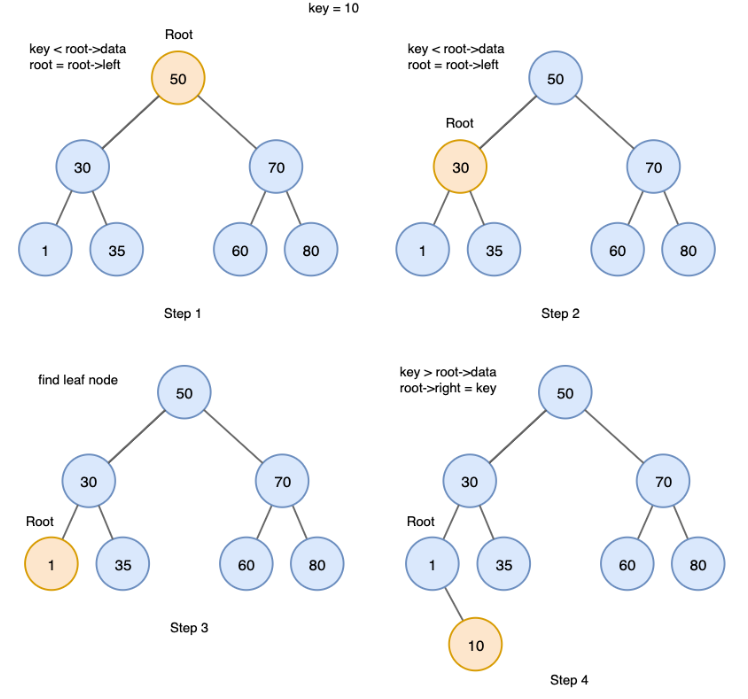
• Root에서 시작합니다.
• 삽입 값을 루트와 비교합니다. 루트보다 작으면 왼쪽으로 재귀하고 크다면 오른쪽으로 재귀합니다.
• 리프 노드에 도달한 후 노드보다 크다면 오른쪽에 작다면 왼쪽에 삽입합니다.

    private Node insertNode(Node node, T val) {
        if (node == null) {
            return new Node(val);
        }
        // a.compareTo(b) 는 a 가 b 보다 작으면 -1 을 리턴
        // 동일할 때 0 , b 가 더 크면 1을 리턴
        if (val.compareTo(node.data) < 0) {
            // 추가될 값이 노드의 데이터 보다 작은 경우 노드의 왼쪽에 위치 해야 함
            node.left = insertNode(node.left, val);
        } else if (val.compareTo(node.data) > 0) {
            // 추가될 값이 노드의 데이터 보다 큰 경우 노드의 오른쪽 위치 해야 함
            node.right = insertNode(node.right, val);
        }

        return node;
    }

4-3. Delete

세가지 상황이 있다.

1. 삭제할 노드가 리프노드인 경우
   

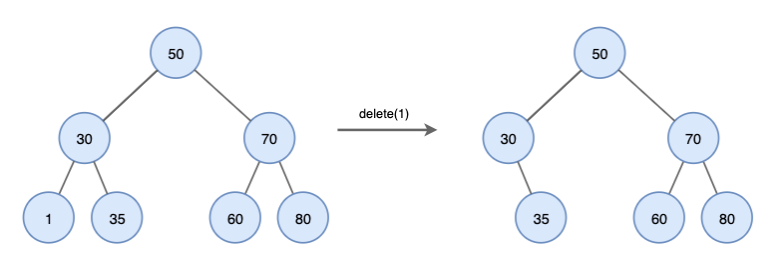
• 노드를 삭제하기만 하면 된다.

2. 삭제할 노드에 자식이 하나만 있는 경우
   

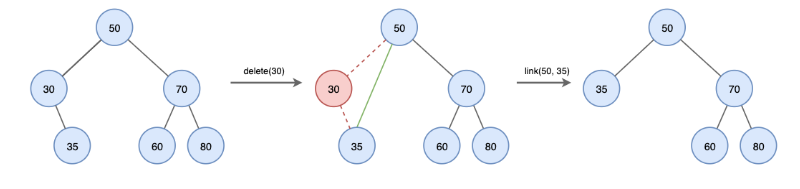
• 노드를 삭제하고 자식 노드를 삭제된 노드의 부모에 직접 연결한다.

3. 삭제할 노드에 자식이 둘 있는 경우
   

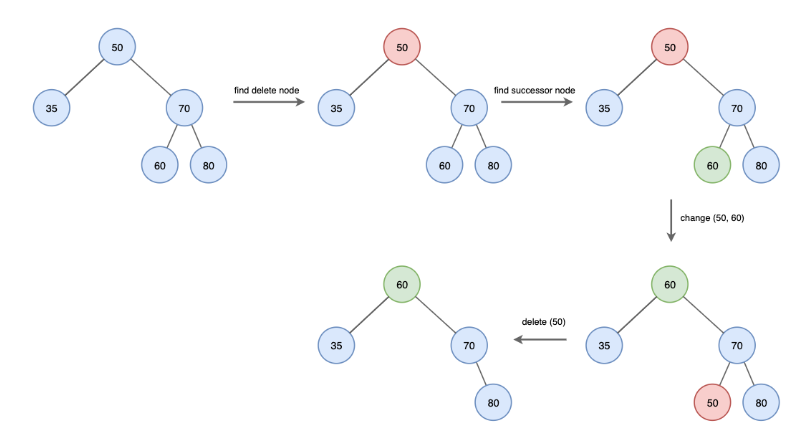
• 자식이 둘 있는 경우 successor 노드를 찾는 과정이 추가
• 삭제할 노드를 찾습니다.
• 삭제할 노드의 successor 노드를 찾습니다.
• 삭제할 노드와 successor 노드의 값을 바꿉니다.
• successor 노드를 삭제합니다.

    private Node deleteNode(Node node, T val) {
        if (node == null) {
            return null;
        }

        if (val.compareTo(node.data) < 0) {
            node.left = deleteNode(node.left, val);
        } else if (val.compareTo(node.data) > 0) {
            node.right = deleteNode(node.right, val);
        } else {
            this.size--;
            if (node.left == null) {
                return node.right;
            } else if (node.right == null) {
                return node.left;
            }
            node.data = minNode(node.right);
            node.right = deleteNode(node.right, node.data);
        }
        return node;
    }

4-4. contains

    private boolean containsNode(Node node, T val) {
        if (node == null) {
            return false;
        }

        // a.compareTo(b)
        // a < b   --> return -1
        // a == b  --> return 0
        // a > b   --> return 1

        if (val.compareTo(node.data) == 0) {
            return true;
        }

        if (val.compareTo(node.data) < 0) {
            return containsNode(node.left, val);
        }

        return containsNode(node.right, val);
    }

관련 알고리즘 문제

9934. 완전 이진 트리

package com.example.datastructure.Tree;


import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;


/*
9934. 완전 이진 트리
 */

public class Baekjoon_9934 {
    static int K;
    static int[] arr;
    static StringBuffer[] ans;

    public static void main(String[] args) throws Exception {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        K = Integer.parseInt(br.readLine());
        arr = new int[(int) Math.pow(2, K) - 1];

        String[] input = br.readLine().split(" ");
        for (int i = 0; i < arr.length; i++)
            arr[i] = Integer.parseInt(input[i]);

        ans = new StringBuffer[K];
        for (int i = 0; i < K; i++)
            ans[i] = new StringBuffer();

        solve(0, arr.length - 1, 0);

        for (int i = 0; i < K; i++)
            bw.write(ans[i].toString() + "\n");
        bw.flush();

    }

    public static void solve(int s, int e, int floor) {

        if (floor == K)
            return;

        int m = (s + e) / 2;
        ans[floor].append(arr[m] + " ");

        solve(s, m - 1, floor + 1);
        solve(m + 1, e, floor + 1);
    }
}