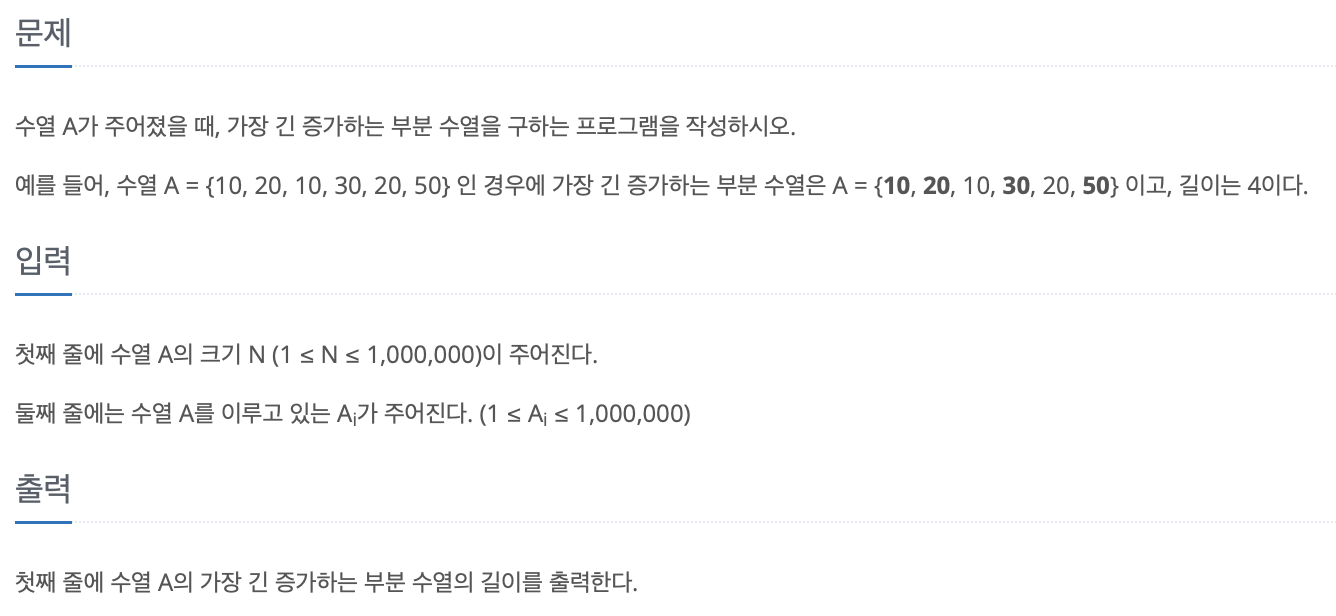
문제
https://www.acmicpc.net/problem/12015
풀이
이 문제는 dp를 이용해서 풀면 시간초과가 날 수 있다.
이분탐색을 이용해서 dp에 증가하는 수열을 최신화 하면서 생성한다.
dp의 첫번째 수는 arr의 첫번째 수를 넣어놓고 시작한다.
arr[i]가 dp[-1](dp의 마지막 수 보다)보다 크다면 그냥 dp에 넣으면 된다.
arr[i]가 dp[-1](dp의 마지막 수 보다)보다 작거나 같다면 dp에서 arr[i]가 들어갈곳을 찾아 arr[i]로 교체한다.
arr : 1, 2, 6, 3, 5, 6
1번째 arr[0] = 1)
dp : 1
2번째 arr[1] = 2) dp의 마지막 수(1)가 arr[1]보다 작기때문에 그냥 dp에 추가한다.
dp : 1, 2
3번째 arr[2] = 6) dp의 마지막 수(2)가 arr[2]보다 작기때문에 그냥 dp에 추가한다
dp : 1, 2, 6
4번째 arr[3] = 3) dp의 마지막 수(6)이 arr[3]보다 크기때문에 dp에 arr[3]이 들어갈 곳(index : 2)을 찾아 그곳과 교체한다.
dp : 1, 2, 3
이렇게 arr[5]까지 수행해 주면 dp : 1, 2, 3, 5, 6가 될것이다. 즉 dp의 길이가 최대 증가 수열의 길이이다.
코드
import bisect
from sys import stdin
input = stdin.readline
n = int(input())
arr = list(map(int,input().split()))
dp = [arr[0]]
for i in range(n):
if arr[i]>dp[-1]:
dp.append(arr[i])
else:
idx = bisect.bisect_left(dp, arr[i])#arr[i]가 들어갈 곳을 반환
dp[idx] = arr[i]#dp의 값과 arr[i]를 교환
print(len(dp))참고
비슷한 문제
11055번 : 가장 큰 증가 부분 수열 / 풀이
11053번 : 가장 긴 증가하는 부분 수열 / 풀이
11054번 : 가장 긴 바이토닉 부분 수열 / 풀이
