네트워크 유량

네트워크 유량이란 유방향 그래프에 용량이 존재하는 것이다. 유량의 시작 정점을 Source, 끝 정점을 Sink라고 한다.
이 때, Source에서 Sink로 흘려보낼 수 있는 최대 유량(flow)을 구하는 문제를 네트워크 유량 문제라고 한다.
유량(flow): 두 정점 사이에서 현재 흐르는 양용량(capacity): 두 정점 사이에 최대로 흐를수 있는 양잔여 용량(residual capacity): 두 정점 사이에서 현재 더 흐를 수 있는 유량. (용량 - 유량)소스(source): 유량이 시작되는 정점. 보통 S로 표현싱크(sink): 유량이 도착하는 정점. 보통 T로 표현증가 경로(augmenting path): S에서 T로 유량이 흐르는 경로

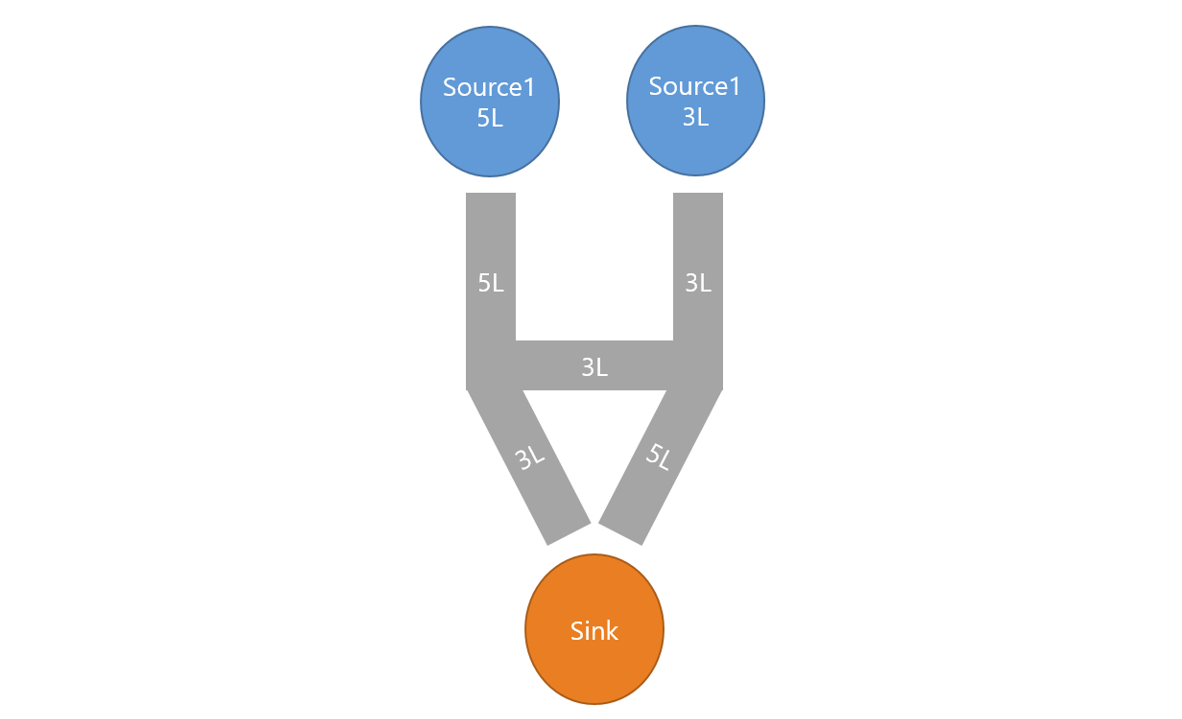
위 이미지와 같은 네트워크 유량이 있다고 하자.
S에서 1로 갈 수 있는 유량은 2, 2로 갈 수 있는 유량은 3이다.
S에서 1로 2만큼 유량이 흘러갔다면, 1에서 T로 용량은 3이지만 S에서 1로 흘러 들어온 2만큼만 유량을 보낼 수 있다.
마찬가지로, S에서 2로 갈 수있는 유량은 3이라 3을 흘려 보냈더라도 2에서 T로 흐를 수 있는 용량이 2라서 2만큼만 유량을 보낼 수 있다.
결과적으로 위 그래프는 S에서 T로 4를 흘러보내주게 되고, 최대 유량이 4라고 한다.
네트워크 유량 문제가 성립하기 위해서는 3가지 약속이 있다.
일단 네트워크 유량에서는 위에서" S에서 1로 갈 수 있는 유량은 2, 2로 갈 수 있는 유량은 3이다"
라는 표현을 c(S,1) = 2, c(S,2) = 3 이라고 간단하게 표현할 수 있다.
c(u,v):capacity정점 u에서 v로 가는 간선의 용량f(u,v):flow정점 u에서 v로 실제 흐르는 유량r(u,v):residual정점 u에서 v로 가는 잔여 용량r(u,v)=c(u,v)-f(u,v)
1) 용량 제한 속성 f(u,v) <= c(u,v) :
두 간선 사이에서 흐르는 유량은 용량을 넘을 수 없다.
2) 유량의 대칭성 f(u,v) = -f(v,u) :
u->v로 2만큼 흐른다면, v->u엔 -2만큼 흐른다.
쉽게 생각하면, 'u->v로 2만큼 나가고 v->u로 2만큼 들어온다.' 라고 이해하면 된다.
3) 유량 보존의 법칙 ∑f(u,v) = 0 :
S 와 T를 제외하고는 각 정점에서 들어오는 유량과 나가는 유량이 일치해야 한다.
그래서 유량의 대칭성 때문에 S와 T를 제외하고 유량을 모두 합하면 0이 되어야 한다.
포드-풀커슨 알고리즘
최초의 네트워크 유량 알고리즘
개념과 구현이 간단하다.
개념
- 각 간선의 용량을 입력받는다.
- DFS(포드-풀커슨)를 이용하여
r(u,v)> 0인 증가 경로를 찾는다. (DFS 기 때문에 최단경로 아님 ) - 찾은 증가 경로 상에서
r(u,v)이 가장 낮은 엣지를 찾는다. - 찾은 엣지의
r(u,v)만큼만 S에서 T까지 유량을 흘려보낸다(경로의 모든 엣지에 유량 추가). - 더 이상 증가 경로가 발견이 되지 않을 때까지 반복한다.
아래 그래프를 가지고 포드-풀커슨 알고리즘의 과정을 살펴 보면,

S->a->T 라는 증가 경로를 먼저 찾고, 그 다음 S->b->T라는 증가 경로를 찾아서 최대 유량을 찾을 수도 있다.

하지만, 만약 S->a->b->T라는 증가 경로를 가장 먼저 찾았는데, 이때 흘려 보낼수 있는 플로우는 1을 보내고 나니 그 다음 유량을 흘려 보낼 수 있는 루트를 찾아보니 없다.
여기서 위에서 살펴 보았던 2) 유량의 대칭성 f(u,v) = -f(v,u)의 개념이 이용된다.
현재 c(a,b)는 1이다. 그리고 c(b,a)는 경로가 존재하지 않으니 0이다.
그리고 f(a,b)도 방금 S->a->b->T 라는 증가 경로로 유량이 흘렀기 때문에 1이 되고, 유량의 대칭성에 의해서 f(b,a)은 -1이 된다.

그러면 놀랍게도 잔여 용량 r(b,a)(c(b,a) - f(b,a))은 0 - (-1)로, b에서 a로 흐르는 잔여 용량이 1이 된다.
즉, 유량의 하나 보내는 것은 반대로 유량을 하나 보낼 수 있는 작업이 동반된다고 생각하면 된다.
이렇게 Back-Edge라고 불리는 역간선 덕분에 포드-풀커슨 알고리즘이 성립 가능하게 된다.
그러면 결과적으로는 어떤 경로를 선택하든 최대 유량을 구할 수 있다.
시간복잡도
증가경로 한개당 플로우 1밖에 보낼 수 없다.
그래서 DFS를 플로우 수만큼 사용해야 하는데 플로우 수가 크다면 스택오버플로우가 발생할 수 있다.
시간복잡도는 O((V+E)F) 인데, E가 V를 도미넌트 하므로 보통 O(EF)라고 표현한다.
코드
최대 유량 : 백준 6086문제의 포드-풀커슨 알고리즘 풀이이다.
import java.io.*;
import java.util.*;
/*
* 메모리 시간
* 14388 140
*/
public class BaekOJ6086_배문규_DFS {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StringBuilder sb = new StringBuilder();
static StringTokenizer st = null;
static final int MAX_SIZE = 52;
static int N, maxFlow, S, T = 25, capacity[][], flow[][];
static boolean check[];
public static void main(String[] args) throws NumberFormatException, IOException {
capacity = new int[MAX_SIZE][MAX_SIZE];
flow = new int[MAX_SIZE][MAX_SIZE];
check = new boolean[MAX_SIZE];
N = Integer.parseInt(br.readLine());
for(int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
int start = charToInt(st.nextToken().charAt(0));
int end = charToInt(st.nextToken().charAt(0));
int weight = Integer.parseInt(st.nextToken());
// 여기서는 그냥 연결이기 때문에 무향 그래프라서 양방향으로 웨이트를 둘 다 더해줌
capacity[start][end] += weight;
capacity[end][start] += weight;
}
// 더 이상 증가경로가 없을 때 까지 반복
while(true) {
// 방문 체크 초기화
Arrays.fill(check, false);
// DFS로 최대 유량 찾기
int flowAmount = dfs(S, Integer.MAX_VALUE);
if(flowAmount == 0) break;
maxFlow += flowAmount;
}
System.out.println(maxFlow);
}
public static int dfs(int from, int amount) {
// 증가경로가 완성되면 해당 증가경로의 최소 잔여용량 리턴
if(from == T) return amount;
// 방문한 곳이면 리턴
if(check[from]) return 0;
check[from] = true;
for(int to = 0; to < MAX_SIZE; to++) {
// 유량이 흐를 수 있으면
if(capacity[from][to] > flow[from][to]) {
// 현재 도달한 경로까지의 최소 잔여용량 저장
int flowAmount = dfs(to, Math.min(amount, capacity[from][to]-flow[from][to]));
if(flowAmount > 0) {
// 잔여용량 갱신하고 리턴
flow[from][to] += flowAmount;
flow[to][from] -= flowAmount;
return flowAmount;
}
}
}
return 0;
}
// 문자를 인덱스로 매핑하기 위해 변환
public static int charToInt(char c) {
if('a' <= c && c <= 'z') c -= 6;
return c - 65;
}
}에드몬드-카프 알고리즘
앞서 살펴본 포드-풀커슨 알고리즘은 임의의 유량 그래프가 주어졌을 때, 원래 경로가 이미 사용되어 막혀있어도 Back-Edge 덕분에 최대 유량은 확실하게 구할 수 있다는 것을 알게되었다.
하지만 최대 유량만 알 수 있지, 우리가 생각하는 유량이 흐르는 실제 경로를 제시하지는 않는다.
아래 유량 그래프를 다시 한 번 예시로 보자.

포드-풀커슨 알고리즘에서는 S->1->2->T 가 먼저 증가경로로 잡히면, 유량의 대칭성으로 잔여 유량이 1이 생겨 2->1로 갈 수 있는 경로가 생겨서 S->2->1->T라는 증가경로가 생기게 되어서
- S->1->2->T (유량 1 보냄)
- S->2->1->T (유량 1 보냄)
- S->1->2->T (유량 1 보냄)
- S->2->1->T (유량 1 보냄)
- 최대 유량 : 4
이런 방식으로 결국 최대 유량을 알게되었다. 그래서 총 4번의 증가경로 탐색이 필요하다.
이렇기 때문에 위 그래프와 같이 중간에 용량이 1인 엣지가 끼어있는 병목상태에서는 포드-풀커슨 알고리즘은 굉장히 비효율적으로 동작할 수 있다.
하지만 실제 유량이 흐르는 증가경로는 아래와 같다.
- S->1->T (유량 2 보냄)
- S->2->T (유량 2 보냄)
- 최대 유량 : 4
위 방식처럼 동작하는 알고리즘이 바로 에드먼드-카프 알고리즘이다.
포드-풀커슨 알고리즘이 DFS 방식으로 증가경로를 탐색했다면, 에드먼드-카프 알고리즘은 BFS 방식으로 증가경로를 탐색한다.
가장 짧은 경로의 증가 경로를 탐색하여 해당 증가경로로 보낼 수 있는 최대의 유량을 한번에 보내면 된다.
즉, 최단거리로 최대의 유량을 보내기 때문에 중간에 용량이 1인 엣지가 끼어있어도 돌아가는 길이라면 무시할 수 있는 것이다.
잔여용량이 남은 간선들만을 이용해서 BFS를 반복적으로 수행하고, 찾은 경로들에게 유량을 보내고, 더이상 할 수 없을때까지 보낸 총 유량을 반환하기만 하면 된다.
개념
- 각 간선의 용량을 입력받는다.
- BFS(에드몬드-카프)를 이용하여
r(u,v)> 0인 증가 경로 중 최단 거리를 찾는다. - 찾은 증가 경로 중에서
r(u,v)이 가장 낮은 엣지를 찾는다. - 찾은 엣지의
r(u,v)만큼만 S에서 T까지 유량을 흘려보낸다(경로의 모든 엣지에 유량 추가). - 더 이상 증가 경로가 발견이 되지 않을 때까지 반복한다.
시간복잡도
BFS 한번이 O(E)이고, 증가 경로를 최대 VE번 찾기 때문에 에드먼드-카프 알고리즘의 일반적으로 알려진 시간복잡도는 O(VE^2)라고 한다.
증가 경로를 최대 VE번 찾는 이유(복잡함)에 대한 더 이상의 자세한 설명은 생략한다.
정확하게는 min(O(|E|f), O(VE^2))라고 하는데 만약 간선은 많고, 흘러야 하는 유량이 적을 때는 O(|E|f) < O(VE^2)이 될 수 있다고 한다.
코드
최대 유량 : 백준 6086문제의 에드몬드-카프 알고리즘 풀이이다.
import java.io.*;
import java.util.*;
/*
* 메모리 시간
* 14208 136
*/
public class BaekOJ6086_배문규_BFS {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StringBuilder sb = new StringBuilder();
static StringTokenizer st = null;
static final int MAX_SIZE = 52;
static int N, maxFlow, S, T = 25, aPath[], capacity[][], flow[][];
static Queue<Integer> queue;
public static void main(String[] args) throws NumberFormatException, IOException {
capacity = new int[MAX_SIZE][MAX_SIZE];
flow = new int[MAX_SIZE][MAX_SIZE];
N = Integer.parseInt(br.readLine());
for(int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
int start = charToInt(st.nextToken().charAt(0));
int end = charToInt(st.nextToken().charAt(0));
int weight = Integer.parseInt(st.nextToken());
// 여기서는 그냥 연결이기 때문에 무향 그래프라서 양방향으로 웨이트를 둘 다 더해줌
capacity[start][end] += weight;
capacity[end][start] += weight;
}
queue = new ArrayDeque<Integer>();
aPath = new int[MAX_SIZE];
// 더 이상 증가경로가 없을 때 까지 반복
while(true) {
// 큐, 증가경로 초기화
queue.clear();
Arrays.fill(aPath, -1);
aPath[S] = S;
queue.add(S);
// BFS로 최단거리 증가경로 찾기
while(!queue.isEmpty() && aPath[T] == -1) {
int from = queue.poll();
for(int to = 0; to < MAX_SIZE; to++) {
// 유량이 흐를 수 있으면서, 아직 방문하지 않았다면
if(capacity[from][to] > flow[from][to] && aPath[to] == -1) {
queue.offer(to);
aPath[to] = from;
}
}
}
// 경로가 없으면 종료
if(aPath[T] == -1) break;
// 찾은 증가 경로의 r(u,v)의 최솟값 (최소 잔여 용량)을 찾음
int flowAmount = Integer.MAX_VALUE;
for(int i = T; i != S; i = aPath[i])
flowAmount = Math.min(capacity[aPath[i]][i] - flow[aPath[i]][i], flowAmount);
for(int i = T; i != S; i = aPath[i]) {
flow[aPath[i]][i] += flowAmount; // 경로들에 유량 흘러줌
flow[i][aPath[i]] -= flowAmount; // 유량의 대칭성으로 반대 경로에 - 유량 흘림
}
maxFlow += flowAmount;
}
System.out.println(maxFlow);
}
// 문자를 인덱스로 매핑하기 위해 변환
public static int charToInt(char c) {
if('a' <= c && c <= 'z') c -= 6;
return c - 65;
}
}
이분 매칭
이분 매칭(Bipartite Matching) 알고리즘은 네트워크 유량 알고리즘과 연계되는 개념으로, 이분 그래프에서 두 그룹간의 최대 매칭을 의미한다.
즉,
집단 A가집단 B를 선택하는 방법에 대한 알고리즘이다.
먼저 이분 그래프란, 전체 그래프에서 점 들을 두 그룹으로 나누었을 때, 같은 그룹내에는 간선이 존재하지 않게 나눌 수 있는 그래프를 의미한다.
그래프를 나눌 수 있는 경우가 여러가지 있을 수 있지만, 보통 문제에서는 명확히 두 그룹을 분류해주는 경우가 많다.
개념
아래 예시를 통해 이분 매칭의 개념을 대해 알아보도록 하자.
네이버 클라우드, 카카오, 삼성전자에 각각 1자리씩 TO가 났고, 위 세 기업에 모두 최종 합격한 3명의 스터디원들이 있다.

위 예시에서는 집단 A가 스터디원 들이고, 집단 B는 기업 이라고 할 수 있다.
이와 같이 각 스터디원들이 희망하는 기업들이 미리 정해져 있을 때, 스터디원들이 희망 기업으로 입사하는 경우를 이분 매칭으로 알아보자.
먼저, 위 경우를 아래와 같은 그래프로 표현할 수 있다.

이분 매칭은, 두개의 그래프를 최대한으로 연결시켜주는 최대 연결(매칭)을 의미한다.
즉, 최대한 많은 스터디원들이 희망 기업으로 입사하는 경우를 찾는 문제로 볼 수 있다. 뭔가 느낌이 오지 않는가?
우리가 그전까지 살펴본 네트워크 유량 문제 또한 Source에서 Sink로 흘려보낼 수 있는 최대 유량(flow)을 구하는 문제이고,
이분 매칭 문제 또한 A에서 B로 갈 수 있는 최다 경우를 구하는 문제이기 때문에, 아래와 같이 이분 매칭을 네트워크 유량으로 표현할 수 있다.

위와 같이 선택을 1가지만 할 수 있는 이분 매칭은 모든 엣지의 용량이 1로 설정된 네트워크 유량 문제로 이해할 수 있다.
우리가 직전에 보았던 에드몬드-카프 알고리즘은 보통 시간 복잡도가 O(V*E^2)라고 알려져 있는데, 이분 매칭의 경우에는 이보다 더 빠르고 효율적으로 알고리즘을 설계할 수 있다.
그게 바로 단순히 DFS로 푸는 방법이다. (포드-풀커슨의 DFS가 아닌 그냥 DFS)

먼저 첫 출발로 문규가 네이버 클라우드를 선택한다. 현재까지는 네이버 클라우드가 아무에게도 선택되지 않았으므로 바로 선택할 수 있다.

문규의 선택이 끝났다면, 그 다음 경준님이 선택할 차례인데 경준님께서 희망하는 네이버 클라우드는 이미 문규가 선택하고 있는 상황이다.

이 때, 네이버 클라우드를 선택한 문규가 네이버 클라우드를 제외하고 다른 희망 기업을 선택할 수 있는지 살펴본다. 살펴보니 아직 카카오가 아무에게도 선택되지 않았으므로 카카오를 선택하였다.
그래서 경준님이 네이버 클라우드를, 문규가 카카오를 선택하게 되었다.

그 다음 윤주님이 기업을 선택할 차례가 왔다. 윤주님께서 희망하는 카카오는 또 문규가 선택하고 있는 상황이다.

이 때, 또 카카오를 선택한 문규가 카카오를 제외하고 다른 기업을 선택할 수 없는지 살펴본다. 네이버 클라우드를 혹시나 다시 한번 살펴 봤더니 경준님께서 계속 선택하고 계신 상황이라 선택할 수가 없었다.

그래서 카카오와 네이버 클라우드를 제외하고 남은 희망 기업중 남아있는 삼성전자를 선택하였다.

이렇게 문규는 삼성전자, 경준님은 네이버 클라우드, 윤주님은 카카오로 매칭되어 입사를 하게 되었다. 😊
시간복잡도
위와 같은 예시처럼 DFS를 이용해 이분 매칭을 간단히 풀 때 시간 복잡도는 O(V * E) 이다.
이 방법은 가장 빠른 속도의 알고리즘은 아니지만 구현이 가장 간단하고 쉽다는 점에서 많이 사용된다.
코드
이분 매칭에 대한 코드는 이분 매칭의 기본 문제라고 할 수 있는 열혈강호 : 백준 11375문제를 대표로 하여 작성하였다.
더 효과적인 이분 매칭 코드가 있지만, 일단 가장 간단하게 구현할 수 있는 DFS 풀이부터 숙지하도록 하자.
import java.io.*;
import java.util.*;
/*
* 회사에 N명의 직원과, M가지 작업이 있을 때,
* 해당 회사가 할 수 있는 최대 일의 개수를 구하시오.
*
* 1. 각 직원은 1개의 일을 할 수 있다.
* 2. 각 작업을 담당하는 사람은 1명이다. 즉, 1 : 1 매칭
* 3. 각 직원이 할 수 있는 일의 목록이 주어진다.
*
* 직원(집단 A)과 작업(집단 B)을 최대한 매칭시키는 베이직한 이분 매칭 문제.
*
* 메모리 시간
* 78212 964
*/
public class BaekOJ11375_배문규 {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StringBuilder sb = new StringBuilder();
static StringTokenizer st = null;
static final int MAX_SIZE = 1001;
static int N, M, worker[][], b[];
static boolean check[];
public static void main(String[] args) throws NumberFormatException, IOException {
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
worker = new int[N+1][];
for(int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine());
int cnt = Integer.parseInt(st.nextToken());
worker[i] = new int[cnt];
for(int j = 0; j < cnt; j++) worker[i][j] = Integer.parseInt(st.nextToken());
}
System.out.println(bMatch());
}
public static int bMatch() {
b = new int[MAX_SIZE]; // b배열의 인덱스 : 작업 인덱스, b배열의 값 : 직원 인덱스
check = new boolean[MAX_SIZE]; // 이미 확인한 직원인지 체크 배열
int result = 0; // 매칭된 작업 수
for(int i = 1; i <= N; i++) {
Arrays.fill(check, false); // 매번 매칭을 시도할 때마다 이미 매칭된 사람도
// 다른 작업으로 매칭이 바뀔 수 있으므로 방문 체크를 초기화 해야함
if(dfs(i)) result++; // i번 째 직원이 일과 매칭이 되면 카운트
}
return result;
}
public static boolean dfs(int workerIdx) {
if(check[workerIdx]) return false; // 이미 확인한 사람은 다시 확인할 필요 없음
check[workerIdx] = true;
// 해당 직원이 수행할 수 있는 작업들
for(int job : worker[workerIdx]) {
// 매칭이 가능한 경우는 2가지가 있다.
// 1. 아직 해당 작업이 아무런 직원과 매칭이 되어 있지 않았을 때
// 2. 이미 해당 작업에 매칭된 직원이 다른 작업도 매칭할 수 있을 때
if(b[job] == 0 || dfs(b[job])) {
b[job] = workerIdx; // 직원 <--> 작업 매칭하고 true 리턴
return true;
}
}
return false;
}
}