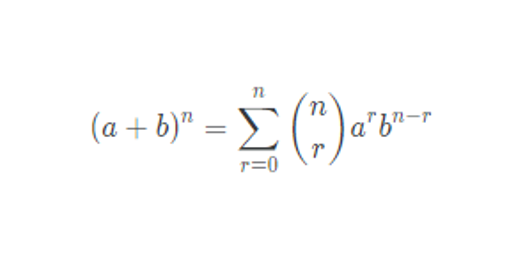이항 계수

우선 이항 계수를 다루기전에 근본적으로 이항 정리에 대해 알아야 한다.

이항 정리는 (A + B)^n (여기서 n은 음이 아닌 정수)라는 다항식을 전개할 때 쓰는 정리이며, 여기서 '이항'이라는 단어는 '두 개의 항'이라는 뜻이다.

이항 계수는 (A + B)^n 라는 다항식을 전개했을 때, A^r*B^(n-r) (0 <= r <= n인 정수)의 계수를 의미한다.

A^r*B^(n-r)의 계수는 총 n개의 문자를 순서없이 배열하는 경우의 수와 같으며, 이는 조합과 같다.

그래서 A^r*B^(n-r)의 계수는 nCr과 같다.

우리는 이항 계수의 수학적인 증명이나 성질을 자세하게 다루기보다는 PS에 이항 계수 관련 문제가 나오면

어떻게 이 이항 계수를 빠르고 효율적으로 구할 수 있느냐를 중점적으로 알아보려고 한다.

2가지 문제를 통해서 이항 계수 PS을 알아보도록 하자. 먼저 가장 기초적인 이항 계수를 구하는 문제이다.

자연수 N과 정수 K가 주어졌을 때, 이항 계수를 10,007으로 모듈라 연산한 값을 구하시오. (1 <= N <= 1,000 / 0 <= K <= N)

binomial_coefficient(N, K){
	K = Max(K, N-K); // K와 N-K 중 큰 수를 고른다. return으로  K를 나눈 값을 return하는데 K가 0일 수 있기 때문에
	A = N;
	
	for(i = K-1; i > 0; i--){
		A = A * (N - i); // nPk
		K = K * i;	// k!
	}
	
	return A/K; //nPk/k! == nCk
}

보통 위 같은 문제는 겉으로 보기에는 return 값이 엄청나게 커져 오버플로우가 발생할 수 있기 때문에 보기 편하게 10,007을 나눈 나머지 값을 구하라는 문제라고 생각할 수 있다.

그리고 실제로 N의 범위가 1,000까지기 때문에 정석적인 방식으로 이항계수를 구하고 모듈라 연산을 그냥 리턴할 때 하면 된다.

만약 N의 범위가 4,000,000이라면 위처럼 구할 수 있을까? 동일하게 자연수 N과 정수 K가 주어졌을 때, 이항 계수를 구하는 문제인데,

N의 범위를 4,000,000까지 확장하여 이항 계수를 1,000,000,007으로 모듈라 연산한 값을 구하여라.

이 땐 처음 문제와 다르게 모듈라 연산의 존재 유무가 중요해졌다.

이 문제를 풀기 위해서는 우리가 앞서 배운 모듈라 연산의 분배법칙 속성을 활용해야 한다.

N과 K의 이항계수는 nCk = N!/(K!*(N-K)!) 로 구할 수 있다.

그렇다면 이 이항계수를 모듈라 연산으로 분할정복해서 구할 순 없을까?

하지만 위에서 봤을 때, 덧셈, 뺄셈, 곱셈에 대해서는 분배법칙이 존재했지만, 나눗셈은 존재하지 않았다.

즉, (A / B) mod M != ((A mod M) / (B mod M)) mod M 이라는 것이다.

여기서 A를 N!, B를 K!*(N-K)! 이라고 대입해보자.

(N! / K!(N-K)!) mod M != ((N! mod M) / (K!(N-K)! mod M)) mod M 으로 바꿀 수 있다.

왜 성립하지도 않는데 귀찮게 대입을 해서 식을 직접 눈으로 확인해 본 이유가 있다.

우리가 이항 계수의 분수가 나눗셈이기 때문에 분배법칙이 적용되지 않았는데, 이 분수를 비틀어서 곱셈으로 만들어 버린다면 이항계수의 분배법칙을 가능하게 할 수 있다.

그렇다면 곱셈꼴로는 어떻게 만들까? 분수를 곱셈꼴로 만드는 방법은 역원을 이용하면 쉽게 만들 수 있다.

만약 A / B = C 라면, 이는 A * B^(-1) = C라는 의미이다. 즉 A 나누기 B는 A 곱하기 B의 역원과 같다.

그렇기 때문에, (N! / K!(N-K)!) mod M는 (N! (K!*(N-K)!)^(-1)) mod M 로 표현 가능하다.

역원을 이용해 나눗셈을 곱셈까지는 표현하는데는 성공하였다. 그런데 나눗셈이 존재했던 이유는 분수때문이고, 분수의 역원은 어쨌든 분수가 아닌가?

이 문제를 해결하기 위해서 필요한 공식이 '페르마의 소정리'이다.

페르마의 소정리는 다음과 같다.

A는 정수, P는 소수이며 A가 P로 나눠지지 않을 때, (A는 P의 배수가 아니라는 뜻)

A^P ≡ A (mod P)이다. (P에 대해 모듈라 합동이다 : P를 나눈 나머지가 같다.)

이는 이렇게 표현이 가능하다 -> A^P mod M ≡ A mod M

다시 말하지만 우리는 위 공식이 어떻게 증명되는지에 대해서는 관심없고 증명된 공식들을 잘 써먹는데에 관심이 있는 공학자들이다.

위 표현식을 다시 응용하면, A^(P-1) ≡ 1 (mod P) => A * A^(P-2) ≡ 1 (mod P)로 변형이 가능하다.

놀랍게도, A (mod P)에 대한 역원은 A^(P-2) (mod P)라는 것이다.

그렇다면 다시 문제로 돌아와서 해당 분수의 역원을 페르마의 소정리로 구해보면,

A는 (K! * (N-K)!) , P는 1,000,000,007 로 대입할 수 있다.

A^(-1) = A^(P-2) = (K! (N-K)!)^(-1) = (K! (N-K)!)^1,000,000,005 가 된다.

이제는 더 이상 역원이 분수가 아닌 정수로 표현되니, 모듈라 곱셈 분배 법칙 적용할 수 있게 되었다.

최종적으로 도출되는 식은 아래와 같다.

N! / (K!(N-K)!) mod M
= (N! (K!(N-K)!)^(-1)) mod M
= (N! (K!(N-K)!)^(M-2)) mod M
= ((N! mod M) (K! * (N-K)!)^(M-2) mod M) mod M

이렇게 정리가 된다.

이제 곱셈 분배법칙이 적용되니 분할 정복을 하여야 한다.

분할 정복은 (K! * (N-K)!)^(M-2)에서 지수 M-2를 계속 절반씩 나눠서 지수가 짝수일 때와 홀수일 때를 구분하여 리턴해주면 된다.

아래는 위 문제의 수도코드이다.

// 수도코드
M = 1,000,000,007
A = factorial(N); // N!
B = factorial(K) * factorial(N-K) % M; // K!*(N-K)!

print(A * divide_conquer(B, M-2) % M); // (N! * (K!*(N-K)!)^(M-2)) mod M  

// 팩토리얼 구하면서 mod M을 계속 해줌
factorial(num){
	result = 1;
	while(num > 1){
		result = (result * num--) % M
	}
	
	return result;
}

// num : 밑수, exp : 지수
divide_conquer(num, exp){
    	if(exp == 1) return num % M; // 지수가 1일 경우 num^1 이므로 num % M 리턴
    	
	temp = divide_conquer(num, exp/2); // 모듈라 연산 곱셈 분배법칙을 이용한 분할 정복
	
	if(exp % 2 == 1) return (temp * temp) * num % M; // 분할 정복이 끝나고 지수가 홀수가 남으면 ex)A^5 = A^2 * A^2 * A
	else return temp * temp % M; // 지수가 짝수면 A^4 = A^2 * A^2
}