빅오 표기법
- 시간 복잡도와 공간 복잡도는 주로 점근적 표기법 中 빅오 표기법을 이용하여 나타냄
- 최악의 경우에도 해당 알고리즘이 어떤 성능을 낼지 가늠해볼 수 있기 때문
알고리즘을 평가할 때 시간 복잡도와 공간 복잡도를 사용
시간 복잡도 (Time Complexity)
1. 정의
-
알고리즘의 수행시간을 평가
-
얼마나 빠른지
-
주의!
- 수행 시간은 실행환경에 따라 다르게 측정되기 때문에, 기본 연산의 실행 횟수로 수행 시간을 평가
2. 기본 연산
-
데이터 입출력 - copy, move...
-
산술 연산 - add, multiply ...
-
제어 연산 - if, while ...
3. 최선/최악/평균
-
최선의 경우 (Best Case)
-
빅 오메가 표기법 사용
-
최선의 시나리오로, 최소 이만한 시간이 걸림
-
-
최악의 경우 (Worst Case)
-
빅 오 표기법 사용
-
최악의 시나리오로, 아무리 오래 걸려도 이 시간보다 덜 걸림
-
알고리즘이 복잡해질수록 평균적인 경우는 구하기가 매우 어려워지기 때문에, 최악의 경우로 알고리즘의 성능을 파악
-
-
평균적인 경우 (Average Case)
-
빅 세타 표기법 사용
-
평균 시간을 나타냄
-
4. 계산법
1) 원리
-
연산 횟수가 다항식으로 표현될 경우, 최고차항을 제외한
모든 항과최고차항의 계수를 제외시켜 나타냄- 예시 1
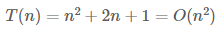
- 최고차항(n²)만 나타냄
- 예시 2
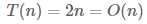
- 최고차항의 계수(2)는 제외함
참고
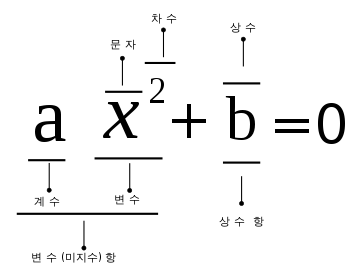
- 예시 1
2) 예시
int func (int n) {
int sum = 0; // 대입연산 1회
int i = 0; // 대입연산 1회
for(i=0; i < n; i++) { // 반복문 n+1회
sum += i; // 덧셈 연산 n회
}
for(i=0; i < n; i++) { // 반복문 n+1회
sum += i; // 덧셈 연산 n회
}
return sum; // 리턴 1회
}시간 복잡도 : T(n) = 4n + 5 = O(n)
5. 표기법
빅오 표기법을 사용해서 나타냄
O(1) - 상수 시간 (Constant time)
void func (int n) {
printf("%d\n", n);
}- 입력 크기(n)에 상관없이, 일정한 연산을 수행하면 시간복잡도는 O(1)
- 예시 : n에 상관없이 한 번에 연산만 수행하기 때문에 시간 복잡도는 O(1)
O(logN) - 로그 시간 (Logarithmic time)
for (i=1; i<=n; i*2) {
...
}- 입력 크기(N)가 커질 때, 연산 횟수가 logN에 비례해서 증가하면 시간 복잡도는 O(logN)
- 예시
- i 값이 반복할 때마다 2배씩 증가. 이것을 k번 반복했을 때
2의 k승 = N
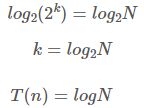
(k는 수행횟수) - 시간 복잡도는 logN
- i 값이 반복할 때마다 2배씩 증가. 이것을 k번 반복했을 때
- 예시
O(n) - 선형 시간 (Linear time)
for (i=0; i < n; i++) {
...
}- 입력 크기(n)가 커질 때, 연산 횟수가 n에 비례해서 증가하면 시간 복잡도는 O(n)
- 예시
- n만큼 반복문을 수행
- n에 값에 비례해서 연산수가 선형적으로 증가하기 때문에 시간 복잡도는 O(n)
- 예시
O(n²) - 2차 시간 (Quadratic time)
for (i=0; i < n; i++) {
for (j=0, j < n; j++) {
...
}
}- 입력 크기(n)가 커질 때, 연산 횟수가 n²에 비례해서 증가하면 시간 복잡도는 O(n²)
- 예시 : for문이 중첩되어 있기 때문에 n²에 비례해서 연산수가 증가
O(2ⁿ) - 지수 시간 (Exponential time)
int func (int n) {
if (n <= 1)
return n;
return func(n-1) + fun(n-2);
}- 입력 크기가 커질 때, 연산수가 2ⁿ에 비례해서 증가하면 시간 복잡도는 O(2ⁿ)
- 예시 : 한번 함수를 호출할 때마다 두 번씩 재귀로 함수를 호출하기 때문에 2ⁿ에 비례해서 연산수가 증가
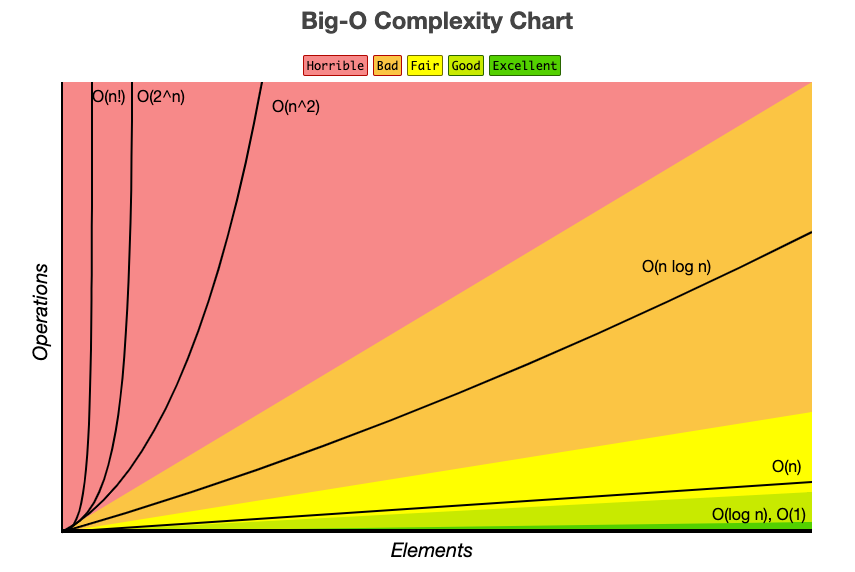
5가지 표기법 성능 비교
-
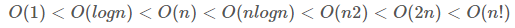
시간 복잡도 小(수행 시간 Short) <<< 시간 복잡도 大 (수행 시간 Long) -
n의 값이 작을 때는, 알고리즘 사이에 큰 차이가 없지만
n의 값이 커지면, 커질수록 복잡한 알고리즘은 수행 시간이 급격히 길어지게 됨
공간 복잡도 (Space Complexity)
1. 정의
-
알고리즘 수행에 필요한 메모리 양을 평가
-
메모리를 얼마나 잡아먹는지
-
보조공간(Auxiliary Space) + 입력 공간(input size)을 합친 포괄적인 개념
- 보조 공간(Auxiliary Space) : 알고리즘이 실행되는 동안 사용하는 임시 공간. 입력 공간을 고려하지 않음
2. 계산법
빅오 표기법을 사용해서 나타냄
int sum(int a[], int n) {
int x = 0;
for (int i = 0; i < n; i++) {
x = x + a[i];
}
return(x);
}4개의 변수를 사용하고 있음
-
int arr[n] : 4*n byte (입력 공간)
-
int n : 4 byte (입력 공간)
-
int x : 4 byte (보조 공간)
-
int i : 4 byte (보조 공간)
총 4n+12 에 메모리를 요구
메모리가 입력 값에 따라 선형적으로 증가하기 때문에 공간 복잡도는 O(n)
