정렬 알고리즘에 대한 것은 개발자 면접에서 자주 나오는 질문 중의 하나!
n개의 숫자를 입력할 때, 사용자가 지정한 기준에 맞게 정렬하여 출력하는 알고리즘
- 예시 : n개의 숫자가 저장된 배열이 있을 때, 오름차순 조건으로 작성 후 입력하면 오름차순 정렬된 배열이 출력됨
1. 선택 정렬 (Selection Sort)
1) 정의
-
정렬되지 않는 데이터들 中 가장 작은 데이터를 선택하여, 가장 앞부터 순서대로 정렬해나가는 알고리즘
-
현재 위치에 들어갈 값을 찾아 정렬하는 배열
-
최소 선택 정렬 (Min-Selection Sort)
- 현재 위치에 저장 될 값의 크기가 작을 경우
- 오름차순 정렬
-
최대 선택 정렬 (Max-Selection Sort)
- 현재 위치에 저장 될 값의 크기가 클 경우
- 내림차순 정렬
-
2) 사용 상황
데이터가 小 경우
구현은 쉬우나 처리 속도는 느리기 때문에, 데이터가 많은 경우에는 적합하지 X
3) 로직
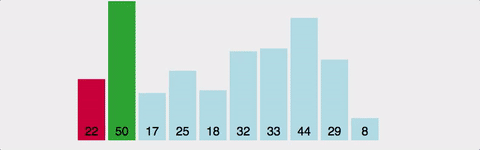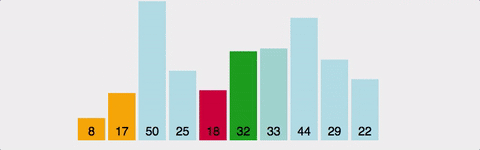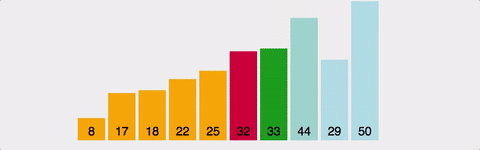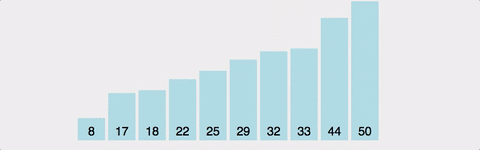
-
정렬되지 않은 인덱스에서 가장 앞에서부터 ~ 이후 배열값 中 가장 작은 값을 찾아간다.
-
가장 작은 값을 찾았다면, 그 값을 현재 인덱스의 값과 바꾼다.
-
다음 인덱스에서 위 과정을 반복한다.
4) 시간 복잡도
-
n-1개, n-2개, ... 이렇게 1개씩 비교를 반복한다.
전체 비교를 진행하므로, 시간 복잡도는O(N²) -
Worst, Average, Best 모두 동일
2. 삽입 정렬 (Insertion Sort)
1) 정의
- 현재 위치에서 그 이하의 배열들을 비교하여, 자신이 들어갈 위치를 찾아서 그 위치에 삽입
2) 사용 상황
데이터가 小 경우 or 일부가 정렬된 경우
실행 속도가 느리기 때문에, 데이터가 많은 경우에는 적합하지 X
그러나, 일부의 데이터들이 어느 정도 정렬(오름차순/내림차순)되어 있는 경우라면, 빠른 처리를 기대할 수는 있다.
3) 로직
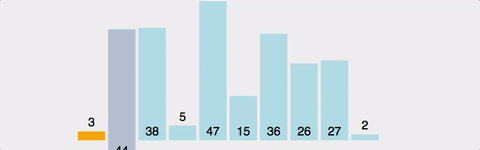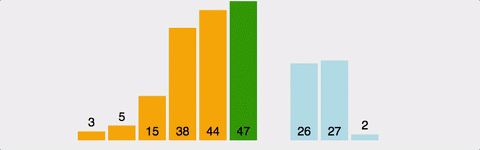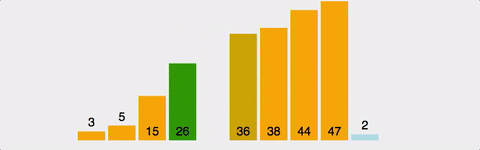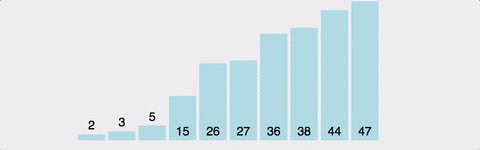
-
두 번째 인덱스부터 시작한다.
현재 인덱스는 별도의 변수에 저장하고,비교 인덱스를 현재 인덱스의 -1로 잡는다. -
별도로 저장해둔 삽입을 위한 변수 vs 비교 인덱스의 배열 값을 비교
-
삽입 변수 < 비교 인덱스의 배열 값 일 경우,
현재 인덱스로 비교 인덱스의 값을 저장하고, 비교 인덱스를 -1해서 비교를 반복삽입 변수 > 비교 인덱스의 배열 값 일 경우,
비교 인덱스 +1 에 삽입 변수를 저장
4) 시간 복잡도
-
시간복잡도는
O(N²)- 선택 정렬과 시간 복잡도가 동일하지만, 필요 시에 삽입하므로 연산 수는 더 小
즉, 더 효율적이다.
- 선택 정렬과 시간 복잡도가 동일하지만, 필요 시에 삽입하므로 연산 수는 더 小
-
Worst, Average는 동일
-
이미 정렬되어 있는 Best의 경우
O(N)
3. 버블 정렬 (Bubble Sort)
1) 정의
-
인접한 데이터를 교환 처리해서, 최종적으로는 모든 데이터들을 오름차순/내림차순 정렬하는 알고리즘
-
매번 연속된 두 개 인덱스를 비교해서, 정한 기준의 값을 뒤로 넘겨서 정렬
- 오름차순 정렬을 할 경우, 비교할 때마다 큰 값이 뒤로 이동한다.
- 결국 가장 큰 값은 가장 뒤에 저장된다.
2) 사용 상황
데이터가 小 경우
이해는 쉬우나 처리 속도는 느리기 때문에, 데이터가 많은 경우에는 적합하지 X
3) 로직
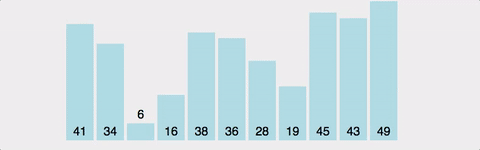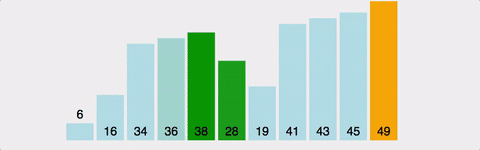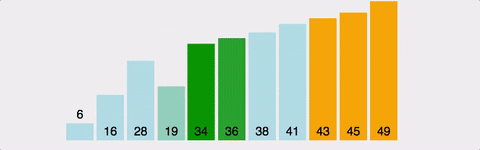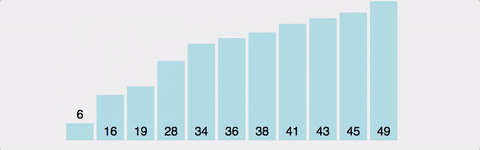
-
두 번째 인덱스부터 시작한다.
현재 인덱스 값 vs 바로 이전의 인덱스 값 비교 -
현재 인덱스 값 < 바로 이전의 인덱스 값 일 경우,
두 위치를 변경현재 인덱스 값 > 바로 이전의 인덱스 값
변경하지 않고, 다음 두 연속된 배열값들을 비교 -
이 과정을 '전체 배열의 크기 - 현재까지 순홚나 바퀴 수' 만큼 반복
4) 시간 복잡도
-
시간 복잡도는
O(N²)- 선택, 삽입 정렬과 시간 복잡도는 동일하지만, 연산 수가 많아서 가장 느리고 비효율적인 정렬
-
Worst, Average, Best 모두 동일
4. 합병 정렬 (Merge Sort, 병합 정렬)
1) 정의
- 분할 정복 (Divide and conquer) 방식으로 설계된 알고리즘
- 큰 문제를 반으로 분할해서 문제를 해결해나가는 방식
- 배열의 크기가 1보다 작거나 같을 때까지 분할을 반복
2) 로직
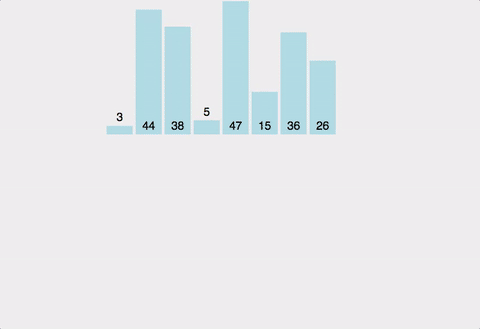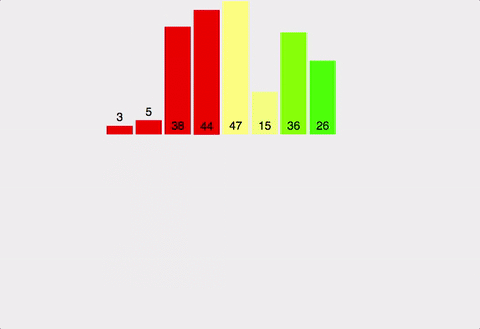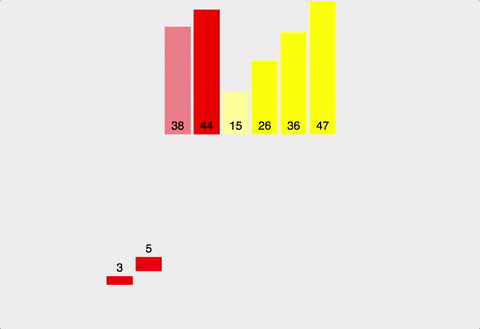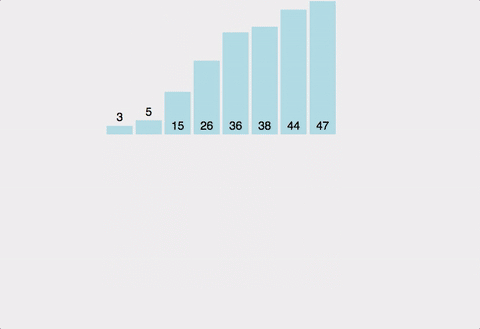
-
전체 배열을 반으로 나눈다.
- 배열의 시작/종료 위치를 입력 받아서, 둘을 더한 후 2를 나눠 그 위치를 기준으로 나눈다.
- 나눈 배열의 크기가 0 또는 1일 때까지 반복
-
두 배열 A, B 의 크기를 비교
- 각각 배열의 현재 인덱스를 i, j 로 가정해보자.
-
i 에는 A 배열의 시작 인덱스를 저장
j 에는 B 배열의 시작 주소를 저장 -
A[i] vs B[j] 비교
- 오름차순일 경우, 이 中 작은 값을 새로운 C 배열에 저장
- A[i] > B[j] 일 경우, A[i] 의 값을 C 배열에 저장 후, i 의 값을 +1 증가
-
이 과정을 i 또는 j 中 하나가 각자 배열의 끝에 도달할 때까지 반복
-
끝까지 저장하지 못한 배열의 값의 경우, 순서대로 모두 C 배열에 저장
-
C 배열을 원래 배열에 저장
3) 시간 복잡도
-
시간 복잡도는
O(N ㏒ N)- 장점 : 데이터를 정확히 반으로 나누고 정렬하기 때문에, 항상 일정한 시간 복잡도를 유지하므로 퀵 정렬의 한계점을 보완
- 단점 : (다른 알고리즘과 달리) O(n) 수준의 메모리가 추가로 필요
-
Worst, Average, Best 모두 동일
5. 퀵 정렬 (Quick Sort)
1) 정의
-
분할 정복 (Divide and conquer) 방식으로 설계된 알고리즘
- pivot point(피벗, 기준이 되는 값)을 설정해서,
이를 기준으로 작은 값은 왼쪽으로, 큰 값은 오른쪽으로 옮긴다 - 분할된 배열의 크기가 1일 때까지 반복
- pivot point(피벗, 기준이 되는 값)을 설정해서,
-
사용 빈도가 가장 多 알고리즘 유형
2) 사용 상황
데이터가 多 경우
처리 속도가 가장 빠른 알고리즘이기 때문 ("퀵" 정렬)
3) 로직
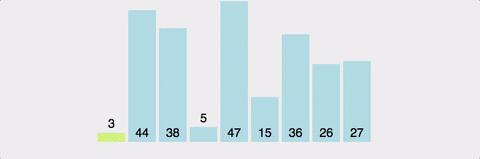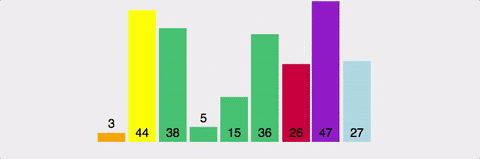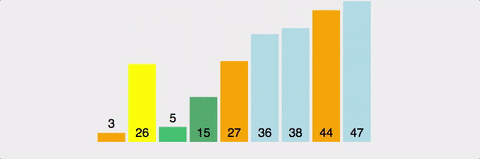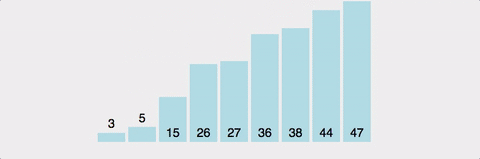
-
pivot point 로 설정할 배열의 값 하나를 정한다.
- 전체 배열 값 中 중간 값 or 랜덤 값으로 정함
-
left 변수와 right 변수를 생성
- left 변수 : 가장 왼쪽 배열의 인덱스를 저장
- right 변수 : 가장 오른쪽 배열의 인덱스를 저장
-
right 변수부터 비교를 진행
- left < right 일 경우에만 비교를 반복 진행
- pivot point < 비교한 배열 값 일 경우, right 를 -1 하고 비교를 반복
- pivot point 보다 작은 배열 값을 찾으면, 반복을 중지
-
left 변수 비교를 진행
- left < right 일 경우에만 비교를 반복 진행
- 비교한 배열 값 < pivot point 일 경우, left 를 +1 하고 비교를 반복
- pivot point 보다 큰 배열 값을 찾으면, 반복을 중지
-
left 인덱스 값과 right 인덱스 값을 바꾼다.
-
left < right 일 떄까지 위 과정을 반복
-
위 과정이 끝나면, left 값과 pivot point 를 바꾼다.
-
가장 왼쪽부터 ~ left-1까지, left+1부터 ~ 가장 오른쪽까지 로 나눠서 퀵 정렬을 반복
4) 시간 복잡도
-
시간 복잡도는
O(N ㏒ N)- 이미 정렬된 데이터일 경우, 비효율적
-
Average, Best는 동일
-
Worst의 경우
O(N²)
6. 힙 정렬 (Heap Sort)
1) 정의
-
이진트리 기반의 트리형 자료구조
-
최솟값 or 최댓값을 찾아내기 위해 사용
-
내림차순 정렬을 위해서는 최대 힙을 구성
오름차순 정렬을 위해서는 최소 힙을 구성
2) 로직
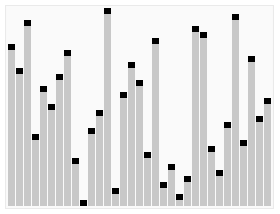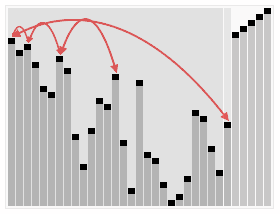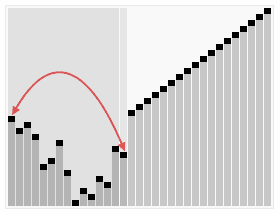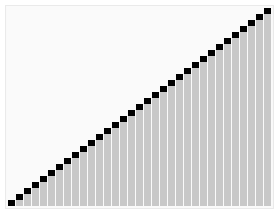
3) 시간 복잡도
-
시간 복잡도는
O(N ㏒ N) -
Worst, Average, Best 모두 동일
7. 기수 정렬 (Radix Sort)
1) 정의
-
기수 정렬은 낮은 자릿수(일의 자리 → 십의 자리 → 백의 자리 → ...)부터 비교하여 완성하는 정렬
- 장점 : 비교 연산을 하지 않으며 정렬 속도가 빠른 편
- 단점 : 데이터 전체 크기에 기수 테이블의 크기만 한 메모리가 더 필요
-
d 는 자릿수
2) 로직

3) 시간 복잡도
- 시간 복잡도는
O(dN)
참고: 기본 정렬 알고리즘(Sorting Algoritm) 요약 정리(선택, 삽입, 버블, 합병, 퀵)v1.1
[참고: 정렬 알고리즘 특징/종류/시간 복잡도 선택, 삽입, 버블, 합병, 힙, 퀵, 기수
참고: 정렬 알고리즘을 알아봅시다!!:)
