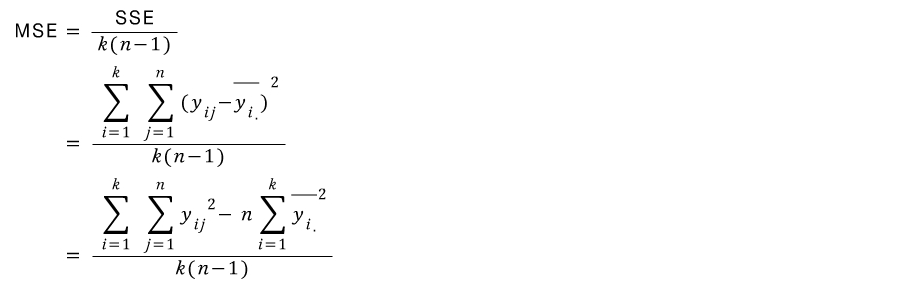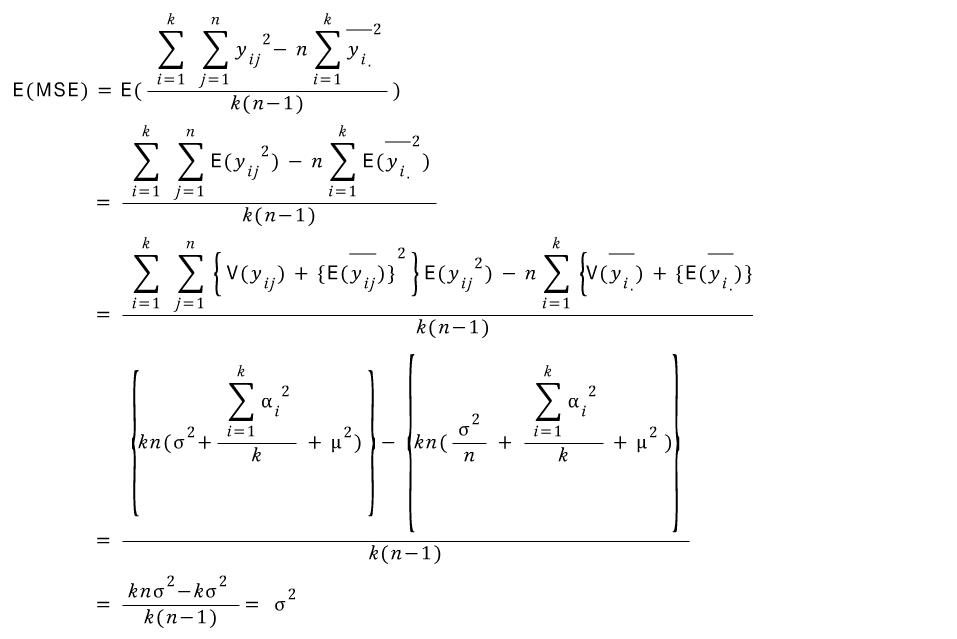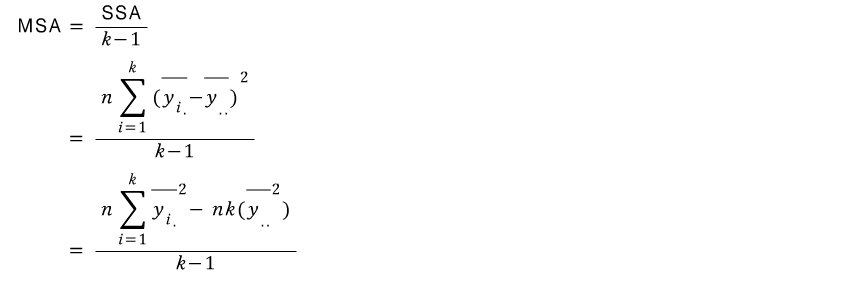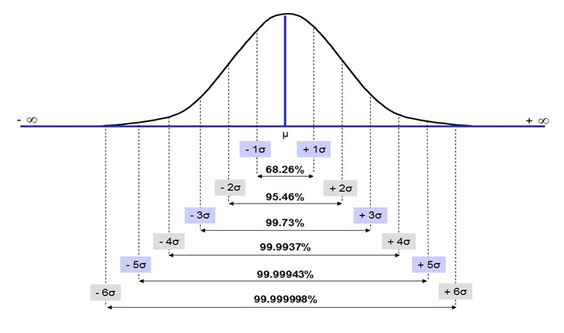
Comparing Several Populations

two populations: 두 집단에 대하여 알아볼 것이다.
모집단 1과모집단 2를 비교할 것이다.
3개의 집단에 대해서 모색을 해볼 것이다. 경우의 수는 3가지가 존재할 것이다.
Population 1,Population 2,Popluation 3가 있다고 가정해보면
총 3가지 경우의 수가 나온다. 즉
Population 1,Population 2
Population 2,Population 3
Population 1,Population 3
분산 분석이 3개 이상의Population을 비교하기 위한 한 방법론이 될 것이다.
Population(모집단)=>levels, treatments
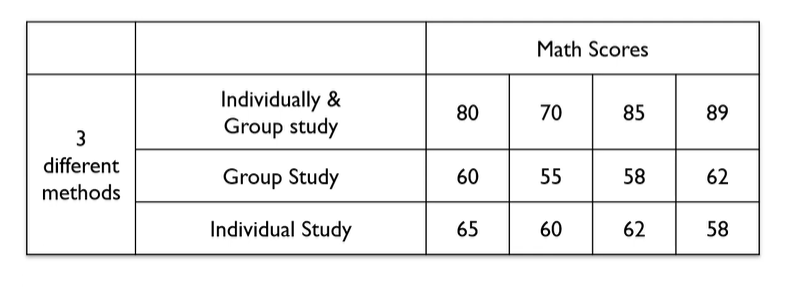
Example 1
The data show the Math's test from 3 different methods fo study. Conduct the hypothesis test stating that there is no difference of Math scores among 3 different methods of study.
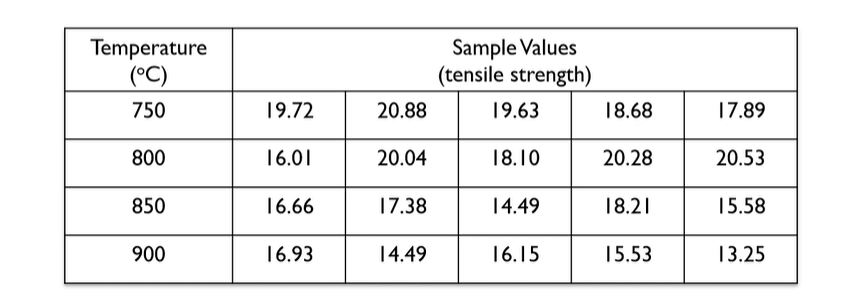
Example 2
An experiment was performed to determine whether the annealing temperature of ductile iron effects its tensile strength. Can you conclude that there are difference of tensile strength among 4 different temperature
annealing temperature : 담금질 온도
ductile iron : 연성철
tensile strength : 인장 강도
One-Way ANOVA Model


관측하는 값 (i번째 레벨에 j번째 관측치)
=> 평균 + 에러(에러는 정규분포를 따르고 있다.)

ANOVA에 대한 정의를 하라고 하면 위 slide대로 이야기하면 된다.'
귀무 가설, 대립 가설
Point Estimator
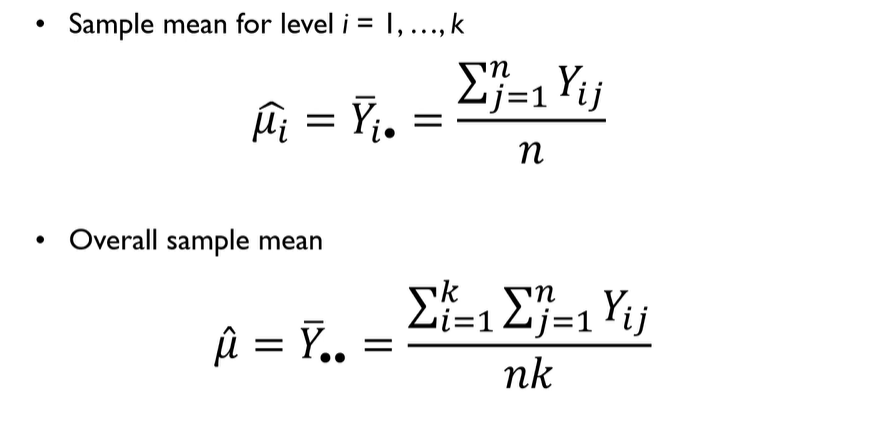
estimator=Yi dot(all)bar=
Sum of (i번째부터 j=1~whole observation) / n
overall mean=Yi dot dot bar(whole i, j)=
모든 i와 j에 대한 Sumation
k:level의 개수
n:Observation의 개수, 표본의 개수
One-Way ANOVA

Yij:i번째 레벨에서 j번째 관측치
y dot dot bar:전체 평균=Overall Mean
Yij-y dot dot bar
SST의 두번째 식을 더 많이 사용한다.
yi dot bar:i번째 level의 평균
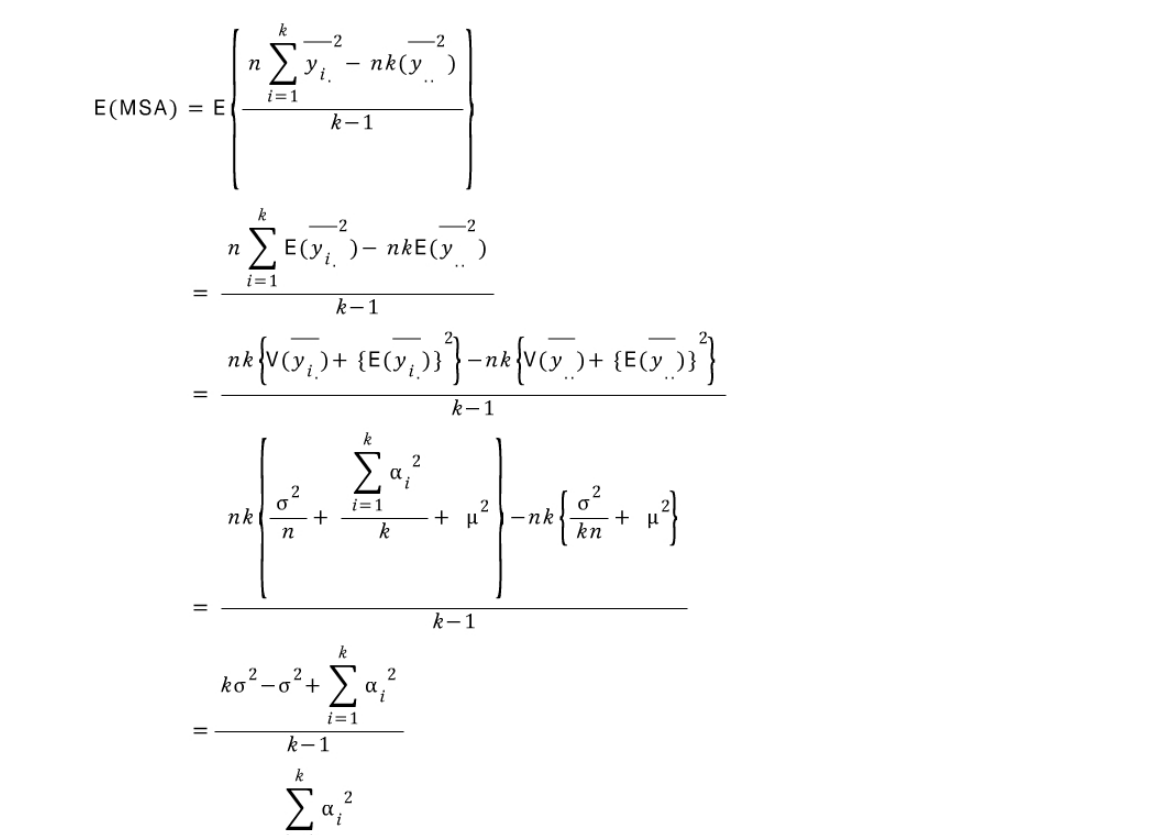
SSA:level 사이의 (level)간의 차이가 있는지

level 안에서의 평균
SSA:Between level
SSE:Within level
SSA>>SSE:different
SSE<SSE:difficult to say diffent
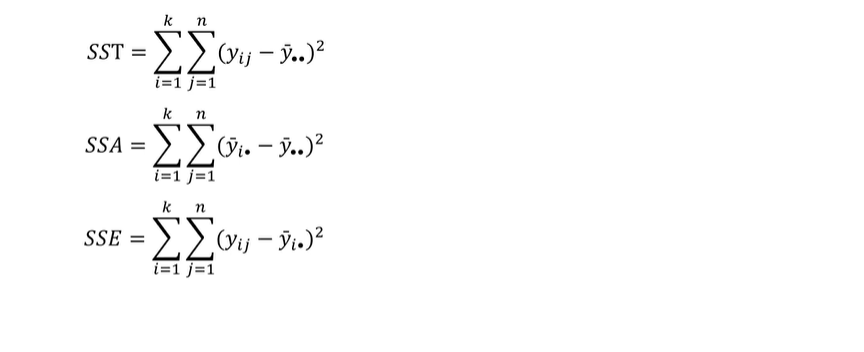
Variance formula(추가 설명)

결론적으로는
SSE,SSA,SST은카이제곱을 따른다
# Dispersion # 얼마나 데이터가 분산되어있는지 나타냄 # 분산 = Variance ########################################################### from typing import List Vector = List[float] # 사용 할 데이터 # num_friends = 유저의 친구 수 num_friends = [100.0,49,41,40,25,21,21,19,19,18,18,16,15,15,15,15,14,14,13,1 3,13,13,12,12,11,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10, 9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,8,8,8,8,8,8,8,8,8,8,8,8,8, 7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6, 6,6,6,6,6,6,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,4,4,4,4,4,4,4,4, 4,4,4,4,4,4,4,4,4,4,4,4,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3, 3,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1] # 데이터 평균 구하는 함수 def mean(xs: List[float]) -> float: return sum(xs) / len(xs) # 제곱합 공식 def sum_of_squares(v: Vector) -> float: """Returns v_1 * v_1 + ... + v_n * v_n""" return dot(v, v) # 백터의 내적 def dot(v: Vector, w: Vector) -> float: """Computes v_1 * w_1 + ... + v_n * w_n""" assert len(v) == len(w), "vectors must be same length" return sum(v_i * w_i for v_i, w_i in zip(v, w)) ########################################################### # "range" already means something in Python, so we'll use a different name # 데이터 범위를 구하는 함수 def data_range(xs: List[float]) -> float: return max(xs) - min(xs) assert data_range(num_friends) == 99 # 확인 # 편차를 구하는 함수 def de_mean(xs: List[float]) -> List[float]: """Translate xs by subtracting its mean (so the result has mean 0)""" x_bar = mean(xs) return [x - x_bar for x in xs] # 분산 구하는 함수 def variance(xs: List[float]) -> float: """Almost the average squared deviation from the mean""" # 분산에는 두개 이상의 요소가 필수 assert len(xs) >= 2, "variance requires at least two elements" #확인 n = len(xs) deviations = de_mean(xs) return sum_of_squares(deviations) / (n - 1) assert 81.54 < variance(num_friends) < 81.55 #확인

카이제곱 분포 v1(자유도)
카이제곱 분포 v2(자유도)
F:f분포를 따른다.f(자유도 v1, 자유도 v2)
numerator:분자
denominator:분모

n:관측치의 개수
k:level의 개수
F-test in ANOVA Table

MSA/MSE=MSA=SSA/k-|
MSE=SSE/k(n-|)
F*=검정통계량=MSA/MSE~f분포를 따른다
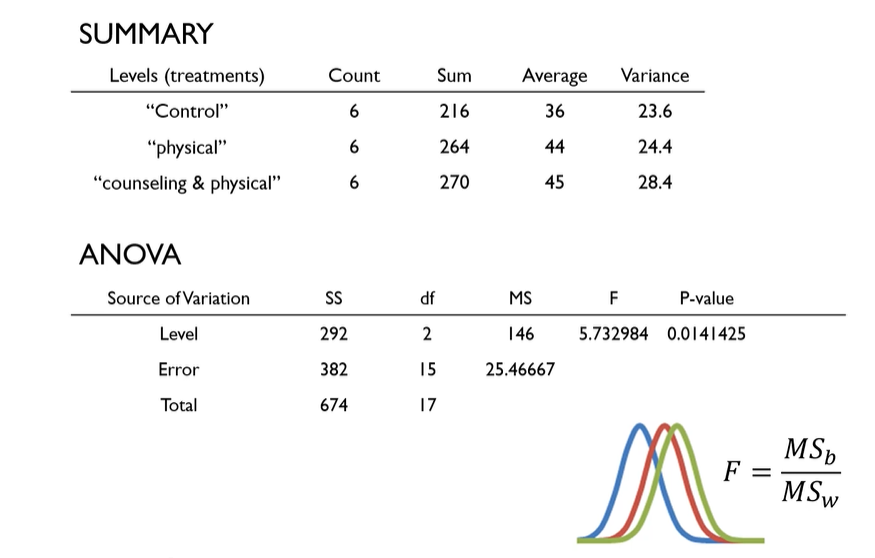
ANOVA Example : mobility
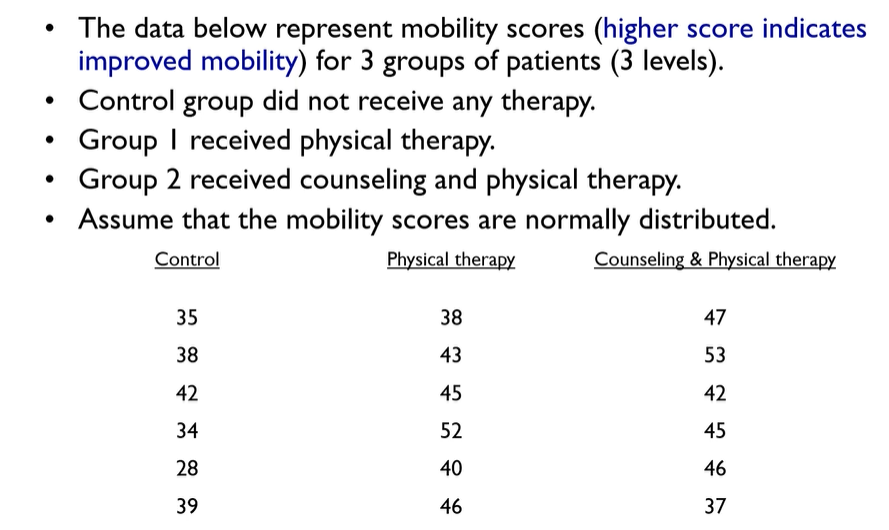

ANOVA will identify if at least two means are significantly different but will not identify which two (or more) means are different
Calculate Overall Mean and Levels Means

Y dot dot bar=Overall mean
Level means=Yi dot
Calculate the Within Sum of Squares : SSE(Within Level Variability)
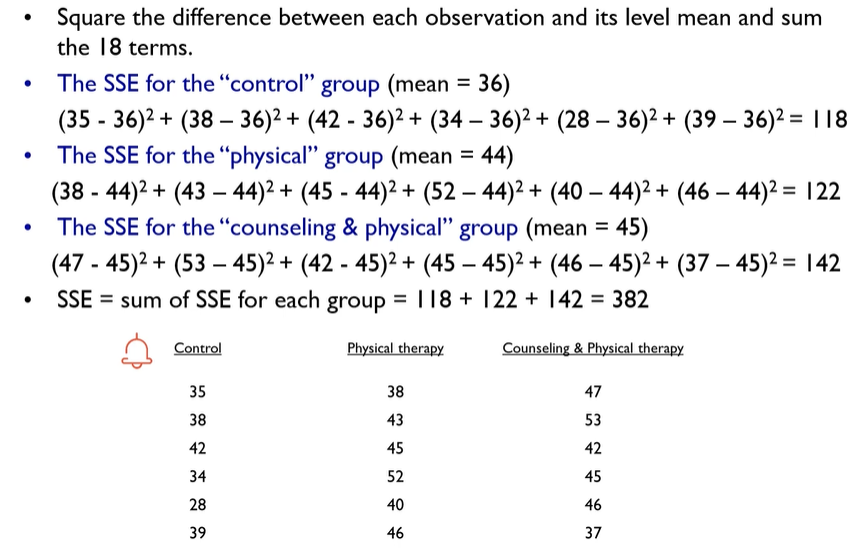
Calculate MSA and MSE

Calculate the ANOVA F-statistic
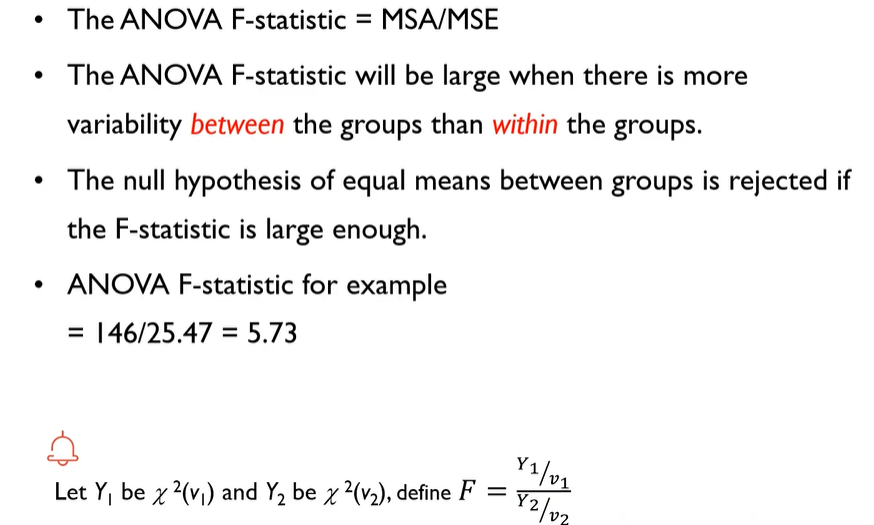
Distribution of ANOVA Test Statistic

p-value of the ANOVA Test

Decision about the Hypothesis

ANOVA Table for Mobility Data Example
Reference
Analysis of Variance(ANOVA; 분산 분석) by 김성범 교수 slide
https://blog.naver.com/PostView.naver?blogId=jokercsi1&logNo=222343020875
https://blog.naver.com/af472/220256046051