백준 | 골드 3 | 오등큰수 | Python

https://www.acmicpc.net/problem/17299

---

문제 파악

어제 푼 오큰수에 이어 오늘은 오등큰수 문제다.

길이 N의 수열 A가 주어지고, F(x)를 “수열 A에서 값 x가 등장한 횟수(빈도)”라고 할 때,

Ai의 오등큰수(NGF) = Ai의 오른쪽에 있으면서
F(Ai)보다 더 큰 빈도를 가진 수들 중 가장 왼쪽에 있는 값
(없으면 -1)

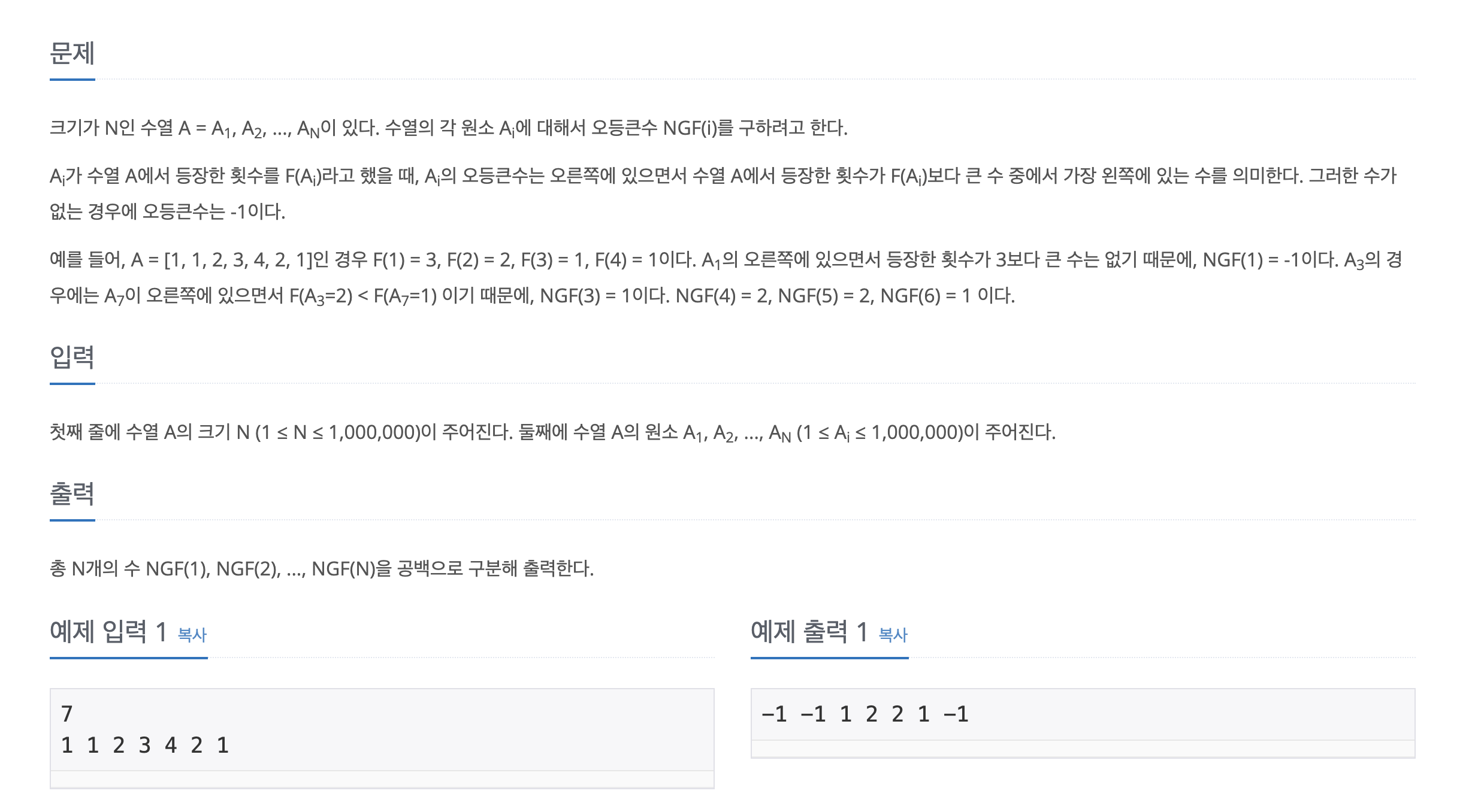
예) A = [1,1,2,3,4,2,1]
빈도: F(1)=3, F(2)=2, F(3)=1, F(4)=1

• A[0]=1, A[1]=1 → 오른쪽에 F(1)=3보다 더 큰 빈도를 가진 값이 없음 → -1
  • ✔️ 인사이트: “최빈값(빈도가 최대인 값)의 오등큰수는 항상 -1”
• A[2]=2(F=2) → 오른쪽에 F > 2인 값: 1(F=3)이 존재 → NGF[2]=1
• A[3]=3(F=1) → 오른쪽에 F > 1인 가장 가까운 값: 2(F=2) → NGF[3]=2
• … 이하 동일

---

“freq 배열로 바꿔서 오큰수로 풀면 되지 않을까?”

처음엔 이렇게 생각했다:

“A를 각 자리의 빈도로 바꾼 freq_A를 만들고,
거기에 오큰수를 돌리면 되지 않을까?”

예를 들어
A = [1,1,2,3,4,2,1] → freq_A = [3,3,2,1,1,2,3]

그리고 freq_A에 대해 “오큰수(숫자 크기 비교)”를 돌리면?

• 일부분은 우연히 맞지만, 정답 보장은 안 된다.

왜?
오등큰수는 값 그 자체가 아니라 ‘값의 빈도’를 비교한다.
freq_A로 바꿔버리면 원래 값 정보가 사라져서 결국 “큰 숫자”를 찾는 오큰수 문제가 된다.
즉, “빈도가 더 큰 값”을 찾아야 하는데, “빈도 숫자가 더 큰 수”를 찾는 문제로 변질된다.

결론: A는 그대로 두고, count[x] = F(x)만 따로 저장한 뒤
스택으로 순회하면서 count[A[i]]끼리 비교해야 한다.

---

핵심 아이디어 (O(N))

1. 빈도 전처리: count[x] = F(x)를 미리 계산
2. 스택: 인덱스를 담는 단조 스택 사용
   • 스택엔 “아직 오등큰수를 못 찾은 인덱스들”이 들어있다.
3. 오른쪽으로 한 번 훑으면서, 현재 i에 대해
   • 스택 top = j라 하면
     count[A[i]] > count[A[j]] 이면 → NGF[j] = A[i] (j의 오등큰수 발견)
     발견될 때까지 pop
   • 이후 i를 스택에 push
4. 끝까지 가면 스택에 남은 애들은 전부 -1

오큰수(값 비교)와 같은 패턴인데, 값 비교 대신 count[값] 비교만 한다는 점이 포인트.

---

해답 및 풀이

import sys
input = sys.stdin.readline

N = int(input())
A = list(map(int,input().split()))

# 빈도수 리스트 제작
if A:
    max_val = max(A)
else:
    max_val = 0

count = [0] * (max_val+1)
for x in A:
    count[x] += 1

NGF = [-1] * N
stack = []

for i in range(N):
    while stack and count[A[i]] > count[A[stack[-1]]]:
        j = stack.pop()
        NGF[j] = A[i]
    stack.append(i)

print(*NGF)

---

오큰수 문제와 완전히 동일한 문제였다.
그저 빈도 횟수를 리스트로 전처리해주는 로직만 더 하면 되었었다.

A에서 가장 큰 val 인 max_val를 찾고,
크기가 max_val + 1 인 count 리스트 만들어주고
A순회하며 count에 횟수 넣어주며 빈도횟수 리스트를 만드는 법을 기억하자.