백준 | 플래티넘 5 | 히스토그램 | Python

https://www.acmicpc.net/problem/1725

---

문제 파악

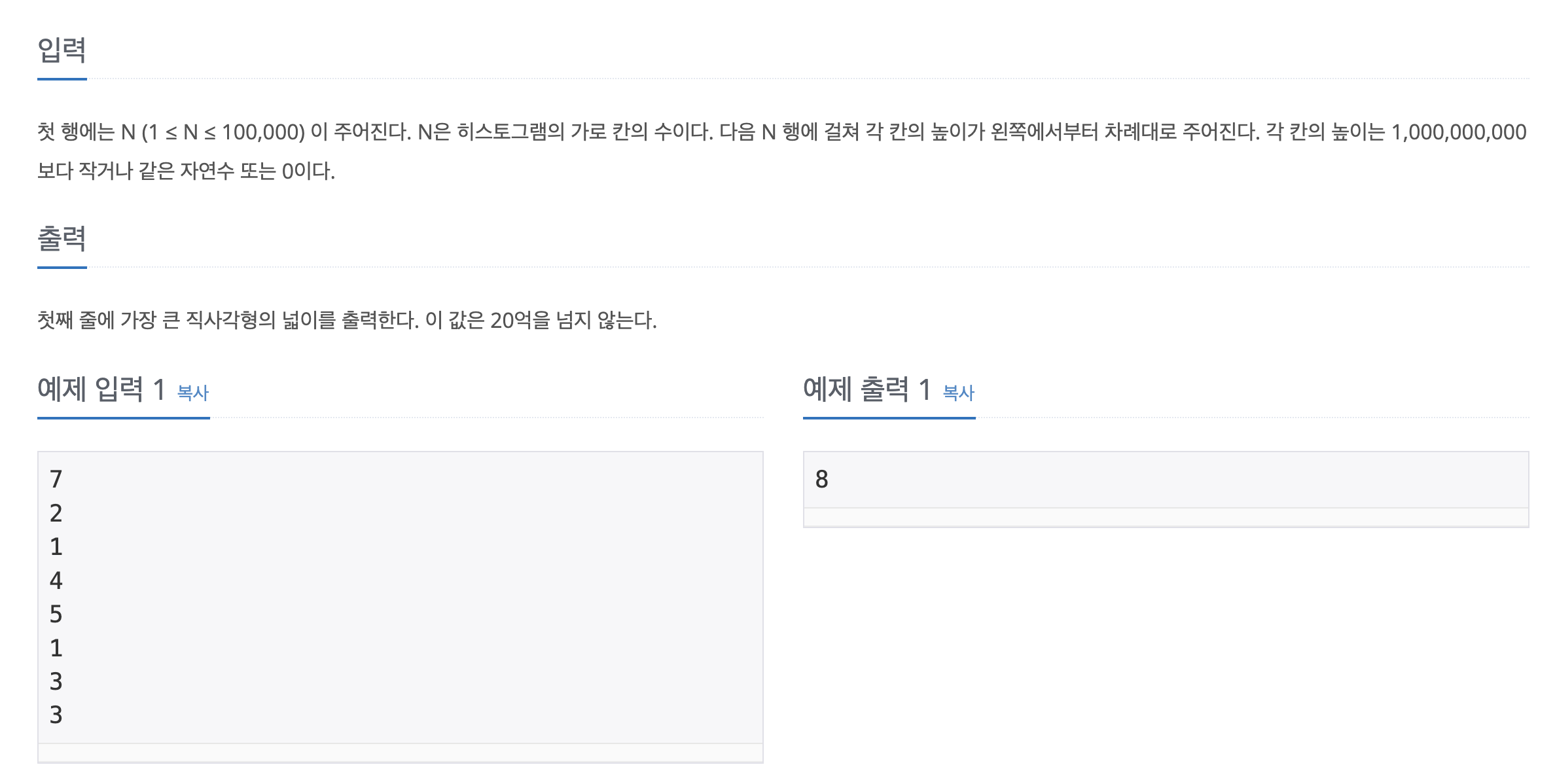
가로 폭이 1로 동일한 막대그래프 높이 N개가 주어진다.
이때 히스토그램 안에서 만들 수 있는 가장 넓은 직사각형의 넓이를 구하면 된다.

---

내 첫 시도(오른쪽만 카운팅)와 한계

처음엔 이렇게 생각했다:

• 각 시작점에서 오른쪽으로만 가면서 “시작 높이 이상”인 막대를 카운팅
• 작아지는 순간 시작높이 * 카운트로 넓이 계산

하지만 이렇게 하면 왼쪽으로 확장되는 폭을 놓친다.
예) [6, 5, 6]에서 높이 5는 왼쪽의 6도 포함해서 [6,5,6] 전체 폭 3을 쓸 수 있다 → 면적 15(정답).
오른쪽만 보며 세면 폭 2(=10)만 계산되어 최대값을 놓침.
또, 모든 시작점에서 양쪽을 확장하면 최악 O(N²)가 된다.

---

정답 접근: 단조 증가 스택 + 센티넬(0)

핵심 아이디어:

• 인덱스를 담는 스택을 유지하되, 스택에 담긴 막대 높이가 단조 증가(=오름) 하도록 유지한다.
• 현재 막대 높이 h가 스택 top의 높이보다 작아지는 순간,
  top 막대는 더 확장할 수 없으므로 그 막대의 직사각형 면적을 확정한다.
• 이때 폭(width)은
  • 스택이 비었으면: 왼쪽 끝까지 쭉 가능 ⇒ width = i
  • 스택이 비어있지 않으면: 새 top의 오른쪽부터 현재 i-1까지 가능 ⇒ width = i - stack[-1] - 1
• 마지막까지 남은 막대들도 계산되도록, 뒤에 센티넬(0) 을 하나 붙여서 자동으로 비우게 한다.

---

해답 및 풀이

    import sys
    input = sys.stdin.readline

    N = int(input())
    heights = [int(input()) for _ in range(N)]

    #  끝에 0 추가 → 마지막에 스택을 자연스럽게 모두 비움
    heights.append(0)

    stack = []      # 높이가 아니라 '인덱스'를 저장
    max_area = 0

    for i, h in enumerate(heights):
        # 현재 높이가 top의 높이보다 낮아지면, top 막대의 면적을 확정
        while stack and heights[stack[-1]] > h:
            top = stack.pop()
            height = heights[top]
            # 왼쪽 경계: (새 top) + 1, 오른쪽 경계: i - 1
            width = i if not stack else i - stack[-1] - 1
            max_area = max(max_area, height * width)
        stack.append(i)

    print(max_area)

• 시간 복잡도: O(N) (각 인덱스가 push/pop 최대 한 번씩)
• 공간 복잡도: O(N) (스택)

---

예제 [1,4,5,4] 흐름

heights = [1, 4, 5, 4, 0]   # (0은 센티넬)
stack = []
max_area = 0

-----------------------------------
i=0, h=1
- stack 비어있음 → stack.append(0)
stack = [0]

-----------------------------------
i=1, h=4
- top=0 → H[0]=1 ≤ 4 → while문 통과
- stack.append(1)
stack = [0, 1]

-----------------------------------
i=2, h=5
- top=1 → H[1]=4 ≤ 5 → while문 통과
- stack.append(2)
stack = [0, 1, 2]

-----------------------------------
i=3, h=4
- top=2 → H[2]=5 > 4 → while문 진입
	top = stack.pop() 2가 top됨
    height = heights[2] = 5
    width = stack이 비어있지 않으므로 i - stack[-1] - 1 
    width = 3 - 1 - 1 = 1
    area = width * height = 5 * 1 = 5 → max_area = 5
    
- top=1 → H[1]=4 ≤ 4 → while문 stop
- stack.append(3)
stack = [0, 1, 3]

-----------------------------------
i=4, h=0 (센티넬)
- top=3 → H[3]=4 > 0 → pop 3
    height = 4
    width = 4 - 1 - 1 = 2
    area = 8 → max_area = 8
    
- top=1 → H[1]=4 > 0 → pop 1
    height = 4
    width = 4 - 0 - 1 = 3
    area = 12 → max_area = 12
    
- top=0 → H[0]=1 > 0 → pop 0
    height = 1
    stack 비었음 → width = i = 4
    area = 4 → max_area = 12
- push 4
stack = [4]

-----------------------------------
끝
max_area = 12