---

문제 파악

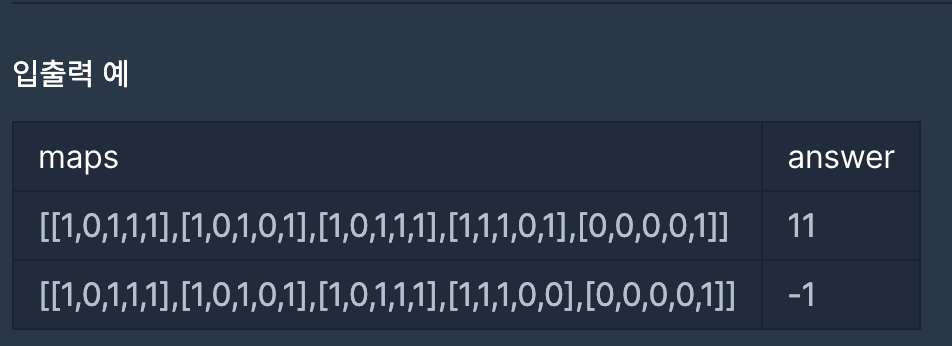
2차원 격자 maps가 주어진다.

1 : 이동 가능 (길)
0 : 이동 불가능 (벽)

좌상단 (1,1)에서 우하단 (n,m)까지 최단거리(칸 수)를 구해서 반환,
도착할 수 없다면 -1이 반환되어야 하는 핵심은 간단한 문제이다.

가중치가 없고 상하좌우 벡터를 만들어 BFS로 푸는 기본적인 BFS 문제이다.

해답 및 풀이

from collections import deque

# maps의 (1,1) -> (n,m) 까지 최단거리 return
# BFS 기본문제
def solution(maps):
    dx = [-1,1,0,0]
    dy = [0,0,-1,1]
    
    # maps, 0은 벽이 있는 자리, 1은 벽이 없는 자리
    # [[1,0,1,1,1],
    # [1,0,1,0,1],
    # [1,0,1,1,1],
    # [1,1,1,0,1],
    # [0,0,0,0,1]]

    N = len(maps[0]) # 가로
    M = len(maps) # 세로
    
    visited = [
        [-1 for _ in range(N)] for _ in range(M)
    ]
    
    queue = deque()
    queue.append((0,0))
    visited[0][0] = 1
    
    while queue:
        y, x = queue.popleft()
        
        for d in range(4):
            ny = y + dy[d]
            nx = x + dx[d]
            
            if 0 <= ny < M and 0 <= nx < N and maps[ny][nx] == 1 and visited[ny][nx] == -1:
                visited[ny][nx] = visited[y][x] + 1
                queue.append((ny,nx))
        
    
    return visited[M-1][N-1]

---

방향 벡터 dx, dy 선언해주고,
visited 배열 만들어준 후
deque() 큐 자료구조에 시작 좌표 넣구
시작 좌표 방문 처리( + 거리) 해준 후
y, x 잘 뒤집어서 써주고
범위 잘 확인해주고 visited[ny][nx] = visited[y][x] + 1 로 거리를 1씩 늘려주면 되는
기본적인 상하좌우 탐색 BFS 최단거리 문제였지만,
백준이 아닌 프로그래머스 환경에서 입력값이 주어진 채로 구현하려니 조금 어색했다.